zAB= NANBπ![]()
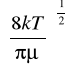
[s-1 m-3]
II Teoria zderzeń aktywnych
Teoria zderzeń aktywnych wyjaśnia postać równania Arrheniusa czyli:
co oznacza czynnik przedwykładniczy w tym równaniu,
jaki związek zachodzi między energią aktywacji a mechanizmem reakcji i jak stała szybkości zależy wykładniczo od tej energii oraz od temperatury.
Rozważamy jednorodne reakcje dwucząsteczkowe przebiegające w fazie gazowej.
Założenia tej teorii:
reakcja między dwiema cząsteczkami może zajść tylko w momencie ich zderzenia się,
suma energii zderzających się cząsteczek przypadająca na określone stopnie swobody ich ruchu musi być większa od wartości progowej,
cząsteczki traktujemy jako sztywne kule.
Dla reakcji: A + B → produkty ,
wychodząc ze wzoru na całkowitą liczbę zderzeń między cząsteczkami A i B
zAB= NANBπ![]()
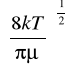
[s-1 m-3]
oraz wyrażenia na energię
![]()
to
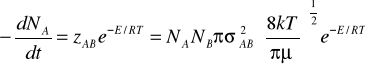
Jeżeli szybkość reakcji
r = 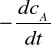
![]()
to liczba cząsteczek w 1 cm![]()
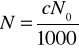
, → 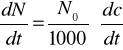
czyli
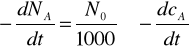
Przekształcając powyższe równanie i podstawiając wyrażenie -dNA/dt
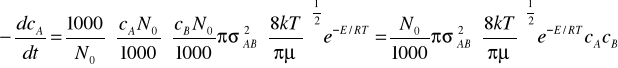
stwierdzamy, że szybkość elementarnej reakcji dwucząsteczkowej jest proporcjonalna do iloczynu stężeń substratów.
Stała szybkości jest zależna od temperatury:
![]()
po zlogarytmowaniu i zróżniczkowaniu względem T
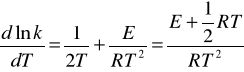
Teorię zderzeń aktywnych uzupełnia dodatkowa hipoteza, która mówi: aby zderzające się cząsteczki uległy reakcji, muszą mieć oprócz dostatecznej energii odpowiednią wzajemną orientację przestrzenną w momencie zderzenia. A więc prawa strona równania musi być pomnożona przez współczynnik steryczny P.
![]()
, gdzie ![]()