ZADANIA Z ANALIZY MATEMATYCZNEJ (2)

1. Zbadać monotoniczność ciągów:

a)
n  b)
n ; c)
n

d)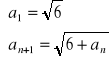
n ≥ 

2.Korzystając z definicji granicy ciągu liczbowego wykazać, że:

a)
b)
c)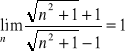

3.Korzystając z odpowiednich granic i twierdzeń obliczyć lim

, jeżeli wyraz ogólny ma postać:

a)
b)

c)
d)

e)
f)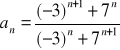
g)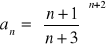

h)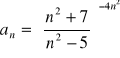
i)
j)

k)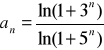
l)
m*)

n*)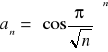
o)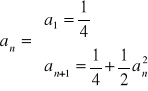
n

4.Obliczyć
,
, jeżeli:

a)
b)
c)

d)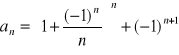
e)

f)

---