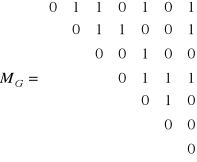Kolorowanie grafów: pokolorowanie wierzchołków jak najmniejszą liczbą kolorów tak, by żadne dwa wierzchołki połączone krawędzią nie miały tego samego koloru.

Algorytm sekwencyjny:

1. Ustalić listę kolorów

2. Dla każdego wierzchołka: wrócić do początku listy kolorów i pomalować kolorem o jak najmniejszym numerze, którym ten wierzchołek może być pomalowany.

Inna heurystyka:

Algorytm:

1. Za Z przyjąć zbiór pusty, Do Grafu G zastosować PROCEDURA(G)

2. PROCEDURA(G)

3. Pokolorować Z kolejnym kolorem z listy (zaczynamy od początku listy)

4. Zredukować G o Z i krawędzie z nimi związane.

5. Jeśli G niepusty, krok 1, w przeciwnym przypadku STOP

PROCEDURA(G)

1. G1:=G

2. W G1 znaleźć wierzchołek o minimalnym stopniu (liczba krawędzi wychodzących z wierzchołka), jeśli więcej, wybrać dowolny.

3. Z poszerzyć o wybrany wierzchołek

4. Zredukować G1 o wybrany wierzchołek, jego bezpośrednich sąsiadów i związane z nimi krawędzie

5. Jeśli G1 niepusty, krok 2. W przeciwnym przypadku STOP

Planowanie: Egzaminy dla przedmiotów E1, E2, E3, E4, E5, E6, E7 , 5 dni. Macierz pokazuje, w których parach egzaminów uczestniczy przynajmniej jeden student