Wyznaczanie modułu sztywności metodą dynamiczną.

W doświadczeniu tym potrzebne nam będą następujące przedmioty: drut umocowany w uchwycie, wibrator, obciążniki, suwmiarka, śruba mikrometryczna, waga oraz stoper.

Do jego przeprowadzenia powinniśmy znać poniższe pojęcia oraz prawa:

• Naprężenie styczne - to stosunek siły stycznej F_s do powierzchni S, na którą ona działa. Wyraża się ono następującym wzorem:

.

• Naprężenie normalne - jest to stusunek siły (odkształcającej) prostopadłej do powierzchni (F_n) do wielkości powierzchni S, na którą działa:

.

• Rodzaje odkształceń - wyróżniamy następujące typy: odkształcenie sprężyste (znika po odjęciu działającej siły zewnętrznej), odkształcenie plastyczne (po odjęciu siły nie znika - następuje trwała deformacja), odkształcenie typu skręcania lub ścinania (typy odkształcenia plastycznego - następuje zachwiana równowaga sił międzyatomowych).

• Prawo Hooke'a - wyraża proporcjonalność naprężenia i odkształcenia i w przypadku działania naprężeń stycznych przyjmuje postać:

,

gdzie: G - moduł sztywności o wymiarze [Nm^-2rad^-1], natomiast φ to miara deformacji kątowej.

• Moduł sztywności (skręcenia) wyraża się następującym wzorem:

'

gdzie l - długość drutu, r - promień drutu, T - okres drgań wibratora nieobciążonego lub wstępnie obciążonego, T₁ - okres drgań wibratora obciążonego znanymi masami, I₁ - dodatkowy moment bezwładności, który wyrażamy wzorem:

,

gdzie d to odległość osi walców od wibratora, N to ilość walców, m to ich masa, a I₀ to moment bezwładności pojedynczego walca względem jego osi symetrii. Dla walca o promieniu R: I₀ = (1/2)mR².

Pomiary i obliczenia:

Długość drutu (l)			1640,0 [mm]
Średnica obciążników (2R)			32,1 [mm]
Masa obciążników (m)			94,0 [g]
l.p.		Średnica drutu (2r)
1		1,03 [mm]
2		1,07 [mm]
3		1,04 [mm]
4		1,02 [mm]
5		1,02 [mm]
6		1,03 [mm]
7		1,02 [mm]
8		1,04 [mm]
9		1,03 [mm]
10		1,02 [mm]

Z powyższych informacji możemy wyliczyć promień obciążników, który wynosić będzie R = 16,05 [mm].

Przeciętna średnica drutu: 2r = 1,032 [mm]

Odchylenie standardowe wynosi σ = 0,015 [mm], co stanowi ok. 1,5% całej wartości - czyli wynik jest dość dokładny.

Przyjmujemy, iż średnica drutu wynosi: 2r = 1,032 ± 0,015 [mm]. Tak więc możemy założyć, iż wartość promienia drutu to r = 0,502 ± 0,008 [mm].

Położenie obciążników	Czas 10 T [s]	Czas T [s]
brak	41,94	4,19
dA	50,40	5,04
dB	68,63	6,86
dC	91,34	9,13

Odległości kołków od środka wibratora:

d_A = 50,0 [mm]

d_B = 100,0 [mm]

d_C = 150,0 [mm]

Błędy pomiaru:

Δr = ± 0,01 [mm]

Δl = ± 0,1 [cm] = ± 1,00 [mm]

ΔR = ± 0,10 [mm]

Δd = ± 1,0 [cm] = ± 10,00 [mm]

Δm = ± 0,1 [g]

ΔT = ΔT₁ = ± 0,1 [s]

Błędy:

1. Błąd pomiaru momentu bezwładności dla pojedynczego walca:

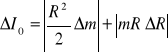
2. Błąd pomiaru całkowitego momentu bezwładności (dla walców w odległości d):

3. Błąd wyznaczania modułu sprężystości:

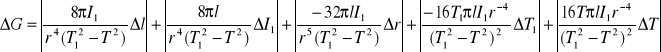
I₀ = (1/2)*94,0*10^-3*(32,1/2*10^-3)²=12,107*10^-6

dla d_A:

I_1A = 4 · 12,107 · 10^-6 + 4 · 94,0 ·10^-3 · (50,0 · 10^-3)² = 0,99 · 10^-3

dla d_B:

I_1B = 4 · 12,107 · 10^-6 + 4 · 94,0 ·10^-3 · (100,0 · 10^-3)² = 3,81 · 10^-3

dla d_C:

I_1C = 4 · 12107 · 10^-9 + 4 · 94,0 ·10^-3 · (150,0 · 10^-3)² = 8,51 · 10^-3

Położenie obciążników	G [Nm^-1rad^-1]
dA	8,19 · 10^10
dB	8,38 · 10^10
dC	8,40 · 10^10

Średnia wartość modułu sztywności wyniosła: 8,32 · 10¹⁰ [Nm^-1rad^-1].

Wnioski:

Po wyliczeniu średniej wartości modułu sztywności zakładamy pewną niedokładność w obliczeniach - odczytując wartości tablicowe - możemy wywnioskować, iż metalem z którego wykonany był badany przez nas drut - była stal, której tablicowa wartość wynosi 8,15 · 10¹⁰ [Nm^-1rad^-1], czyli niewiele odbiega od tego, co doświadczalnie zbadaliśmy. Można przyjąć, że powyższe zadanie zostało przeprowadzone w sposób poprawny.

---