POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI FILIA w JELENIEJ GÓRZE |
SPRAWOZDANIE Z ĆWICZENIA NR 9 TEMAT: Wyznaczanie momentu bezwładności brył metodą Wahadła torsyjnego.
|
||||
Imię i nazwisko:
|
Numer kolejny ćwiczenia
4 |
Zaliczenie |
|||
Grupa
3 |
Wydział
E-ka |
Rok
I |
Data wykonania ćwiczenia
18 marca 1999 |
|
|
WSTĘP TEORETYCZNY.
Wahadłem nazywamy bryłę sztywną, która pod działaniem przyłożonych sił wykonuje ruch drgający wokół nieruchomego punktu lub osi. W naszym doświadczeniu do wyznaczenia momentu bezwładności brył posłużymy się wahadłem torsyjnym. Jest to ciało sztywne, umocowane do drutu i wykonujące ruch drgający wokół osi pionowej pod działaniem momentu sił odkształconego sprężyście (skręconego) drutu.
Po wychyleniu wahadła o kąt α pojawi się moment siły zawracający wahadło do położenia równowagi. Jest to moment sił sprężystych przeciwstawiających się odkształceniu drutu (jego skręcaniu ). Dla małych kątów wychyleń M.= -Dα , gdzie D- moment kierujący sił sprężystych. Jeżeli na ciało mogące wykonywać tylko ruchy obrotowe wokół ustalonej osi działa moment siły M. Wprost proporcjonalny do kąta wychylenia α z położenia równowagi trwałej, a zwrócony zawsze tak, aby temu wychyleniu przeciwdziałać, to ciało będzie pod jego wpływem wykonywało obrotowe drgania harmoniczne.
Zgodnie z drugą zasadą dynamiki ruchu obrotowego ( M=Iε )
![]()
Podstawiając do powyższego równania moment siły dany wzorem M= -Dα otrzymujemy różniczkowe równanie ruchu wahadła w postaci:
![]()
Rozwiązaniem tego równania jest funkcja :
![]()
Największe wychylenie wahadła z położenia równowagi α=α0 nazywamy amplitudą drgań. Wielkość ψ=ωt+ϕ nazywamy fazą drgań, ϕ jest fazą początkową (fazą w chwili rozpoczęcia pomiaru czasu).
![]()
Równanie:
Jest kinematycznym równaniem ruchu drgającego harmonicznego. Prędkość kątową wahadła drgającego harmonicznie uzyskujemy obliczając pochodną, względem czasu, wychylenia:
![]()
Stan ruchu wahadła określony jest wychyleniem z położenia równowagi i prędkością kątową. Okresem drgań nazywamy czas T, po którym stan ruchu się powtarza. Żądamy zatem, aby wychylenie α i prędkość kątowa dα /dt wahadła miały po czasie T znowu takie same wartości. Ponieważ okresem funkcji trygonometrycznych sinus i cosinus jest kąt 2π , więc zgodnie z definicją, okres drgań spełnia zależność:
![]()
Stąd wzór na okres drgań harmonicznych wahadła:
![]()
Stwierdzamy, że okres małych drgań wahadła nie zależy od wychylenia wahadła z położenia równowagi, zależy natomiast od jego momentu bezwładności I oraz momentu kierującego D.
SPOSÓB WYKONANIA DOŚWIADCZENIA. ETAPY POMIARU.
W ramce przyrządu mocujemy wybraną do badania bryłę. Ustawiamy elektromagnes na zadany kąt α=400 i mocujemy go nakrętką do płyty. Następnie okręcając ramkę powodujemy utrzymanie jej w żądanym położeniu przez elektromagnes. Po zwolnieniu ramka wykonuje drgania skrętne, których liczbę i czas trwania podaje mikrosekundomierz. Skręcona ramka wywiera na oś moment siły M proporcjonalny do α . Równanie ruchu drgającego ramki możemy zapisać w postaci:
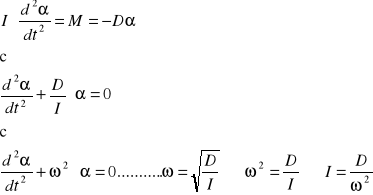
gdzie: D- kątowy moment kierujący
Znając D, ω=2π/T możemy wyznaczyć I.
wyznaczanie momentu kierującego
![]()
Moment kierujący wyznaczamy z zależności:
wyznaczanie momentu siły M.
Prostopadle do ramki działa siła F, która powoduje wychylenie jej o kąt α , równy kątowi zadanemu przez elektromagnes. Jej wartość odczytujemy z wykresu ( w naszym doświadczeniu dla α=400 siła F przyjmuje wartość 0,16 N. Mierząc ramię działania siły ( od środka ramki do elektromagnesu) wyznaczamy moment siły M=F r, a następnie D.
wyznaczanie okresu drgań T
Mierzymy czas t trwania pojedynczego „wahnięcia” dla n drgań i wyznaczamy T korzystając z zależności:
![]()
wyznaczanie momentu bezwładności I
Korzystając ze znanych wartości F, r, T, α wyznaczamy moment bezwładności bryły z zależności:
![]()
gdzie: F- siła powodująca wychylenie z położenia równowagi kąta α
r- ramię siły
T- okres drgań
α- kąt wychylenia pod działaniem siły F
CZĘŚĆ PRAKTYCZNA
Zadaniem naszym podczas przeprowadzanego doświadczenia było odczytywanie czasu t dla przyjętych n=20 „wahnięć” dla zadanego kąta α=400 , stałej siły F (wyznaczonej z wykresu), ramienia r oraz wszystkich różnych osi obrotu danej bryły.
Uzyskane wyniki zestawione zostały w tabelach. Osie obrotu i przyporządkowane im numery prezentują rysunki.
( nr nad tabelą oznacza oś, wg której wyznaczaliśmy moment bezwładności)
BĄK KULISTY
BĄK SYMETRYCZNY BĄK ASYMETRYCZNY
PRZYKŁADOWE OBLICZENIA.
Liczenie I oraz ΔI dla bąka kulistego (dla osi głównej).
Obliczanie ΔI metodą różniczki zupełnej:
Błędy przyrządów:
ΔF=0,0025 N - (z wykresu, jako najmniejsza jednostka (krateczka) )
Δr=0,001 m.
ΔT=0,001 s
Δα=0,017 rad
Zatem:
WNIOSKI.
Podczas przeprowadzania doświadczenia zauważyliśmy, że po włączeniu prądu płynącego przez elektromagnes, na skutek działania momentu sił sprężystych w skręconym drucie (na którym przymocowana była ramka wraz z bryłą) wahadło wykonywało drgania obrotowe. Układ elektroniczny, włączany automatycznie w chwili wyłączenia elektromagnesu mierzył czas trwania pomiaru i liczbę n drgań wykonanych w tym czasie. Okres drgań T=t/n zgodnie ze wzorem
zależał od momentu bezwładności wahadła i momentu kierującego D.
Mierząc okres drgań układu z bryłą odpowiednio zamontowaną w uchwycie wyznaczaliśmy momenty bezwładności I bryły względem żądanej osi (co było celem ćwiczenia). Dla każdej bryły przeprowadzając kilka pomiarów momentu bezwładności względem różnych osi obrotu otrzymaliśmy szereg wartości zestawionych w tabeli.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
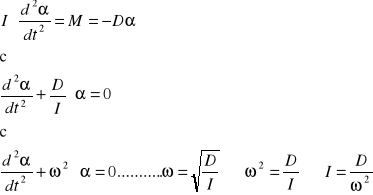
![]()
![]()
![]()
z
x
y
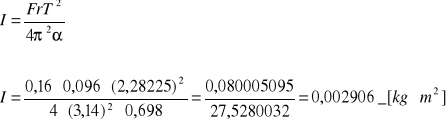

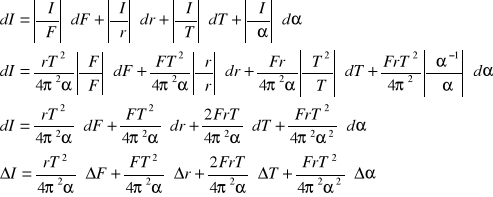
![]()
Wyszukiwarka
Podobne podstrony:
SPRA831, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Laboratorium (metalbob
moja laborka predkosc dzwieku, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik,
moduł szt sprężystych drgań obr, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik
moja laborka predkosc dzwieku nowa, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - cho
PIERŚCIENIE, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Laboratorium (meta
2fiza, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Laboratorium (metalbob),
wilis laborki 1, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Laborki, Moje
wyznaczanie ciepla topnienia lodu, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chom
tabelka do mojej laborki, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Labor
SPRAW 2, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Laboratorium (metalbob
tabela-word, Budownictwo PG, Semestr 2, Fizyka, Laborki Fizyka, Laborki - chomik, Laboratorium (meta
więcej podobnych podstron