Ćwiczenie 42. Wyznaczanie oporu elektrycznego metodą mostka Wheatstone'a

Wstęp:

Celem ćwiczenia jest wyznaczenie oporu R_x, który łączymy szeregowo z oporem wzorcowym R_w. Jedną z prostszych i dokładniejszych metod pomiaru oporu jest porównawcza metoda liniowego mostka Wheatstone'a. W celu wykonania ćwiczenia wolne końce połączonych oporników łączymy z punktami A i C, pomiędzy którymi rozpięty jest drut oporowy wzdłuż podziałki milimetrowej. Punkt B, wspólny dla oporów R_x i R_w, łączymy poprzez miliamperomierz G z suwakiem D, który może swobodnie ślizgać się po drucie. Włączając zasilacz Z prądu stałego, przykładamy napięcie do punktów A i C. Następnie szukamy takiego położenia suwaka D na strunie, aby przez odcinek BD prąd nie płynął.

Wykonanie ćwiczenia:

Pierwsza czynność polega na zestawieniu obwodu elektrycznego zgodnie ze schematem widocznym poniżej, przy czym: R_w - opornik wzorcowy dekadowy, R_x - opornik badany, Z - źródło prądu stałego, G - galwanometr (miliamperomierz), W - wyłącznik z oporem zabezpieczającym.

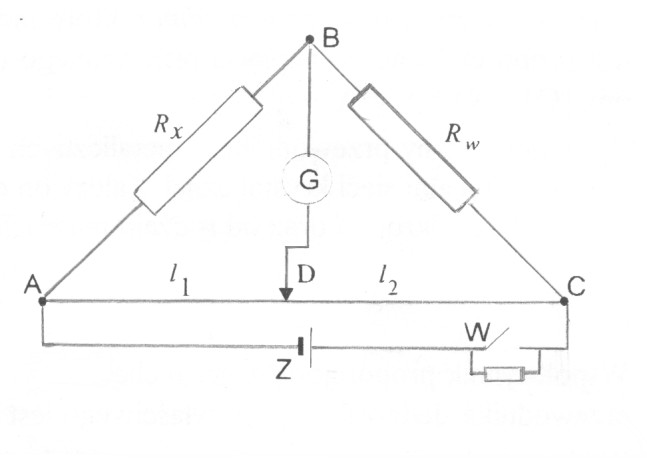
Następnie przy otwartym wyłączniku W ustawiamy opornicę dekadową na wartość 10Ω i włączamy zasilacz Z. Dobieramy położenie suwaka D na strunie tak, aby galwanometr wskazywał wartość zero. Po zamknięciu klucza W położenie to ustalamy bardziej precyzyjnie i odczytujemy długości odcinków l₁ i l₂. Po odczytaniu tych wartości obliczamy wartość szukanego oporu - jest to wartość orientacyjna, obarczona dość dużym błędem pomiarowym. Oznaczamy wyznaczoną wartość R_x jako R₀.

Postępując jak wyżej wykonujemy trzy pomiary oporu R_x: ustawiamy na opornicy dekadowej kolejno trzy różne, ale bliskie R₀ wartości oporu wzorcowego. Otrzymujemy w ten sposób trzy wartości R₁, R₂, R₃. Jako wartość oporu R_a przyjmujemy średnią arytmetyczną równą (R₁+R₂+R₃)/3. Identycznie wyznaczamy opór następnego opornika - R_b.

W następnej części ćwiczenia łączymy badane oporniki szeregowo i dokonujemy pomiaru oporu wypadkowego za pomocą mostka Wheatstone'a. Tak samo postępujemy w przypadku połączenia równoległego.

Rachunek błędów:

Błąd względny pomiaru, ∆R_x/R_x, obliczamy ze wzoru:

Obliczam błąd względny pomiaru
dla przewodnika
wykorzystując w tym celu pomiar nr 0, w którym wartości
i
odbiegają najbardziej od zalecanego ustawienia suwaka tzn. w połowie długości struny.

Następnie obliczam błąd względny dla pomiaru nr 3, w którym wartości
i
są najbliższe zalecanego ustawienia suwaka na strunie.

Na podstawie otrzymanych wyników mogę przypuszczać, że pomiary nr 1 i 2 zawierają się między
,a
.

Skoro wyniki powyższych obliczeń spełniają założenia ćwiczenia - (jeśli wartości
i
są sobie równe -to błąd pomiaru jest najmniejszy). W związku z tym wystarczy obliczyć błąd względny pomiaru nr 0 dla przewodnika
, gdyż odbiega on najbardziej od zalecanego ustawienia suwaka na strunie. Błędy pozostałych pomiarów będą mniejsze niż ta wartość.

Tak, więc błąd pomiarów nr 1,2 i 3 jest mniejszy niż
.

Wnioski:

Najprawdopodobniej błąd, (choć nie duży) wynikać może z trudności z bardzo dokładnym odczytem wartości długości
i
, jak również najmniejszej wartości przesunięcia suwaka na strunie, dla której występuje zauważalne przemieszczenie wskazówki galwanometru. Kolejnym powodem może być stan techniczny urządzeń użytych do pomiarów.

---