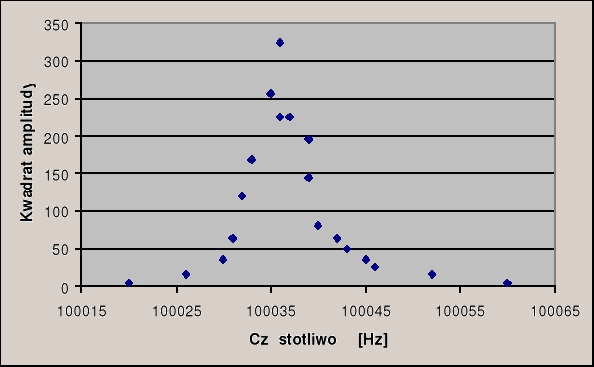
Politechnika Śląska

Wydział AEiI

Laboratorium z fizyki

Rezonator kwarcowy

Grupa 6., sekcja 12.

Michał Nycz

Piotr Jelonek

Wstęp teoretyczny.

Oscylator harmoniczny jest to punkt materialny o masie m, wykonujący ruch pod wpływem siły sprężystej:

F = -kx

gdzie:

x - wychylenie od położenia równowagi ;

k - stała sprężystości ( współczynnik proporcjonalności między siłą a wychyleniem ).

W mechanice klasycznej równanie ruchu oscylatora harmonicznego

ma rozwiązanie x = A cos(t) , które przedstawia drgania oscylatora harmonicznego wokół położenia równowagi z częstością kołową :

i amplitudą A. Energia tych drgań jest równa energii potencjalnej tej cząstki w położeniu największego wychylenia:

Rezonatorem nazywamy oscylator o dużej dobroci. Przyjmuje on energię tylko w zjawisku rezonansu. Taki oscylator pobudzony do drgań wykonuje przed zatrzymaniem wiele wahnięć.

Dobroć ( współczynnik dobroci ) jest to stosunek energii zmagazynowanej w układzie drgającym do energii traconej w jednym okresie drgań. Jest to parametr charakteryzujący zdolność oscylatora do wykonywania drgań niewymuszonych. Wielkość ta jest mniej więcej równa ilości oscylacji, jakie rezonator wykona po odłączeniu generatora.

Opis stanowiska pomiarowego.

Stanowisko pomiarowe przystosowane jest do wyznaczania dobroci rezonatora kwarcowego. Na stanowisku znajduj --> [Author:AM] ą się:

1. rezonator kwarcowy o nominalnej wartości 100 kHz;

2. generator LC o przebiegu sinusoidalnym;

3. oscyloskop dwukanałowy;

4. częstościomierz o dokładności 1 Hz.

Obliczenia.

W ramach doświadczenia zostały dokonane pomiary amplitudy drgań rezonatora w zależności od ich częstotliwości. Wyniki tych pomiarów zebrane zostały w poniższej tabeli:

Częstotliwość [Hz]	Amplituda
100060	2
100052	4
100046	5
100045	6
100043	7
100042	8
100040	9
100039	12
100039	14
100037	15
100036	15
100036	18
100035	16
100033	13
100032	11
100031	8
100030	6
100026	4
100020	2

W oparciu o zebrane dane utworzony został wykres zależności kwadratu amplitudy od częstotliwości:

Z wykresu należało odczytać szerokość połówkową krzywej rezonansowej f

( szerokość maksimum w połowie jego wysokości ), oraz częstotliwość rezonansową f₀.

Aby odczyt wyżej wymienionych wartości był dokładniejszy, utworzony został wykres pomocniczy, obejmujący górną połowę poprzedniego:

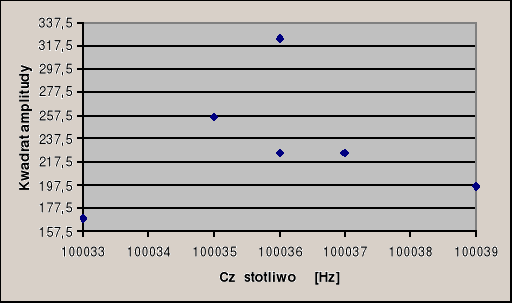
Kwadrat amplitudy drgań przyjmuje połowę wartości maksymalnej dla częstotliwości równych ( przy czym błąd odczytu wartości z wykresu wynosi 0,1 Hz):

f₁ = 100033 ± 1 Hz

f₂ =100039 ± 1 Hz

wobec tego szerokość połówkowa krzywej rezonansowej wynosi:

f = f₂ - f₁

f = 6 ± 1 Hz

Kwadrat amplitudy przyjmuje maksymalną wartość ( 324 ) dla częstotliwości :

f₀ = 100036 ± 1 Hz

Dobroć układu drgającego obliczamy ze wzoru:

i wynosi ona:

Q = ( 16 ± 2 ) * 10³

Wnioski.

Otrzymany przez nas wykres odbiega od oczekiwanego , ponieważ skoki częstotliwości przekraczały 10 Hz w krótkich przedzialach czasu. Uniemożliwiało to dokładne wyznaczenie amplitudy dla konkretnej częstotliwości. Bład powiekszyła także przyjęta metoda obliczeń.

---