Pobierz dokument cw.nr.5.05.doc Rozmiar 29 KB

I ED	KOWAL WALDEMAR	grupa l3
98-III-02	Wyznaczanie wartości =Cp/Cv dla powietrza metodą Clementa i Desomesa	Ćwiczenie Nr 5

1. Cel ćwiczenia :

- wyznaczenie wartości  = Cp / Cv dla powietrza metodą Clementa i Desormesa

2. Przyrządy pomiarowe :

- butla szklana o pojemności około 10 litrów

- pompka tłocząca

- manometr

3. Program ćwiczenia :

- zamknąć kurek K1 i zagęszczać w butli powietrze za pomocą pompki do momentu ,

gdy różnica poziomów cieczy manometrycznej wyniesie kilka podziałek

- odczekać kilka minut , by różnica poziomów w manometrze ustaliła się , odczytać

ją i oznaczyć h1

- otworzyć kurek K1 ( około 0.2 - 0.5 sekundy ) aby ciśnienie w butli wyrównało się

z ciśnieniem atmosferycznym

- odczekać kilka minut , aż wskazania manometru ustalą się . Zapisać nadwyżkę

ciśnienia h2 . Obliczyć wartość 

- w celu osiągnięcia lepszej dokładności należy pomiary wykonać kilkakrotnie , za

każdym razem ponawiając sprężenie gazu .

- przeprowadzić dyskusję błędów metodą różniczkową

4. Tabelka z wynikami pomiarów

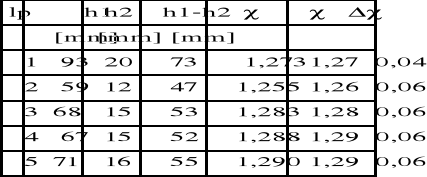
5. Wstępna dyskusja błędów

Podczas wykonywania pomiarów mogły wystąpić błędy związane z niedokładnym

odczytem wartości ciśnień h1 oraz h2 mierzonych w milimetrach słupa cieczy

manometrycznej . Wartości powyższe odczytywane były z uwagi na dokładność

podziałki , z dokładnością 1 mm . Błąd odczytu powiększało również zjawisko

menisku wklęsłego w rurce szklanej manometru . Zkładam , że błąd spowodowany

tym zjawiskiem rzutował na wynik pomiaru błędem odczytu rzędu 1 mm .

Biorąc pod uwagę powyższe błędy oraz błąd niedokładnego odczytu przez

przeprowadzającego pomiary , zakładam że całkowity błąd wnoszony podczas

pomiaru wynosi odpowiednio : h1= 2 mm oraz h2= 2mm .

6. Różniczkowa dyskusja błędów

Wartość wykładnika adiabatycznego obliczamy ze wzoru :   h1 / (h1-h2)

Wartość  wyznaczyć można korzystając z metody różniczki zupełnej .

  δδh1| h1 + | δδh2 | h2

Po obliczeniu pochodnych wzór będzie miał postać :

  (-h2) / (h1-h2)2 |  h1 + | h1 / (h1-h2)2 | h2

Po uproszczeniu wzór przyjmie postać :

( h2 h1 + h1 h2) / ( h1 - h2)2

Błąd względny procentowy możemy obliczyć w następujący sposób (dzielę oobie

strony przez  )

[( h2 h1 + h1 h2) / ( h1 - h2)2] [( h1- h2)/h1 ]

Po wykonaniu dzielenia otrzymuję :

[ h2 h1 / h1(h1-h2)] + h2 / ( h1 - h2)]

Błąd względny procentowy będzie równy : ( )100%

7. Dyskusja błędów

Powietrze jest głównie gazem dwuatomowym stąd też wynika , że poprawna wartość

wykładnika adiabatycznego jest 1,4 . Wyniki pomiarów wykazały odchyłkę od tej wartości . Na nieprawidłową wartość wyniku wpływ mogły wywrzeć następujące czynniki :

- nieszczelność aparatury pomiarowej mogła powodować powolne ulatnianie się sprężonego gazu z butli ( mogło dojść do wymiany ciepła z otoczeniem ) , tym samym

ciśnienie gazu w butli (h2) spadało , powodując błędne ustalenie się słupa cieczy w manometrze ( odczytywano zbyt niską wartość ciśnienia h2 )

- zbyt krótki czas na ustalenie się poziomu cieczy manometrycznej po sprężeniu i po rozprężeniu gazu mógł być powodem błędnych wskazań . Według instrukcji czasy te

powinny być rzędu kilku - kilkunstu minut , podczas pomiaru na ustalenie ciśnienia czekano około 3 - 4 minut . Jednak zbyt długi czas mógłby powodować zwiększony wpływ nieszczelności układu pomiarowego

- zalecany czas otwarcia kurka K1 rzędu 0,2 - 0,5 sekundy był zbyt krótki na wyrównanie się ciśnienia w butli z ciśnieniem atmosferycznym , konieczne było dłuższe

otwarcie . Czynność ta ma największe znaczenie dla uzyskania dokładnego pomiaru .

Zbyt długie otwarcie zaworu K1 mogło sprawiać , że gaz podczas rozprężania pobierał ciepło z otoczenia więc jego rozprężanie nie było w pełni adiabatyczne .

- osłona adiabatyczna butli mogła okazać się niedoskonałym izolatorem cieplnym co mogło prowadzić do wymiany ciepła z otoczeniem .

---

Pobierz dokument cw.nr.5.05.doc Rozmiar 29 KB