ZARZĄDZANIE GOTÓWKĄ

MODEL BAUMOLA

Przykład

Przedsiębiorstwo potrzebuje w ciągu określonego czasu T gotówki w ilości R.

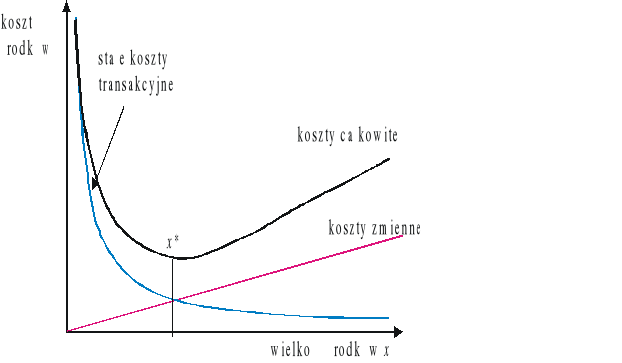
Zapotrzebowanie na gotówkę rozkłada się w sposób równomierny, rys.

Należy ustalić, jakimi transzami pobierać gotówkę z banku, aby koszty pobierania gotówki i koszty utrzymania gotówki w kasie (magazynowania) były możliwie najmniejsze.

Załóżmy, że

k₁ - jednostkowy koszt utrzymania gotówki w kasie (magazynowania), koszt magazynowania jednej złotówki na jedną jednostkę czasu.

K₂ - koszty pobrania jednej transzy

K₂ = C+k₂ -

C - koszty niezależne od wielkości transzy (zmienne koszty związane z angażowaniem złotówek)

k₂ - koszty zależne od ilości transz - koszty uruchomienia transzy

UWAGA

Wielkość transzy = R, to wysokie koszty magazynowania i niewielkie uruchomienia transz,

Wielkość transzy = 1 zł, to niewielkie koszty magazynowania gotówki, ale wysokie koszty uruchamiania transzy.

W zadaniu, należy znaleźć taką wielkość transzy X, która będzie minimalizowała koszty łączne: przechowywania gotówki (magazynowania) i uruchomiania transz.

Niech, np.

gdzie L - pewna dodatnia liczba, np. L=4, wówczas

Liczba okresów czasu L = R/X, a ich długość oznaczmy t. Stan gotówki w kasie na początku każdego okresu czasu wynosi X, a na końcu 0.

Z założenia o równomierności zapotrzebowania na gotówkę wynika, że

Średni stan kasy wynosi

Zatem, koszt przetrzymywania gotówki w kasie K_m w okresie T wynosi

Wielkość t zależy od wybranej wielkości transzy X,

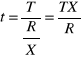
Zatem

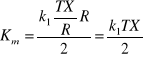
Koszty uruchomienia transz K_p, wynoszą

Łączne koszty

,

które należy minimalizować. Jest to więc funkcja kryterium.

Należy znaleźć takie X = X₀ > 0, które minimalizuje funkcję kosztów K.

Zatem, obliczamy pierwszą pochodną K po X

i

Rozwiązujemy to równanie i otrzymujemy

,

a stąd

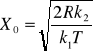
Druga pochodna

dla X = X₀,

bo jeśli R, k₁, k₂, T > 0, to

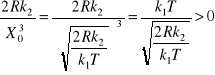
PRZYKŁAD

Przedsiębiorstwo potrzebuje rocznie 120 000zł gotówki.

Koszt utrzymania 1zł w kasie wynosi 10 gr.

Jednostkowy koszt przeprowadzenia transakcji wynosi 500zł.

Obliczyć optymalne transze gotówki, jeśli jednostką czasu będzie 1 miesiąc.

Rozwiązanie:

k₁ = 0.1zł/1zł

k₂ = 500zł

T = 12

=

= 10 000zł

co miesiąc.

PRZYKŁAD

Zapotrzebowanie R = 40 0000 w okresie czasu T = 12 miesięcy.

Niech jednostkowy koszt magazynowania k₁ - 2zł, a koszt uruchomienia produkcji jednej partii k₂ = 1200zł. Wówczas

a produkcję należy uruchamiać co

miesiąca,

czyli co 18 dni.

1

8

Stan kasy

R

T

Stan kasy

T

R/44

T/4

Koszt uruchomiania transz

Koszt utrzymania gotówki w kasie

---