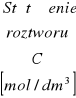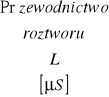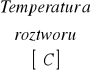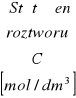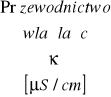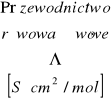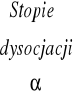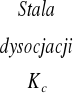POLITECHNIKA SZCZECIŃSKA

ZAKŁAD CHEMII FIZYCZNEJ

Laboratorium studenckie

Sprawozdanie z wykonania ćwiczenia nr 17:

„Wyznaczanie zależności przewodnictwa elektrolitów od stężenia, oraz wartości stałej dysocjacji kwasu octowego metodą konduktometryczną.”

APARATURA: - konduktometr

• termometr

• pipeta na 20 cm³

• zlewki na 100 i 250 ml

• naczynko pomiarowe

ODCZYNNIKI: - 0.0625n roztwór CH₃COOH

• 0.005n roztwór KCl

• 0,1n NaCl

• 0,1n HCl

• 0,1n CH₃COONa

• woda redestylowana

WYKONANIE:

Stopień dysocjacji słabych elektrolitów, zależy w wyraźny sposób od stężenia. Charakter tej zależności można określić na drodze rozważań termodynamicznych. Pomiędzy cząsteczkami niezdysocjowanymi powstałymi w wyniku ich dysocjacji jonami, ustala się bowiem stan równowagi termodynamicznej z charakterystyczną dla danego elektrolitu stałą dysocjacji, która nie zależy od stężenia, a jest tylko funkcją temperatury i ciśnienia.

Dla słabego elektrolitu, np. kwasu
, który dysocjuje na jony
i
termodynamiczną stałą dysocjacji
opisuje zależność:

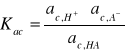
gdzie przez
,
i
oznaczone zostały aktywności stężeniowe odpowiednich jonów
,
i cząsteczek niezdysocjowanych
. Aktywność i-tego składnika roztworu
można wyrazić w postaci:

gdzie
oznacza stężenie tego składnika (mol/dm³),
- stężenie standardowe równe 1 mol/dm³, a
to współczynnik aktywności, który jest miarą oddziaływań i-tego składnika z pozostałymi składnikami roztworu. Jeśli całkowite stężenie elektrolitu oznaczyć jako
, a jego stopień dysocjacji jako
, to zgodnie z jego definicją stężenia jonów i cząsteczek niezdysocjowanych można wyrazić następująco:

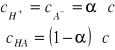
Z przedstawionych równań, w wyniku kolejnych podstawień, otrzymuje się równanie:

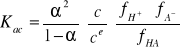
określa ono charakter zależności między stopniem dysocjacji i stężeniem roztworu.

Duże znaczenie praktyczne ma prawo rozcieńczeń Ostwalda:

gdzie
jest tzw. klasyczną stałą dysocjacji. Stałą tą, można bardzo prosto wyznaczyć eksperymentalnie. Wystarczy w tym celu określić stopień dysocjacji danego elektrolitu. W przypadkach dostatecznie rozcieńczonych roztworów można posłużyć się zależnością:

gdzie
to przewodnictwo równoważnikowe danego roztworu zdefiniowane równaniem:

w którym
oznacza przewodnictwo właściwe tego roztworu,
jego stężenie, a
jest przewodnictwem równoważnikowym w granicznie rozcieńczonym roztworze.

W przeciwieństwie do termodynamicznej stałej dysocjacji
, która zależy tylko od temperatury, stała klasyczna
zależy również od stężenia roztworu. Ponieważ w miarę rozcieńczania roztworu wzajemne oddziaływania między składnikami elektrolitu maleją i współczynniki aktywności przybierają wartości coraz bardziej zbliżone do jedności, więc nie trudno wykazać, że:

Relację tą można wykorzystać do określania termodynamicznej stałej dysocjacji
dla różnych stężeń jego roztworów.

1. Zestawienie wyników.

1.	0,0625	450	16,5
2.	0,0313	320
3.	0,0156	125
4.	0,0078	88
5.	0,0039	110
6.	0,0020	73
7.	0,001	50
1.	0,005	0,77 [mS]	17,8
1.	0,1	17500	16
2.	0,05	5600
3.	0,025	3050
4.	0,0125	1050
5.	0,0063	790
6.	0,0032	390
7.	0,0016	112
1.	0,1	37 [mS]	17
2.	0,05	20 [mS]
3.	0,025	11 [mS]
4.	0,0125	5,5 [mS]
5.	0,0063	2,83 [mS]
6.	0,0032	0,36 [mS]
7.	0,0016	0,65 [mS]
1.	0,1	6,7 [mS]	16,5
2.	0,05	3,8 [mS]
3.	0,025	1,9 [mS]
4.	0,0125	1,05 [mS]
5.	0,0063	0,5 [mS]
6.	0,0032	140
7.	0,0016	130

2. Obliczenia stałej C ze wzoru:

3. Obliczenia
,
,
i
dla kwasu octowego.

1.	0,0625	361,485	5,78376	0,016	0,016 ⋅ 10^-3
2.	0,0313	257,056	8,21265	0,023	0,0169 ⋅ 10^-3
3.	0,0156	100,412	6,43666	0,018	5,14 ⋅ 10^-6
4.	0,0078	70,690	9,06282	0,026	5,41 ⋅ 10^-6
5.	0,0039	88,363	22,6571	0,065	0,017 ⋅ 10^-3
6.	0,0020	58,640	29,32	0,085	0,015 ⋅ 10^-3
7.	0,001	40,165	40,165	0,116	0,0152 ⋅ 10^-3

Obliczenia powyższe przeprowadzone zostały przy pomocy równań:

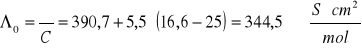
Obliczenie
potrzebne do sporządzenia wykresu:

1. 0,031 5. 0,015

2. 0,026 6. 0,013

3. 0,016 7. 0,010

4. 0,014

Wartość
odczytana z wykonanego wykresu wynosi 14 ⋅ 10^-6, natomiast wartość tej stałej odczytana z poradnika fizyko-chemicznego wynosi 1,753 ⋅ 10^-5.

Obliczenia błędu pomiaru:

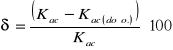
6

---