8. Funkcje wymierne

Funkcję będącą ilorazem dwóch wielomianów
określoną na zbiorze

nazywamy funkcją wymierną.

Ważnym przykładem funkcji wymiernej jest funkcja homograficzna, tzn. funkcja postaci

gdzie
i
Jeżeli
, to funkcja f określona powyższym wzorem jest funkcją liniową, a gdy
, f jest funkcją stałą (pomijamy tu „patologiczny” przypadek, gdy
Obie te funkcje nie są funkcjami homograficznymi. Szczególnym przy­pad­kiem funkcji homograficznej jest proporcjonalność odwrotna
gdzie

Przykład. Podamy wykresy niektórych funkcji wymiernych.

Widzimy, że wykresy funkcji wymiernych mogą przybierać różne kształty. Wykresem funkcji homograficznej jest jednak zawsze hiperbola. Otrzymujemy ją z wykresu funkcji
stosując odpowiednie przesunięcia.

Przykład. Naszkicujemy wykres funkcji

Rozwiązanie. Zauważmy, że

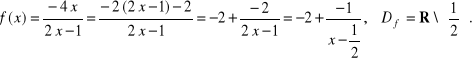
Zatem, aby otrzymać wykres badanej funkcji, należy przesunąć wykres funkcji
o wektor
lub, co łatwiejsze, układ współrzędnych o wektor

W ogólnym przypadku funkcji homograficznej mamy

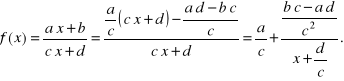
Dlatego jej wykres otrzymujemy przesuwając wykres funkcji
gdzie
o wektor
Stąd wynika wniosek:

Wykresem funkcji homograficznej
gdzie
jest hiperbola. Asymptotami wykresu tej funkcji są proste o równaniach
i
.

Równaniami (nierównościami) wymiernymi nazywamy równania (nierówności) postaci:

gdzie
są wielomianami. Są to więc równania lub nierówności, w których występują ułamki algebraiczne.

Aby rozwiązać równanie sprowadzalne do równania wymiernego najczęściej należy:

1. Ustalić dziedzinę równania.

2. Pomnożyć obie strony równania przez wspólny mianownik występujących tam ułamków alge­braicznych, w konsekwencji czego otrzymujemy równanie wielomianowe.

3. Rozwiązać otrzymane równanie wielomianowe.

4. Sprawdzić, które rozwiązania równania wielomianowego należą do dziedziny równania wy­miernego.

Oczywiście w szczególnych przypadkach może istnieć inna, szybsza me­to­da rozwiązania danego równania.

Przykład. Rozwiążemy równanie

Rozwiązanie. Rozpoczynamy od zastrzeżeń:
Mamy dalej

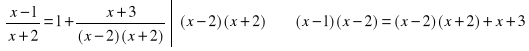
Ponieważ liczba
należy do dziedziny równania, więc jest ona jego rozwiązaniem.

Aby rozwiązać nierówność sprowadzalną do nierówności wymiernej należy:

1. Ustalić dziedzinę nierówności.

2. Uporządkować nierówność, tzn. przenieść wszystkie wyrażenia na jedną stronę, doprowadzić do wspólnego mianownika i wykonać redukcję wyrazów podobnych po to, aby doprowadzić ją do jednej z postaci:
lub

3. Pomnożyć obie strony nierówności przez kwadrat mianownika
co sprowadzi ją do nierówności wielomianowej.

4. Rozwiązać otrzymaną nierówność.

5. Porównać rozwiązania nierówności wielomianowej z dziedziną nierówności wymiernej
i ewentualnie usunąć ze zbioru rozwiązań punkty spoza dziedziny nierówności.

Powyższą „instrukcję” można modyfikować wykorzystując dodatkowe informacje dotyczące własności poszczególnych mianowników. Można również zastąpić kroki 2 i 3 pomnożeniem obu stron nierówności przez kwadrat wspólnego mianownika poszczególnych ułamków algebraicznych występujących w tej nierówności, a w konkretnych przypadkach nawet zastosować zupełnie inne postępowanie.

Przykład. Rozwiążemy nierówność

Rozwiązanie. Widać, ze musi być spełnione zastrzeżenie:
Mamy

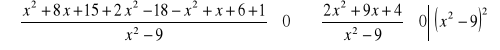
Rozkładamy na czynniki otrzymane trójmiany kwadratowe:

Szkicujemy

uproszczony wykres wielomianu
i odczytujemy z nie­go rozwiązanie nierówności wielomianowej:

Stąd

Po uwzględnieniu zastrzeżeń ostatecznie stwierdzamy, że nierówność
spełniają punkty

Rozdział 8. Funkcje wymierne 68

66

x

y

4

2

x

y

1

-1

1

x

x

y

−4

−3

3

x

y

x

---