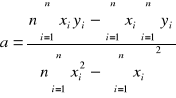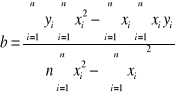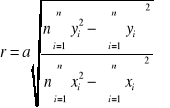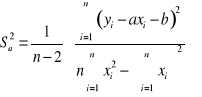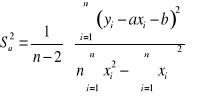Każde działanie na ciało jakąś siłą powoduje zachodzenie zmian w jego strukturze co obserwujemy w postaci odkształcenia. Można je podzielić na: postaci (w wyniku którego następuje zmiana pierwotnego kształtu ciała), objętości (w wyniku ciśnienia ściskającego ciało ze wszystkich stron), bezwzględne (będące różnicą pomiędzy długością ciała odkształconego poprzez działająca siłę, a jego pierwotną długością), względne (które jest stosunkiem odkształcenia bezwzględnego do pierwotnej długości tego ciała). A także na sprężyste, czyli takie gdzie po ustaniu siły odkształcającej powraca ono do swojej pierwotnej postaci oraz na trwałe, gdy ciało trwale zmienia swój kształt w wyniku przyłożonej siły odkształcającej. Dodatkowo, odkształcenia postaci można podzielić na: rozciąganie, ściskanie, zginanie, skręcanie czy ścinanie. To co dzieje się w ciele odkształcanym ilustruje wykres naprężenia od odkształcenia względnego. Pierwszy fragment tego wykresu to zakres proporcjonalności w którym spełnione jest prawo Hooke'a według którego odkształcenie względne ciała jest proporcjonalne do przyłożonej siły i odwrotnie proporcjonalne do pola jego przekroju. Stałą proporcjonalności jest tutaj moduł Younga (E), będący stałą charakterystyczną dla danego materiału. Jeżeli zamiast stosunku siły do powierzchni wstawimy naprężenie, a odkształcenie względne wyrazimy poprzez wielkość ε, to prawo to przyjmie postać: σ= ε*E Oprócz przytoczonego tu modułu sprężystości, który jest współczynnikiem proporcjonalności przy rozciąganiu lub ściskaniu (gdy na ciało działają siły normalne - prostopadłe do powierzchni) występuje także moduł sztywności mający swe zastosowanie w zjawisku ścinania (gdy siły działające na ciało są równoległe do powierzchni) oraz moduł sprężystości objętościowej (gdy ciśnienie ściska całą objętość materiału). Jeżeli przekroczymy granicę proporcjonalności to przebieg odkształceń odbiegać będzie od powyżej zależności. Skończy się on po osiągnięciu naprężenia o nazwie granicy elastyczności. Następnie ciało ulega odkształceniom plastycznym w których następuje przyrost długości bez wyraźnego wzrostu naprężeń. Po przekroczeniu granicy plastyczności, kolejne naprężenia doprowadzą do granicy wytrzymałości doraźnej, czyli naprężenia powyżej którego nastąpi zerwanie próbki
Celem ćwiczenia było zbadanie i porównanie właściwości różnych metali poprzez porównanie modułów Younga. W celu obliczenia pola przekroju poprzecznego ze wzoru 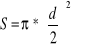
, śrubą mikrometryczną zmierzono średnicę „d” obu drutów. Następnie, ze wzoru 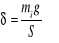
obliczono naprężenia poprzeczne działające na druty dla odpowiednich mas mi. Obciążono druty stalowe dziesięcioma ciężarkami o masie m1= 5,755kg i odczytano wskazania wydłużeń bezwzględnych (Δl) obu drutów. Analogicznie postąpiono zdejmując kolejne odważniki. Ze wzoru ε = Δl/l obliczono
wydłużenia względne obu drutów. Wyniki zebrano w tabelach:
Dla druta stalowego o długości początkowej l0=1,58m i średnicy d=0,70mm (S=0,385*10-6 m2)
|
|
Naprężenie poprzeczne
σ [MPa]
|
Wskazania mikromierza
xi [10-3 m]
|
Wydłużenie względne ε [10-3]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dla druta stalowego o długości początkowej l0=1,48m i średnicy d=0,70mm (S=0,385*10-6 m2)
|
|
Naprężenie poprzeczne
σ [MPa]
|
Wskazania mikromierza
xi [10-3 m]
|
Wydłużenie względne ε [10-3]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Następnie w celu skorzystania z metody najmniejszych kwadratów sporządzono tabele wg wzorów z instrukcji F17.
Dla druta stalowego o długości początkowej l0=1,58m
Dla druta stalowego o długości początkowej l0=1,48m
Korzystając z załączonych tam wzorów, obliczono moduły Younga będące wartościami a:
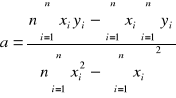
Dla drutu o długości 1,58m a =1,808*1011 Pa co daje wartość E1= 180,8 GPa
Dla drutu o długości 1,48m a =1,024*1011 Pa co daje wartość E1= 102,4 GPa
Następnie wartość b (będącą miejscem przecięcia wykresu funkcji naprężenia od wydłużenia względnego z osią OY), ze wzoru:
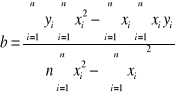
b1 = - 2,4*107 [Pa] b2 = 6,3*106 [Pa]
Oraz współczynnik korelacji „r” będący miarą rozrzutu σ i ε
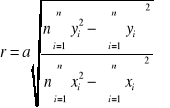
r1 = 0,999 r2 = 0,988
Aby poznać błąd pomiaru modułu Younga, obliczono odchylenie standardowe, korzystając ze wzoru:
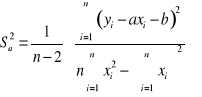
Sa1 = 1026833192 Pa
1 GPa
Sa2 = 1789399185 Pa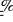
2 GPa
A więc moduły Younga wyznaczone dla drutów stalowych wynoszą odpowiednio:
Dla druta stalowego o długości 1,58m
E1 =( 181
1) GPa
Dla druta stalowego o długości 1,48m
E2 =( 102
2) GPa
Dla porównania, wartości tablicowe modułów Younga dla stali węglowej wynoszą od 190 do 210 GPa.
Wnioski:
Powyższe badanie umożliwiło nam zapoznanie się z metodą wyznaczania modułów Younga oraz przypomnienie prawa Hooke'a.
Na niepewności pomiaru miały wpływ takie czynniki jak:
- niedokładność urządzeń pomiarowych - niepewność związana z odczytem wskazania wydłużenia względnego mikromierza oraz pomiaru średnicy drutów
- klasa urządzeń pomiarowych - mikromierz, śruba mikrometryczna, szalka z odważnikami
- jakości oraz długości materiałów użytych w doświadczeniu - druty „zmęczone” wielokrotnym rozciąganiem mogą wykazywać inne właściwości, w tym wartości cech materiałowych jak np. moduł Younga
- błędy wynikające z przyjętej dokładności prowadzenia obliczeń
- wpływ czynnika ludzkiego - po każdorazowym zawieszeniu szalki z obciążeniem należało ustawić ją w położeniu równowagi (tak, aby się nie odchylała) przed odczytaniem wartości wydłużenia względnego
Dodatkowo na niepewności pomiaru wpływ mogły mieć nierówności występujące na powierzchni druta - zwłaszcza podczas pomiaru jego średnicy, nierówności mogły spowodować błędny odczyt, co
diametralnie mogło zmienić wyniki.
Na podstawie porównania wyników obliczonych wielkości fizycznych z wartościami tablicowymi, można stwierdzić, że wartość ta jest zbliżona w przypadku drutu dłuższego. Natomiast druga próbka materiału wykazała wartości o połowę mniejsze, zarówno w stosunku do pierwszej jak i do wartości tablicowych. Może to wskazywać na powstanie odkształcenia trwałego wywołanego wielokrotnym jej rozciąganiem jeżeli była ona wykonana z tego samego materiału i tą samą metodą co pierwsza.
Obliczone współczynniki korelacji r, których wartości były bliskie jedności oraz sporządzone wykresy naprężenia w funkcji wydłużenia względnego pozwalają stwierdzić, że wyznaczone zależności są liniowe, co pokrywa się z prawem Hooke'a. Eliminuje to także błąd gruby z rozważań nad odbiegającym od tablicowego wyniku dla próbki drugiej.
Powyższe rozważania pozwalają skonstatować, że nawet dwa takie same materiały jak stal o identycznej średnicy, poddawane identycznym naprężeniom mogą wykazywać odmienne właściwości wyrażone wartościami cech materiałowych (w tym przypadku modułów Younga) w zależności od stopnia ich eksploatacji.
Wiktor Adamski i Ilona Łakomiec, Nanotechnologia, semestr II, grupa 1., gr. laboratoryjna 14.
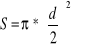
![]()