Podstawowe wzory na całki
Funkcją pierwotną funkcji ![]()
w przedziale ![]()
nazywamy każdą funkcję ![]()
taką, że ![]()
dla każdego ![]()
z przedziału ![]()
.
Dwie funkcje mające w danym przedziale tę samą skończoną pochodną mogą się różnić co najwyżej o stałą.
Całką nieoznaczoną funkcji ![]()
, oznaczaną symbolem
![]()
nazywamy wyrażenie ![]()
, gdzie ![]()
jest funkcją pierwotną funkcji ![]()
, a ![]()
jest dowolną stałą.
Mamy więc
![]()
, gdzie ![]()
Podstawowe wzory rachunku całkowego
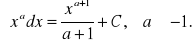
Kilka szczególnych przypadków tego wzoru to:dla
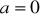
: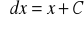
;dla
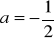
: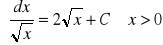
;dla
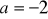
: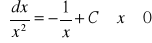
.
![]()
.
![]()
![]()
.
![]()
![]()
![]()
![]()
![]()
![]()
Własności całek nieoznaczonych:
Całka sumy równa się sumie całek, (addytywność całki względem sumy podcałkowej) tzn.
![]()
Stały czynnik można wynieść przed znak całki, tzn.:
![]()
(Całkowanie przez części ) Jeżeli
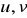
są funkcjami zmiennej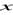
mającymi ciągłą pochodną, to
![]()
(Całkowanie przez podstawienie) Jeżeli dla
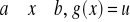
jest funkcją mającą ciągłą pochodną oraz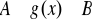
, a funkcja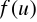
jest ciągła w przedziale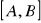
, to
![]()
przy czym po scałkowaniu prawej strony należy w otrzymanym wyniku podstawić ![]()
.
Wyszukiwarka