Tw. Jeżeli X jest zmienną losową typu skokowego , Y=g(X) oraz ![]()
( jest zbieżny) to ![]()
WYKŁAD 5 13.11.2003
(by elle)
Tw. Jeżeli X jest zmienną losową typu skokowego , Y=g(X) oraz ![]()
( jest zbieżny) to ![]()
Tw. Jeżeli X jest zmienną losową typu ciągłego , Y = g(x) oraz ![]()
(jest zbieżna) to ![]()
I. Wybrane rozkłady ciągłe:
rozkład normalny
gęstość : 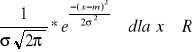
σ - parametr skali σ>0
m - parametr przesunięcia m![]()
R
N(m,σ) - rozkład normalny z parametrami m i σ
m1=E(X)=m wartość oczekiwana
D2(X)=μ2=σ2 wariancja , 2-gi moment zwykły
X0,5=Me=m mediana dla rozkładu normalnego
Każdy moment centralny rzędu nieparzystego jest równy zero , czyli ![]()
Momenty centralne rzędu parzystego wyrażają się wzorem ![]()
, (2r-1)!! - iloczyn kolejnych liczb nieparzystych(tylko) , dowód : μ2=1!!*σ2*1 = σ2
Odchylenie standardowe : ![]()
![]()
- współczynnik asymetrii, rozkład normalny jest rozkładem symetrycznym względem prostej x=m ![]()
![]()
, ![]()
, ![]()
,![]()
, ![]()
, ![]()
Reguła trzy-sigmowa
Prawie wszystkie wartości zmiennej X zawarte są w przedziale (m-3σ,m+3σ) Standaryzacja rozkładu normalnego X~N(m,σ) x ma rozkład normalny z parametrami m,σ to ![]()
ma rozkład normalny z parametrami N(0,1) . Rozkład N(0,1) nazywa się standaryzowanym rozkładem normalnym.
Funkcja gęstości rozkładu N(0,1) → 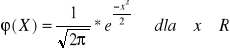
Dystrybuanta N(0,1) 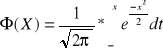
zmienna T nazywa się standaryzowaną zmienną losową
rozkład gamma Eulera
Z rozkładem gamma związana jest funkcja gamma określona wzorem : 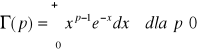
![]()
jest funkcją ciągłą ![]()
![]()
gęstość dla rozkładu gamma Eulera 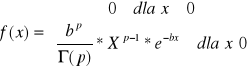
gdzie b>0 i p>0
szczególnym przypadkiem rozkładu gamma Eulera (dla p=1, ![]()
, λ>0)
rozkład wykładniczy 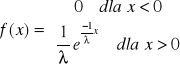
![]()
- parametr, λ>0
Zastosowanie rozkładu wykładniczego:
przyjmuje się, że czas bezawaryjnej pracy urządzenia T badanego urządzenia (elementu) jest zmienną losową o rozkładzie wykładniczym. Wówczas ![]()
gdzie ![]()
- intensywność awarii. W związku z tym dobrą aproksymantą (przybliżeniem) niezawodności jest funkcja (*) ![]()
. ponadto wiadomo N(t)=1-F(t) gdzie F jest dystrybuantą rozkładu wykładniczego. Własność zmiennej T określona wzorem (*)![]()
nazywamy wykładniczym prawem niezawodności .
II. Wielowymiarowe zmienne losowe
Niech dana jest przestrzeń probabilistyczna i zmienne losowe X1,X2…Xn określone na tej przestrzeni. Uporządkowany układ (X1,X2…Xn ) nazywamy n wymiarową zmienną losową lub wektorem losowym jeżeli dla każdego A przeciwobrazu uogólnionego przedziału ![]()
jest zdarzeniem losowym (X-iloczyn kartezjański).
Rozkład prawdopodobieństwa
Funkcję Px określoną wzorem ![]()
nazywamy rozkładem prawdopodobieństwa wektora losowego X, A![]()
![]()
, ![]()
- rodzina zbiorów borelowskich przestrzeni Rn
Dystrybuantą wyznaczoną przez rozkład prawdopodobieństwa Px nazywamy dystrybuantą n-wymiarowej zmiennej losowej (X1,X2…Xn ) lub w skrócie n wymiarową dystrybuantą. Zatem dystrybuantą jest funkcja określona wzorem ![]()
UWAGA
Szczególnym przypadkiem zmiennej n-wymiarowej jest zmienna dla n=2. Czyli zmienna dwuwymiarowa, oznaczamy ją (X1,X2) lub częściej (X,Y).
Dystrybuanta dla zmiennej dwuwymiarowej wyraża się wzorem:![]()
Aby funkcja rzeczywista dwóch zmiennych była dystrybuantą musi być funkcją niemalejącą przynajmniej lewostronnie ciągłą dla każdego x,y oraz ![]()
![]()
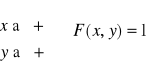
a także dla każdych (x1,y1), (x2,y2) takich ,że x1<x2 , y1<y2 musi zachodzić warunek ![]()
Typy wielowymiarowych zmiennych losowych
wielowymiarowe zmienne losowe typu skokowego
wielowymiarowe zmienne losowe typu ciągłego
Ad a.
N-wymiarowa zmienna losowa X jest typu skokowego jeżeli istnieje przeliczalny zbiór X taki , że ![]()
Px(X)=1 innymi słowy niech xi![]()
X ![]()
![]()
Szczególnym przypadkiem jest dwuwymiarowa zmienna losowa typu skokowego.
Dwuwymiarowa zmienna losowa (X,Y) typu skokowego przyjmuje skończoną lub przeliczalną liczbę wartości (xi , yk ) dla i=1,2…r , k=1,2,…m lub (i,k![]()
N) z prawdopodobieństwem pik=P(X=xi, Y=yk)
Def. Funkcji prawdopodobieństwa dla dwuwymiarowej zmiennej
Niech (xi , yk ) jest punktem skokowym zmiennej losowej (X,Y) typu skokowego. Prawdopodobieństwo tego, że zmienna losowa (X,Y) przyjmuje wartości (xi , yk ) nazywamy funkcję prawdopodobieństwa dwuwymiarowej zmiennej losowej typu skokowego. Przy czym:![]()
gdzie pik = P( X = xi, Y = yk )
Funkcję prawdopodobieństwa bardzo często zapisuje się w postaci tabeli :
X Y |
y1 y2 …yn |
x1 x2 . . . xn |
p11 p12 … p1m p21 p22 … p2m . . . pr1 pr2 … pr m |
Dystrybuanta dwuwymiarowej zmiennej losowej typu skokowego
![]()
Def. Zmienna losowa (X1,X2…Xn ) jest typu ciągłego jeżeli istnieje nieujemna funkcja f taka , że :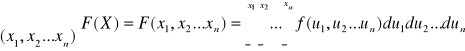
Funkcję nazywamy gęstością prawdopodobieństwa zmiennej (X1,X2…Xn )
Zatem funkcja gęstości musi być funkcją nieujemna i musi spełniać warunek: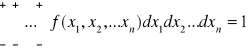
W punktach , w których f jest ciągła zachodzi 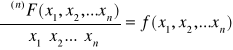
![]()
- pochodna cząstkowa
i ![]()
Dwuwymiarowa zmienna losowa typu ciąglego