Nazwiska Surzyński Tomasz Sycz Damian	GRUPA 9	ROK II	IMIR
Temat Rozwiązywanie równań różniczkowych z niezerowymi warunkami początkowymi

1.Cel ćwiczenia

-Zapoznanie się z różnymi metodami rozwiązań równań różniczkowych w Matlabie

-Wykorzystanie Simulinka do tworzenia modelu równania różniczkowego w Matlabie

2.Obliczenia

Rozwiązanie analityczne równania- x``+ 2x` + 4x = 0

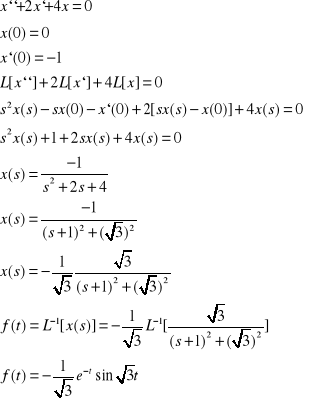
Wykres do metody analitycznej:

Rozwiązanie tego samego równania za pomocą programu Matlab

Tworzę plik „m”:

function xdot=funkcja(t,x)

% Układ rownan rozniczkowych

xdot=zeros(2,1);

xdot(1)=x(2);

xdot(2)=(-4*x(1)-2*x(2));

a następnie tworzę program ogólny rozwiązujący funkcję:

function rozw

t0=0;

clc

disp('Funkcja rozwiazuje rownanie rozniczkowe zwyczajne metoda ');

disp('Rungego - Kutty i podaje jego interpretacje graficzna');

disp(' ');disp('Postac rownania:');disp(' ');

disp(' x``+ 2*x`+ 4*x = 0');

x01=input ('Podaj wartosc x01 = ');

x02=input ('Podaj wartosc x02 = ');

tk=input ('Podaj czas symulacji tk = ');

x0=[x01 x02];

[t,x]=ode45('funkcja',t0,tk,x0,0.001,0);

plot(t,x(:,1),'r-');

xlabel('czas [s]');ylabel('amplituda sygnału');

title('Wykres rozwiazania rownania rozniczkowego');

grid;

Wykres:

Rozwiązanie równania x``+ 2x` + 4x = 0 w Simulinku

Buduję model:

Wykres:

Ogólne rozwiązanie umożliwiające rozwiązanie dowolnego równania różniczkowego:

t0=0;

clc

disp('funkcja rozwiazuje rownanie rozniczkowe metoda r-k');

a2=input('wspolczynnik przy x"= ');

a1=input('wspolczynnik przy x`= ');

a0=input('wpolczynnik przy x= ' );

ku=input('sila= ');

x01=input ('Podaj wartosc x01 = ');

x02=input ('Podaj wartosc x02 = ');

tk=input('tk = ');

x0=[x01 x02];

[t,x]=ode45('funkcja1',t0,tk,x0,0.001,0);

plot(t,x(:,1),'r-');

xlabel('czas[s]');

ylabel('amplituda sygnalu');

title('wykres rozw. rown. rozniczkowego');

grid;

function xdot=fukcja1(a0,a1,a2,t,x,ku)

xdot=zeros(2,1);

xdot(1)=x(2);

xdot(2)=(-(a0/a2)*x(1)-(a1/a2)*x(2)+(ku/a2));

Wnioski:

Na laboratorium uczyliśmy się rozwiązywać równania różniczkowe różnymi sposobami. Można stwierdzić, że wszystkie metody sprawdzają się dobrze. Liczą poprawnie i to jedynie czynnik ludzki wpływa na błędne wyniki. Matlab sprawdza się dobrze ale trzeba znać język programowania. Simulink jest niezłą “wtyczką” graficzną która znacznie ułatwia i przyśpiesza pracę.

---