Akademia Górniczo - Hutnicza w Krakowie						1. Zmysłowska Katarzyna 2. Trębacz Diana 3.Szewczyk Mateusz
Mechanika płynów
Wydział: GiG		Rok akademicki: 2008 / 09		Rok studiów: II		Kierunek: Inżynieria Środowiska	Grupa: 3/2
Temat ćwiczenia: Pomiar bezwymiarowego współczynnika oporu liniowego
Data wykonania:			Marzec 2009		Ocena:

1.Teoria:

Na podstawie odpowiedniego twierdzenia analizy wymiarowej można wykazać, że strata ciśnienia przy przepływie płynu przez rurę jest funkcją prędkości średniej v, średnicy przewodu D, jego długości L, chropowatości (bezwzględnej k lub względnej ε) ścianek przewodu, lepkości μ oraz gęstości ρ płynu. Funkcję tą można zapisać w postaci bezwymiarowej:

.

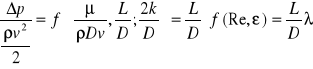
W zależności tej występują następujące wielkości bezwymiarowe:

- liczba Reynoldsa,

- chropowatość względna,

- bezwymiarowy współczynnik oporu liniowego.

Przy przepływach laminarnych współczynnik λ nie zależy od chropowatości i jest równy:

.

Przy przepływach turbulentnych w przewodach gładkich (ε = 0) współczynnik λ dla
3 ∙ 10³ < Re < 8 ∙ 10⁴ ze wzrostem liczby Reynoldsa maleje. Zależność λ = f (Re) aproksymuje:

.

Przy przepływach turbulentnych w przewodach chropowatych współczynnik λ jest
w ogólności funkcją liczby Reynoldsa i chropowatości: λ = f (Re,ε). Dla mniejszych liczb Reynoldsa współczynnik λ zależy zarówno od Re jak i od ε. Natomiast dla dużych liczb Reynoldsa λ zależy tylko od chropowatości względnej. W obszarze tym współczynnik λ jest równy:

.

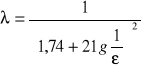
Stratę ciśnienia podaje wzór Darcy'ego - Weisbacha:

Zauważyć można, że pomiędzy stratą ciśnienia a prędkością przepływu przy ruchu laminarnym zachodzi zależność liniowa. Przekształcając powyższy wzór otrzymujemy zależność, z której można wyliczyć bezwymiarowy współczynnik oporu:

.

gdzie: Δp - liniowa strata ciśnienia w badanym przewodzie [Pa];

D - średnica badanego przewodu [m];

L - długość odcinka pomiarowego badanego przewodu [m];

ρ - gęstość powietrza [kg/m³];

v - średnia prędkość przepływu powietrza w badanym przewodzie [m/s].

2.Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie bezwymiarowego współczynnika oporu liniowego przy przepływie powietrza przez prostoosiową poziomą rurę o stałym przekroju.

3.Wykonanie ćwiczenia:

3.1.Współczynnik oporu liniowego:

gdzie:

D -średnica badanego przewodu, [m],

L -długość odcinka pomiarowego badanego przewodu, [m],

ρ -gęstość powietrza,
,

v_śr -średnia prędkość przepływu powietrza w badanym przewodzie,
,

3.2. Średnia prędkość przepływu powietrza:

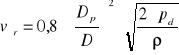
gdzie:

Dp -średnica przewodu z zainstalowaną sondą Prandtla, [m],

3.3. Liczba Reynoldsa:

gdzie:

v -kinematyczny współczynnik lepkości powietrza,
,

3.4. Różnice ciśnień mierzone manometrami cieczowymi:

1. U-rurka:

gdzie:

h₁, h₂ -wysokość słupków cieczy manometrycznej w ramionach U-rurki,

ρ_c1 -gęstość cieczy manometrycznej w U-rurce,
, ρ_c1=1000

g -przyśpieszenie ziemskie,
, g=9,81

3. Tabele obliczeniowe:

Tab.1.Parametry rur.

Rura żółta	Rura zielona
D=0,012 [m]	D=0,048 [m]
L=1,5 [m]	L=3,2 [m]
Dp=0,024 [m]
ν=16*10^-6

Tab.2. Zestawienie wyników obliczeń.

Δp [Pa]	pd [Pa]	Δp [Pa]	pd [Pa]	V śr [m/s]	V śr [m/s]	Re zolt	Re ziel	λ żółt	λ ziel
206,01	7	39	7	11,16516	2,434783	8373,872	7304,348	0,022992	0,17162
313,92	11	67	11	13,99627	3,826087	10497,2	11478,26	0,022295	0,119396
441,45	16	90	14	16,88014	4,869565	12660,11	14608,7	0,021555	0,099011
549,36	19	123	19	18,39471	6,608696	13796,03	19826,09	0,022589	0,073468
686,7	25	153	23	21,10018	8	15825,13	24000	0,021459	0,062364
843,66	31	187	27	23,49616	9,391304	17622,12	28173,91	0,021262	0,055311
981	36	230	33	25,32021	11,47826	18990,16	34434,78	0,021289	0,045541
1108,53	41	258	36	27,02141	12,52174	20266,06	37565,22	0,021123	0,042925
1255,68	49	295	41	29,54025	14,26087	22155,18	42782,61	0,02002	0,03784
1422,45	55	341	46	31,29662	16	23472,46	48000	0,020205	0,034749

4. Wykresy:

Rys.1. Wykres zależności współczynnika liniowego od wartości liczby Reynolds'a.

5. Wnioski:

Podczas pomiaru bezwymiarowego współczynnika oporu liniowego przy przepływie powietrza przez dwie rury o różnych średnicach stwierdzono, iż wraz ze wzrostem ciśnienia dynamicznego wzrastała średnia prędkość przepływu powietrza, zaś wartość współczynnika oporu liniowego spadała wraz ze wzrostem liczby Reynolds'a. Wraz ze wzrostem średnicy rury spada również wartość średniej prędkości, a wzrasta wartość oporu liniowego.

---