Część teoretyczna:

1. 
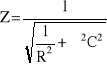
   Przewodnictwo elektryczne komórek i tkanek. Impedancja elektryczna komórki i tkanek. Parametry elektryczne błony komórkowej:
   Materiał biologiczny charakteryzuje się rzeczywistym oporem elektrycznym, czyli rezystancją i oporem pojemnościowym, nazywanym także oporem biernym lub reaktancją Opór wypadkowy przyjęto nazywać impedancja W przypadku obwodu złożonego ze źródła napięcia zmiennego, oporu R i pojemności C, połączonych szeregowo, całkowite napięcie przyłożone znajdujemy jako sumę wektorową obu spadków napięć. Napięcie na oporze R jest zgodne w fazie z natężeniem prądu, natomiast napięcie na kondensatorze jest opóźnione względem prądu o 1/4 okresu. Zatem impedancja tego obwodu wynosi:
   Kąt przesunięcia fazowego między natężeniem prądu a napięciem U znajdujemy ze związku :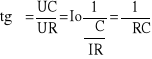
   
   
   
   Dla połączeń równoległych moduł impedancji wynosi:
   
   
   
   
   
   
   Natomiast tg kąta przesunięcia fazowego między napięciem U i natężeniem I znajdujemy ze wzoru:
   tg φ = Ic /I R=Ω CR
   Zależność częstotliwości impedancji lub tangensa φ tkanek może być wykorzystana jako charakterystyka ilościowa ich stanów fizjologicznych, względnie procesów patologicznych. Wyraźne zmiany przebiegu tych charakterystyk występują zwłaszcza przy działaniu na tkanki niektórych czynników fizycznych lub chemicznych (pole elektromagnetyczne, promieniowanie jonizujące itp.). Pomiary impedancji tkanek wykonuje się zazwyczaj przy użyciu mostków prądu zmiennego.

2. Kondensator w obwodzie prądu stałego i zmiennego:
   Kondensatorem nazywamy układ dwóch przewodników oddzielonych izolatorem (dielektrykiem). Wielkość charakteryzująca kondensator, to jego pojemność, czyli stosunek wartości ładunku, znajdującego się na jednej jego okładce, do napięcia między okładkami.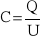
   
   
   
   
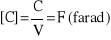
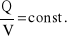
   Pojemność kondensatora płaskiego obliczamy ze wzoru: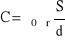
   
   
   …gdzie S to powierzchnia czynna okładek, d to odległość między nimi, ε₀ to przenikliwość elektryczna dla próżni a ε_r to względna przenikliwość elektryczna dielektryka między okładkami.
   Szeregowe łączenie kondensatorów: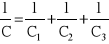
   
   
   Równoległe łączenie kondensatorów:
   C=C₁+C₂+C₃

3. Dielektryki:
   Dielektryk jest to izolator elektryczny, substancja w której praktycznie nie ma ładunków swobodnych w wyniku czego nie przewodzi ona prądu elektrycznego.
   Najważniejszą wielkością charakteryzującą dielektryki jest przenikalność elektryczna; przenikalność elektryczna dielektryków zależy od :

• częstotliwości zmian zewnętrznego pola elektrycznego

• temperatury

Zewnętrzne pole elektryczne może doprowadzić do niewielkiego przesunięcia ładunków związanych. Prowadzi to do polaryzacji dielektryków. Występują następujące rodzaje polaryzacji:

• polaryzacja elektronowa

• polaryzacja atomowa

• polaryzacja orientacyjna

• polaryzacja jonowa -międzyprzestrzenna
  

4. Zależność częstotliwości przenikalności i przewodności elektrycznej tkanek. Elektryczny model zastępczy tkanki:
   Zachowanie komórek w polu elektrycznym bywa różne w zależności od częstotliwości. Przy niskich częstotliwościach następuje, na skutek dużego oporu elektrycznego błony, separacja jonów we wnętrzu komórki. Zostaje indukowany silny dipol. Z tego powodu wartość przenikalności elektrycznej jest bardzo duża. Natomiast prawie wszystkie linie prądu omijają komórkę. Ze wzrostem częstotliwości efekt ten stopniowo maleje. Przy odpowiednio wysokich częstotliwościach (około 20 MHz) opór pojemnościowy błony zawiera praktycznie opór warstwy lipidowej i substancja wewnątrzkomórkowa bierze udział w przewodzeniu prądu. Polaryzacja jonowa komórki całkowicie znika.

• obszar α- dyspersji - obejmuje częstotliwości niskie od kilku herców do
  kilku kiloherców. Częstotliwość relaksacyjna (średnia) f ₀ np. dla tkanki
  mięśniowej wynosi około 100 Hz. Stwierdzono doświadczalnie że istnieje
  zależność między częstotliwością f₀ i promieniem R komórki.

• obszar β-dyspersji - występuje w zakresie częstotliwości od kilkudziesięciu kHz do ok. 30 MHz z częstotliwością średnią f ₀ = 1 MHz. Jej źródłem jest niejednorodna struktura tkanek. Wartość częstotliwości relaksacyjnej f o zależy głównie od wartości oporu elektrycznego i pojemności elektrycznej błon komórkowych.

• obszar γ - dyspersji - jest związany z relaksacjami dipolowymi niektórych struktur subkomórkowych i biocząsteczek oraz tzw. wody „związanej". Częstotliwości wody związanej leżą w granicach 10² - 10 ³ MHz. Relaksacja wody wolnej zachodzi dopiero przy częstotliwościach ok. kilkudziesięciu gigaherców. Wraz ze wzrostem częstotliwości znacznie zmienia się wartość przewodności własnej i względnej przenikalności elektrycznej tkanek. Należy podkreślić że dyspersja związana z wpływem błony komórkowej jest cechą charakterystyczną tylko komórek żywych. Przy obumieraniu tkanek jej opór elektryczny przy małych częstotliwościach maleje i zmniejsza się stopniowo dyspersja oporu. W analizie przewodzenia prądu zmiennego przez obiekty żywe symulujemy ich zachowanie się różnymi kombinacjami obwodów. Modele takie nazywamy elektrycznymi układami zastępczymi.

5. Potencjał spoczynkowy błony komórkowej:

Ujemny potencjał elektryczny występujący pomiędzy wnętrzem komórek tkanek pobudliwych

6. Pompa sodowo - potasowa:

Komórki pobudliwe mają różnice w stężeniu jonów Na+ i K+ na zewnątrz i wewnątrz komórki. Dzięki temu są komórkami pobudliwymi. Na zewnątrz jest więcej jonów Na+ a wewnątrz K+. Transportowane są one wbrew gradientowi stężeń z wykorzystaniem ATP poprzez enzym.

7. Impendencja naskórka:

Impedancja naskórka (skóry) w dużym stopniu zależy od stanu fizycznego naskórka (gruby, cienki, zdarty, suchy, wilgotny, mokry) i od powierzchni styku z zewnętrznym obwodem elektrycznym. Wartość impedancji naskórka nie jest stała i zależy od:

• wartości napięcia dotykowego,

• zatrzymaniem oddechu, zaburzeniami krążenia krwi

• wartości natężenia prądu,

• częstotliwości prądu,

• czasu przepływu prądu rażenia,

• temperatury i wilgotności skóry,

• powierzchni styku z przewodnikiem

• siły docisku przewodnika do naskórka

Wartość impedancji naskórka zawiera się w szerokich granicach - od kilkuset do kilkunastu tysięcy omów. Przy małych napięciach dotykowych (od 0 do 150 V) ma ona znaczny wpływ na impedancję ciała. W miarę wzrostu wartości napięcia wpływ ten jest coraz mniejszy, aż do pomijalnie małego przy napięciach większych niż 150 V. Rezystancja wewnętrzna ciała zależy głównie od drogi przepływu i jest największa przy przepływie prądu na drodze ręka - ręka i ręka - noga (stopa), przy czym jej wartość jest równa około kilkuset omów. Najmniejsza wartość impedancji jest na drodze przepływu prądu ręka - kark. Zależność impedancji naskórka od stopnia zawilgocenia skóry czy częstotliwości prądu też jest zmienna, a więc zmienna jest też impedancja ciała. Przy wilgotności względnej otaczającego powietrza powyżej 75% impedancja ciała nie zależy od impedancji naskórka i jest równa praktycznie tylko rezystancji wewnętrznej.

Cześć praktyczna:

1. Cel ćwiczenia:
   Zapoznanie z metodami badań biernych własności elektrycznych skóry ludzkiej.
   Impedancja elektryczna tkanek.

2. Pomiar impedancji Z oraz kąta przesunięcia fazowego φ dla częstotliwości f z zakresu (0,5 - 100) kHz.

3. Tabela wyników pomiarów:

Częstotliwość	Impedancja Z	Kąt φ	R	X
[kHz]	[Ω]	[°]	[Ω]	[Ω]
0,01	646	2	645,6065	22,54507
0,1	645	2	644,6071	22,51018
0,2	644	1	643,9019	11,23935
0,5	640	-3	639,1229	-33,495
0,8	630	-6	626,5488	-65,8529
1	624	-19	590,0036	-203,155
2	562	-21	524,6722	-201,403
5	382	-36	309,0445	-224,534
8	295	-39	229,2581	-185,65
10	253	-39	196,6179	-159,218
20	172	-28	151,867	-80,7491
50	143	-12	139,8751	-29,7314
100	138	-4	137,6638	-9,62639

R - część rzeczywista impedancji Z
R = Z * cos φ
X - część reaktancyjna impedancji Z
X = Z * sin φ

4. Wnioski:

Po analizie wyników i przedstawienia ich w formie wykresu widać, badany model skóry daje obraz impedancji, taki jak skóra ludzka. Krzywa impedancji kołowej przedstawiona w części teoretycznej ma swoje odzwierciedlenie w wykresie 2. Wykres 1 również zgadza się z teorią. Na podstawie wykresów widać charakterystykę właściwości elektrycznych skóry, które będąc osobniczo zmienne służą do badania np. uwodnienia skóry.

5. Wykresy:
   
   Wykres reaktancji X w funkcji składowej rzeczywistej R:
   
   
   



Wykres impedancji Z w funkcji częstotliwości:







Wykres kąta φ w funkcji częstotliwości:









---