Całkowanie numeryczne

1. Sformułowanie zagadnienia.

Przyjmijmy, że dla funkcji
należę wyznaczyć wartość całki oznaczonej

.

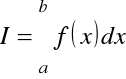
Jeśli znana jest funkcja pierwotna
, dla której
, to wówczas według wzoru Newtona-Leibnitza znajdziemy

.

Z dwóch powodów taka droga może być nie zrealizowana: trudno, albo niemożliwe, znaleźć funkcję pierwotną
; funkcja podcałkowa
wiadoma tylko w postaci tablicy.

Należę wrócić do początków. Pomijając niektóry szczegóły z analizy matematycznej wiadomo, że przybliżona wartość całki określa się przez sumę o postaci

,

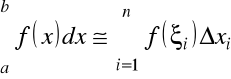
gdzie
są wartościami funkcji podcałkowej
w pewnych punktach środkowych
, a
.

Ten wzór nazywa się kwadraturą i związany jest z nazwiskiem Riemanna. Jest to suma pól odpowiednich prostokątów w interpretacji geometrycznej całki oznaczonej.

Bezpośrednio z tego wzoru wywodzi się znana metoda prostokątów. Algorytm tej metody przebiega następująco:

• przedział
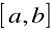
  dzielimy, np. na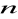
  równych odcinków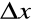
  ;

• wybieramy punkty
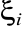
  np. jako końcowe, albo środkowe punkty, odpowiedniego podprzedziału i określamy wartości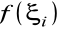
  ;

• obliczamy sumę całkową Riemanna.

Można mówić, że w przedziale
funkcja
została zastąpiona przez funkcję schodkową. Oto możliwa realizacja

,
.

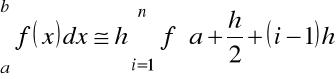
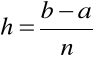
Inna metoda polega na tym, że funkcję podcałkową
zastępujemy pewną funkcję interpolującą
, dla której znalezienie funkcji pierwotnej nie przestawia problemu, mianowicie

.

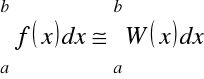
Mogą to być znane wielomiany Newtona, Gaussa, Lagrange'a czy funkcji sklejane.

2. Kwadratury Newtona-Cotesa.

Załóżmy, że funkcja podcałkowa
jest określona w przedziale
w równoodległych punktach

,
,
,
.

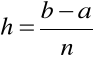
Wybierzmy wielomian Lagrange'a dla zastąpienia funkcji podcałkowej
, w szczególności

,
.

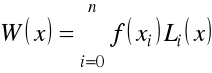
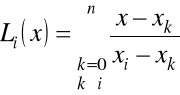
Dokonamy pewnego „chwytu organizacyjnego”. Określimy nowa zmienną

,
.

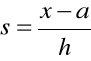
Kiedy zmienna
zmienia się od
do
z krokiem
, to zmienna
zmienia się od
do
z krokiem
.

Podstawimy

,
i

do wielomianu Lagrange'a

.

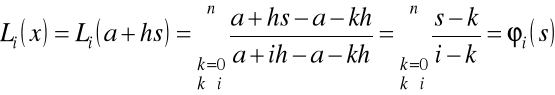
Zauważmy, że otrzymana wielkość zależę tylko od liczby węzłów.

Teraz dokonamy całkowania w proponowanym obliczaniu całki

.

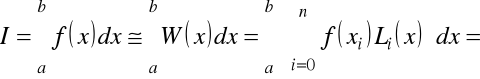
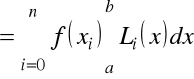
Zamiana zmiennej całkowania
prowadzi do

,

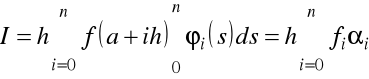
gdzie

i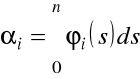
.

Otrzymaliśmy powszechnie znany wzór dla kwadratury Newtona-Cotesa

,
,
.

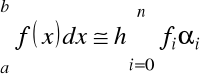
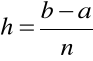
Współczynniki kwadratury
są liczbami wymiernymi i ich wartości tablicowane (nie zależą od funkcji i przedziałów całkowania).

Jako przypadki szczególne otrzymujemy, np.:

• 
  :
  ,
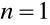
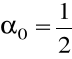
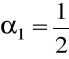
  (metoda trapezów);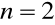

• 
  :
  ,
  ,
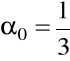
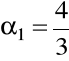
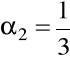
  (metoda paraboli Simpsona);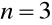

• 
  :
  ,
  ,
  ,
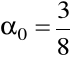
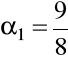
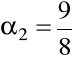
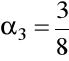
  (metoda „3/8”).

3. Metoda trapezów.

W metodzie trapezów funkcja podcałkowa
w przedziale
jest zastąpiona wielomianem pierwszego stopnia
. W tym przypadku współczynniki kwadratury są następujące
,
. Wówczas mamy

.

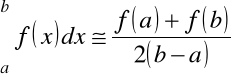
Dla praktycznego wykorzystania ten wzór stosujemy do każdego podprzedziału, np. otrzymanego z przedziału
dzieleniem przez
. Jego szerokość wynosi

,

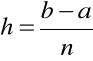
więc pole tego trapezu

.

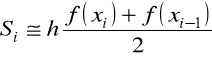
Ostatecznie otrzymamy

.

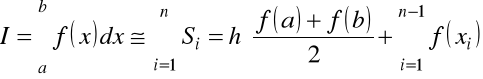
Interpretacja geometryczna jest oczywista (rys). Błąd bezwzględny

,

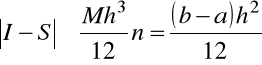
gdzie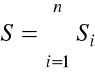
. Jednak w praktyce stosuje się powtarzanie obliczeń do osiągnięcia pożądanej precyzji.

4. Metoda paraboli (Simpsona).