Budownictwo Rok I
|
WYZNACZANIE MODUŁU YOUNGA |
30.03.2008 |
Ćw. nr 13 |
Alicja Wisełka |
|
1. Opis teoretyczny
Działanie sił zewnętrznych na ciało może wywołać odkształcenia, które polegają na przemieszczeniu cząsteczek z jednego położenia równowagi w inne. Istnieją dwa rodzaje odkształceń. W pierwszym przypadku siły zewnętrzne są słabsze od sił wewnętrznego oddziaływania międzycząsteczkowego i po zaprzestaniu działanie tych sił ciało wraca do stanu po przedniego. Jest to odkształcenie sprężyste. W drugim przypadku siły zewnętrzne są mocniejsze od międzycząsteczkowych i ciało ulega stałemu odkształceniu- odkształcenie plastyczne.
Wielkość fizyczną, równą liczbowo sile sprężystości F przypadającej na jednostkę powierzchni przekroju ciała, nazywamy naprężeniem σ.
Angielski fizyk R. Hooke stwierdził na drodze doświadczalnej, że naprężenie ciała sprężyście odkształconego jest proporcjonalne do względnego odkształcenia tego ciała:
![]()
k - współczynnik sprężystości zależny od właściwości materiału, z którego wykonane jest ciało,
ε - odkształcenie względne.
Wszystkie odkształcenia, jakim ulegają ciała, można podzielić na trzy główne grupy:
Jednostronne ściskanie lub rozciąganie,
Wszechstronne ściskanie lub rozciąganie,
Ścinanie,
Dla jednostronnego ściskania lub rozciągania z prawa Hooke'a wynika następujący wzór na wartość strzałki ugięcia dla pręta o długości l i przekroju w kształcie prostokąta o podstawie a i wysokości h.
![]()
E - moduł Younga dla danego materiału.
![]()
3. Obliczenia
Strzałkę ugięcia obliczyłam ze wzoru: ![]()
Dla pierwszego pierwszego prętu pierwszego pomiaru otrzymałam wartość strzałki: ![]()
=0,24[mm]
Otrzymałam następujące wartości strzałki ugięcia:
rodzaj pręta |
nr pomiaru |
obciążenie F[N] |
H1 [mm] |
H2 [mm] |
Hśr [mm] |
1 |
1 |
9,81 |
0,23 |
0,24 |
0,24 |
|
2 |
19,62 |
0,47 |
0,48 |
0,48 |
|
3 |
29,43 |
0,74 |
0,75 |
0,74 |
|
4 |
39,24 |
0,99 |
1 |
1 |
|
5 |
49,05 |
1,245 |
1,26 |
1,25 |
|
6 |
58,86 |
1,5 |
1,5 |
1,5 |
2 |
1 |
9,81 |
0,22 |
0,24 |
0,23 |
|
2 |
19,62 |
0,45 |
0,46 |
0,46 |
|
3 |
29,43 |
0,71 |
0,72 |
0,72 |
|
4 |
39,24 |
0,94 |
0,955 |
0,95 |
|
5 |
49,05 |
1,18 |
1,19 |
1,18 |
|
6 |
58,86 |
1,29 |
1,29 |
1,29 |
3 |
1 |
9,81 |
0,18 |
0,18 |
0,18 |
|
2 |
19,62 |
0,33 |
0,33 |
0,33 |
|
3 |
29,43 |
0,515 |
0,52 |
0,52 |
|
4 |
39,24 |
0,69 |
0,69 |
0,69 |
|
5 |
49,05 |
0,86 |
0,86 |
0,86 |
|
6 |
58,86 |
1,035 |
1,035 |
1,035 |
Następnie obliczyłam wartość wyrażenia F/H [N/m], które potrzebne mi będą w dalszych obliczeniach. Wyniki te zawarte są w tabeli głównej.
Moduł Younga obliczyłam ze wzoru: ![]()
![]()
Dla pręta pierwszego:
l = 0,305 m
a = 0,0197 m
h = 0,0047 m
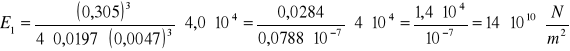
Natomiast dla pręta drugiego:
![]()
Dla pręta trzeciego:
![]()
Niepewności wyznaczyłam ze wzoru dla funkcji wielu zmiennych dla pomiarów pośrednich nieskorelowanych, który jest zawarty w skrypcie:
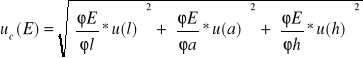
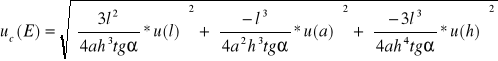
za wartość tgα przyjęłam wartość ΔH/ΔF
dla pręta I: tgα= 0,000026
dla preta II: tgα= 0,000022
dla pręta III: tgα= 0,000017
Dla pierwszego pręta otrzymałam wyniki:
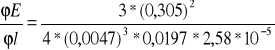
=3,7*10-15 u(l)=0,0305*10-3
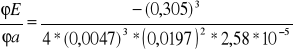
= -6,8*1012 u(a)= 0,0197*10-3
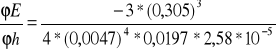
= -8,6*1013 u(h)= 0,0047*10-3
![]()
![]()
Dla drugiego pręta otrzymałam wyniki:
![]()
Dla trzeciego pręta otrzymałam wyniki:
![]()
Początek lini wykresów powinien mieć początek w punkcie (0,0) jednak z powodu błędów pomiarów rzecz ta wygląda inaczej.
Z wykresu wynika, że strzałka ugięcie jest wprost proporcjonalna do obciążenia siłą F. Wykres jest potwierdzeniem prawa Hooke,a. Wraz ze wzrostem siły strzałka ugięcia wzrasta, czyli wielkość odkształcenia jest proporcjonalne do obciążenia.
Z wykresu wynika, że największą wytrzymałość ma pręt III.
4.Wnioski
Wyznaczony moduł Younga, kolejno dla każdego pręta wynosi:
![]()
Wynik ten nie mieści się on podanych w tablicach przedziałach.
Najbliższy mu przedział to: 3400-12700*10-7 [nm] a odpowiadające mu ciało to cynk.
![]()
i mieści się on w przedziale: 7350-10300*10-7 [nm] więc jest to żelazo lane
![]()
i mieści się on w przedziale: 7800-12700*10-7 [nm] więc jest to miedź
Błędy mogą wynikać głównie z powodu:
niedokładności punktu 0 na śrubie mikrometrycznej;
ze wstrząsów pochodzenia zewnętrznego;
z niedokładności odczytu przyrządów;
z powodu niedoskonałości wycechowania odważników;
zaokrąglenia poszczególnych wartości,
tabela główna:
Rodzaj pręta |
Długość l [m] |
Krawędzie ai [m] |
Wartość srednia a [m] |
Krawędzie hi [m] |
Wartość srednia h [m] |
1 |
0,305 |
0,0195 0,0195 0,0200 |
0,0197 |
0,0045 0,0045 0,005 |
0,0047 |
2 |
0,155 |
0,0195 0,0195 0,0195 |
0,0195 |
0,003 0,003 0,003
|
0,003 |
3 |
0,458 |
0,0115 0,0115 0,0115 |
0,0115 |
0,0115 0,0115 0,0115 |
0,0115 |
rodzaj pręta |
nr pomiaru |
obciążenie F[N] |
H1 [mm] |
H2 [mm] |
Hśr [mm] |
F/H [N/m] *104 |
Wartość średnia F/H [N/m] |
E [N/m]
|
1 |
1 |
9,81 |
0,23 |
0,24 |
0,235 |
4,17 |
4,00 * 104 |
14 * 1010 |
|
2 |
19,62 |
0,47 |
0,48 |
0,475 |
4,13 |
|
|
|
3 |
29,43 |
0,74 |
0,75 |
0,745 |
3,95 |
|
|
|
4 |
39,24 |
0,99 |
1 |
0,995 |
3,94 |
|
|
|
5 |
49,05 |
1,245 |
1,26 |
1,25 |
3,92 |
|
|
|
6 |
58,86 |
1,5 |
1,5 |
1,5 |
3,92 |
|
|
2 |
1 |
9,81 |
0,22 |
0,24 |
0,23 |
4,3 |
4,2 * 104 |
7,5 * 1010 |
|
2 |
19,62 |
0,45 |
0,46 |
0,455 |
4,31 |
|
|
|
3 |
29,43 |
0,71 |
0,72 |
0,715 |
4,12 |
|
|
|
4 |
39,24 |
0,94 |
0,955 |
0,9475 |
4,141 |
|
|
|
5 |
49,05 |
1,18 |
1,19 |
1,185 |
4,139 |
|
|
|
6 |
58,86 |
1,29 |
1,29 |
1,29 |
4,56 |
|
|
3 |
1 |
9,81 |
0,18 |
0,18 |
0,18 |
5,4 |
5,7 * 104 |
7,8 * 1010 |
|
2 |
19,62 |
0,33 |
0,33 |
0,33 |
5,9 |
|
|
|
3 |
29,43 |
0,515 |
0,52 |
0,5175 |
5,687 |
|
|
|
4 |
39,24 |
0,69 |
0,69 |
0,69 |
5,7 |
|
|
|
5 |
49,05 |
0,86 |
0,86 |
0,86 |
5,7 |
|
|
|
6 |
58,86 |
1,035 |
1,035 |
1,035 |
5,687 |
|
|
Wyznaczanie modułu Younga. Alicja Wisełka
2.04.2008r
6
Wyszukiwarka