WSTĘP
Ponieważ chemia fizyczna stanowi poważny problem dla studentów, postanowiłam przygotować dla studentów kierunku Technologia Żywności i Żywienia Człowieka coś w rodzaju skryptu, obejmującego treść wykładu. Na początek trochę uwag na temat, jak należy uczyć się chemii fizycznej, bo czysto pamięciowa nauka nie zawsze przynosi pozytywne rezultaty.
Wykład jest wskazówką do tego, czego należy się nauczyć samodzielnie. Robiąc notatki nie skupiać się nad dokładnym przerysowaniem pokazywanych rysunków, a lepiej notować, co one oznaczają. W tym celu dostajecie na pierwszym wykładzie prezentacje pokazywane w trakcie wykładu. Najlepiej jest je sobie wydrukować i obok nich notować uwagi przekazywane na wykładzie. Proszę zwrócić uwagę, że niektóre rysunki są animowane i ich forma drukowana nie oddaje w pełni ich treści.
Ucząc się wyprowadzeń, zwracać uwagę na wstępne założenia, jaki układ w danym momencie opisujemy itp.
Wzory są nie po to, aby je zapamiętać same w sobie. Trzeba zawsze wiedzieć, do czego dany wzór służy, co opisuje i co oznaczają wielkości w nim występujące.
Nie uczyć się na pamięć rysunków w sposób fotograficzny.
Nauczyć się liczyć na własnym kalkulatorze.
W chemii fizycznej prawie każda wielkość posiada jednostki. Zwracać na nie baczną uwagę i zawsze zapisywać w odpowiednim miejscu. Zawsze przeprowadzać rachunek jednostek. Nigdy nie dodawać czy odejmować wielkości bez uzgodnienia najpierw jednostek. Pamiętajmy, że obowiązuje układ jednostek SI.
Pisząc kolokwium czy zdając egzamin dokładnie czytać treść poleceń.
Korzystać z polecanych podręczników, a nie ze skserowanych notatek wątpliwej jakości.
Jeśli będziecie każdy samodzielnie dla siebie pisać ściągi (których zresztą nie wolno używać), to jednak coś zostanie w głowie. Gdy będziecie korzystać ze skserowanych ściąg kolegów, to nie zostanie w głowie nic. Czyli ucząc się, robić sobie notatki !
Samodzielnie rozwiązywać zadania z arkusza, a nie korzystać z gotowych rozwiązań zrobionych przez nie wiadomo kogo.
Nauczyć się obsługi arkusza kalkulacyjnego Excel czy innego podobnego, co pomoże bardzo przy wykonywaniu sprawozdań z ćwiczeń laboratoryjnych.
Większość krążących pomiędzy studentami skserowanych ściąg, streszczeń wykładów itp. materiałów zawiera koszmarne błędy i uproszczenia. Ucząc się z takich pomocy nigdy nie zdacie egzaminu !
Wniosek - tylko samodzielna praca ze zrozumieniem przyniesie sukces.
Ponieważ mimo teoretycznie zaliczonej matematyki, większość z Was ma poważne problemy z matematyką, to na początek coś, co zatytułowałam “Niezbędnik matematyczny” czyli co bezwzględnie z matematyki musicie umieć, aby chemia fizyczna była dla was zrozumiała.
Niezbędnik matematyczny
Nie znajdą tu Państwo ścisłych definicji czy twierdzeń, ale przypomnienie pewnych wiadomości z matematyki, które są bardzo często wykorzystywane w chemii fizycznej i przy których popełniacie najwięcej błędów. Ich zapamiętanie i umiejętność stosowania uchroni Was przed mozolnym wbijaniem w pamięć wzorów, wyprowadzeń i wniosków, a pozwoli na swobodne posługiwanie się zależnościami opisującymi na przykład wpływ rozmaitych czynników na stany równowagi reakcji.
Potęgi i logarytmy
Działania na potęgach :
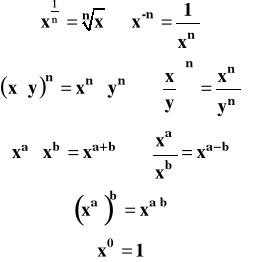
Działania na logarytmach :
Definicja : ![]()
Nigdy nie można wyciągać logarytmu z liczby ujemnej !!!!
![]()
Wśród logarytmów o różnych podstawach wyróżniamy :
Dziesiętne : ![]()
Naturalne : ![]()
gdzie e to podstawa logarytmów naturalnych ![]()
Wobec tego : 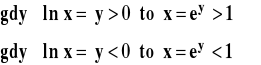
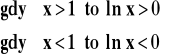
Przeliczanie logarytmów dziesiętnych na naturalne :
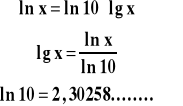
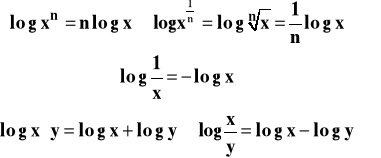
Funkcje i działania z nimi związane
Funkcja to sposób (podany wzorem, w postaci opisu słownego, tabeli bądź wykresu), w jaki jeden zbiór liczb (wartości funkcji) przyporządkowujemy drugiemu (argumenty funkcji).
![]()
W związku z tym, jeśli mamy polecone, narysować zależność y od x, to na osi poziomej zaznaczamy wartości x, a na osi pionowej y.
Funkcja liniowa :
![]()
a - współczynnik kierunkowy prostej
b - wyraz wolny
Współczynnik kierunkowy prostej to tangens kąta nachylenia tej prostej do osi poziomej (patrz rysunek).
W chemii fizycznej dokonujemy bardzo często zabiegu linearyzacji funkcji. Polega to na takim jej przekształceniu, że w efekcie otrzymamy zależność liniową.
Na przykład : Zależność stałej szybkości reakcji od temperatury opisuje wzór Arrheniusa : ![]()
. Aby dokonać linearyzacji, logarytmujemy obie strony przy podstawie naturalnej. Otrzymujemy :
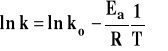
Oznaczamy : ![]()
Po porównaniu z równaniem prostej otrzymujemy : 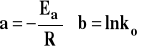
. Jeśli wykreślimy zależność lnk od 1/T, to otrzymamy linię prostą, której współczynnik kierunkowy, odczytany z wykresu jako tg, pozwoli na obliczenie Ea.
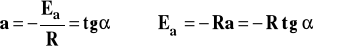
Funkcje mogą poddawane być pewnym przekształceniom - różniczkowaniu i całkowaniu. Różniczkowanie to wyznaczanie pochodnej funkcji, a całkowanie to znajdowanie funkcji pierwotnej (czyli funkcji, od której dana funkcja jest pierwszą pochodną).
Różne sposoby zapisu pierwszej pochodnej 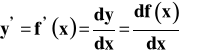
![]()
Różniczkowanie i całkowanie to dwie przeciwstawne czynności w matematyce i nie należy ich mylić i mieszać !!!!
Zakładam, że podstawowe zasady i wzory różniczkowania i całkowania Państwo znają, jeśli nie, trzeba to sobie koniecznie przypomnieć !!!!
Dla pamięci wzory, z którymi będziemy mieć najczęściej do czynienia:
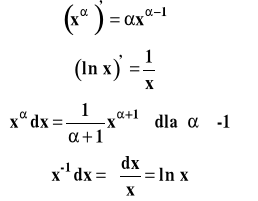
Rozróżniamy całki nieoznaczone i oznaczone.
Całka nieoznaczona jest funkcją pierwotną daną z dokładnością co do pewnej stałej C
![]()
Całkę oznaczoną (w granicach od x1 do x2) obliczamy jako przyrost wartości funkcji pierwotnej :
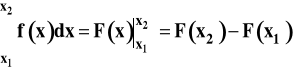
Wartość pierwszej pochodnej w danym punkcie (dla danej wartości argumentu xo) interpretujemy graficznie jako tangens kąta nachylenia stycznej do wykresu funkcji dla xo (patrz rysunek).
Całkę oznaczoną interpretujemy graficznie jako pole powierzchni zawartej pomiędzy wykresem funkcji, osią poziomą x i pionowymi liniami dla wartości argumentu x1 i x2 (patrz rysunek).
Funkcje mogą być rosnące lub malejące.
Funkcja rosnąca - gdy wartość argumentu rośnie, to wartość funkcji rośnie : ![]()
Funkcja malejąca - gdy wartość argumentu rośnie to wartość funkcji maleje : ![]()
To, czy funkcja jest rosnąca, czy malejąca poznajemy po znaku pierwszej pochodnej.
Jeśli wartość pierwszej pochodnej jest w pewnym przedziale argumentów dodatnia, to funkcja jest rosnąca w tym przedziale.
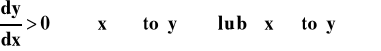
Jeśli wartość pierwszej pochodnej jest w pewnym przedziale argumentów ujemna, to funkcja jest malejąca w tym przedziale.
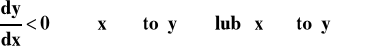
Jeśli wartość pierwszej pochodnej dla całego zakresu argumentów wynosi zero, to funkcja jest stała czyli jej wartość jest taka sama dla każdej wartości argumentu (nie zależy od wartości argumentu).
Jeśli wartość pierwszej pochodnej jest różna od zera, to wartość funkcji zależy od wartości argumentu.
Jeśli wartość pierwszej pochodnej w danym punkcie wynosi zero, to funkcja ma w nim ekstremum - maksimum bądź minimum.
Uwagi o stosowanych symbolach
Symbol (czytany „delta”) - oznacza przyrost (zmianę) o skończonej, określonej wartości
![]()
Symbol d (czytany „de”) - oznacza nieskończenie małą, różniczkową zmianę (różniczkę) danej wielkości
Nie wolno nigdy w jednym wzorze przyrównywać sobie, dodawać czy odejmować wielkości różniczkowych i przyrostów skończonych !!!!!
Na przykład taki zapis : ![]()
jest absolutnie niedopuszczalny !!!!!
Różniczka funkcji to : ![]()
Np. ![]()
Symbol d oznacza zawsze różniczkę zupełną.
Symbol đ oznacza różniczkę niezupełną.
Symbol ∂ stosujemy w notacji pochodnych cząstkowych funkcji wielu zmiennych.
Funkcja dwu zmiennych i jej różniczka
Jeśli mamy funkcję dwu zmiennych ![]()
, to jej różniczkę zapisujemy jako :
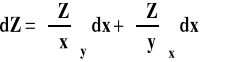
Jeśli ![]()
to 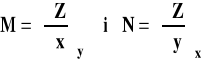
Różniczka funkcji dwu zmiennych jest różniczką zupełną wtedy i tylko wtedy, gdy drugie pochodne cząstkowe są sobie równe (warunek konieczny i wystarczający).
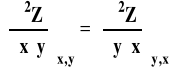
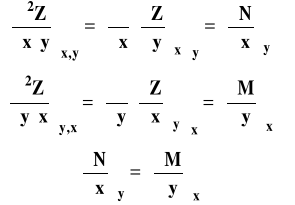
Obliczając całkę oznaczoną z różniczki zupełnej, możemy wyrażenie ją opisujące całkować osobno po poszczególnych zmiennych.
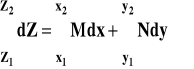
Polecane podręczniki
Peter Wiliam Atkins : „Chemia fizyczna” wyd. PWN, 2001
P.W. Atkins : “Podstawy chemii fizycznej”, wyd. PWN, 1999
Krzysztof Pigoń, Zdzisław Ruziewicz : “Chemia fizyczna”, wyd. PWN (różne wydania)
Jadwiga Demichowicz-Pigoniowa : “Obliczenia fizykochemiczne”, wyd. PWN, 1984, 1999
Lucjan Sobczyk, Adolf Kisza, Kazimierz Gatner, Aleksander Koll : “Eksperymentalna chemia fizyczna”, wyd. PWN, 1982
“Laboratorium z chemii fizycznej” pod redakcją Henryka Sugiera, wyd. Politechnika Łódzka, 1996
P.W. Atkins : "Chemia, Przewodnik po chemii fizycznej", wyd. PWN,1997
Małgorzata Przybyt, Henryk Sugier : “Obliczenia z chemii fizycznej”, wyd. Politechnika Łódzka, 1994
Alfabet grecki
alfa |
Α α |
Ni |
Ν ν |
beta |
Β β |
Ksi |
Ξ ξ |
gamma |
Γ γ |
omikron |
Ο ο |
delta |
Δ δ |
Pi |
Π π |
epsilon |
Ε ε |
Ro |
Ρ ρ |
dzeta (zeta) |
Ζ ζ |
Sigma |
Σ σ |
eta |
Η η |
Tau |
Τ τ |
theta |
Θ θ ϑ |
ypsilon |
Υ υ |
jota |
Ι ι |
Fi |
Φ φ ϕ |
kappa |
Κ κ |
Chi |
Χ χ |
lambda |
Λ λ |
Psi |
Ψ ψ |
mi |
Μ μ |
omega |
Ω ϖ ω |
Naprawdę radzę wszystkim Państwu opanować alfabet grecki, gdyż pozwoli to uniknąć wielu nieporozumień i błędów we własnych notatkach i pisaniu wzorów.
Dlaczego chemia fizyczna ?
Chemia fizyczna jest działem chemii zajmującym się poznaniem prawidłowości rządzących własnościami związków chemicznych, a w szczególności tymi, które przejawiają się w reakcjach pomiędzy nimi. Chemia fizyczna daje ilościowy opis własności związków chemicznych, zależności pomiędzy budową cząsteczek a ich własnościami i reaktywnością ; przemian fizycznych substancji i reakcji chemicznych. W sposób ilościowy pozwala przewidzieć, czy reakcja może zajść, jaki jest jej przebieg w czasie, jakie efekty cieplne, elektryczne itp. towarzyszą danej reakcji. W szczególności chemia fizyczna obejmuje trzy obszary :
Struktura i własności materii
Zmiany energii i stany równowagi przemian fizycznych i reakcji chemicznych
Przebieg procesów chemicznych w czasie i ich mechanizm
Chemia fizyczna bazuje na metodach pomiarowych rozwiniętych przez fizykę oraz na opisie teoretycznym pochodzącym z fizyki (szczególnie termodynamice, termodynamice statystycznej i mechanice kwantowej). Do pełnego zrozumienia chemii fizycznej niezbędna jest znajomość matematyki. W toku naszego wykładu w zasadzie będziemy bazować tylko na termodynamice, gdyż omawiamy tylko fragment zagadnień nazywanych chemią fizyczną. W zasadzie przedmiot powinien nosić nazwę „Wstęp albo elementy chemii fizycznej”.
Dlaczego musimy znać podstawy chemii fizycznej ?
Wyjaśnia i interpretuje obserwacje dotyczące fizycznych i chemicznych własności substancji
Jest bazą dla wszystkich innych działów chemii : nieorganicznej, organicznej, biochemii, analitycznej i innych
Daje ilościowy opis własności substancji i reakcji chemicznych
Jest bazą współczesnych technik analitycznych jak metody spektroskopowe, elektrochemiczne i inne
Jest podstawą metod pozwalających na poznanie struktury i własności cząsteczek chemicznych od najprostszych jak np. O2 do tak złożonych jak DNA.
Chemia fizyczna jest trudna, ale gdy ją zrozumiemy, to docenimy jej użyteczność !!!!
Chemia fizyczna jest z jednej strony nauką eksperymentalną, z drugiej - teoretyczną, dlatego też używamy w niej określonego toku rozumowania.
Najpierw jest zawsze doświadczenie (eksperyment) czyli pomiar ilościowy określonych wielkości czy też zależności.
Na podstawie wyników doświadczalnych formułowane są prawa sumujące dotychczas uzyskaną wiedzę.
Kolejnym etapem jest postawienie hipotezy czyli próby wytłumaczenia zaobserwowanych zjawisk na podstawie bardziej podstawowych założeń.
Kolejny etap to sformułowanie modelu czyli uproszczonej wersji systemu, zjawiska, które stanowią istotę rozpatrywanego problemu.
Na podstawie modelu formułuje się teorię, która powinna tłumaczyć dotychczas znane fakty (wyniki doświadczeń, prawa eksperymentalne) i przewidywać nowe.
Ostatnim etapem jest weryfikacja teorii przez doświadczenie czyli potwierdzenie nowych zjawisk przewidywanych przez teorię eksperymentalnie. Gdy wyniki doświadczenia nie zgadzają się z teorią, należy zbudować nowy model i nową teorię.
Ten sposób rozumowania i zdobywania wiedzy w chemii fizycznej doskonale ilustruje proces poznania własności gazów i ich opisu teoretycznego. Temu zagadnieniu poświęcony jest pierwszy dział wykładu.
Spis treści wykładu
Podstawowe informacje o gazach
Wprowadzenie do termodynamiki
Pierwsza zasada termodynamiki
Termochemia czyli praktyczne zastosowanie pierwszej termodynamiki do ciepeł reakcji chemicznych
Druga zasada termodynamiki i samorzutność procesów
Trzecia zasada termodynamiki
Termodynamika układów wieloskładnikowych
Reguła faz Gibbsa
Równowagi fazowe w układach jednoskładnikowych
Równowagi fazowe w układach dwuskładnikowych, prawo Raoulta, prawo Henry'ego
Roztwory rzeczywiste, pojęcie aktywności
Równowagi fazowe w układach trójskładnikowych, prawo podziału Nernsta
Własności roztworów rozcieńczonych
Równowaga reakcji chemicznych, sposób opisu, wpływ ciśnienia i temperatury
Opis termodynamiczny roztworów elektrolitów, solwatacja, tworzenie atmosfery jonowej, prawo Debye'a-Hückla
Konduktometria - ruch jonów w roztworze pod wpływem pola elektrycznego
Potencjometria - ogniwa galwaniczne
Kinetyka chemiczna - przebieg reakcji chemicznych w czasie, wpływ rozmaitych czynników na szybkość reakcji chemicznych
wartość funkcji
argument funkcji
x
y
![]()
b
x
y
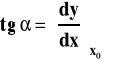
x
y
x2
x1
![]()
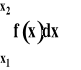
Wyszukiwarka