Ćwiczenia nr 6

Zadanie 1.

Na podstawie danych przykładowych Gretla (Gretl: mroz.gdt - Womans' labour force participation) zbuduj linowy model prawdopodobieństwa tego, że żona pracowała w 1975 roku (LFP). Jako zmienne objaśniające użyj:

• Liczbę dzieci w wieku do 6 lat

• Liczbę dzieci w wieku od 6 do 18 lat

• Wiek żony

• Liczbę lat edukacji żony

• Liczbę lat edukacji męża

• Liczbę lat edukacji matki żony

• Liczbę lat edukacji ojca żony

• Zmienną zerojedynkową wskazującą czy małżeństwo mieszka w dużym mieście

1. Które zmienne objaśniające są istotne?

2. Jak zinterpretujesz parametry przy zmiennych objaśniających?

3. Dodaj do modelu nową zmienną objaśniającą: płaca męża. Która ze zmiennych straciła na istotności i dlaczego?

4. Czy reszty modelu mają rozkład normalny?

5. Czy składnik losowy jest homoskedastyczny?

Zadanie 2.

Jeśli przyjmiemy, że prawdopodobieństwo jest dystrybuantą rozkładu logistycznego:

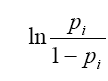
a. Ile wyniesie ?

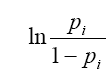
b. Dla jakiego p jest większy od zera?

Zadanie 3.

Oszacuj model logitowy ze zmienną zależną LFP oraz wszystkimi zmiennymi niezależnymi, które były wykorzystane w zadaniu 1.

1. Podaj interpretację parametrów modelu

2. Podaj interpretację efektów krańcowych

3. Czy test ilorazu wiarygodności wskazuje na istotność modelu?

4. Jaka jest miara trafności prognoz ex post?

Zadanie 4.

Oszacowano model ekonometryczny opisujący dwuczynnikową funkcję produkcji (Y - produkcja, L - praca, K - kapitał) i otrzymano następujące wyniki:

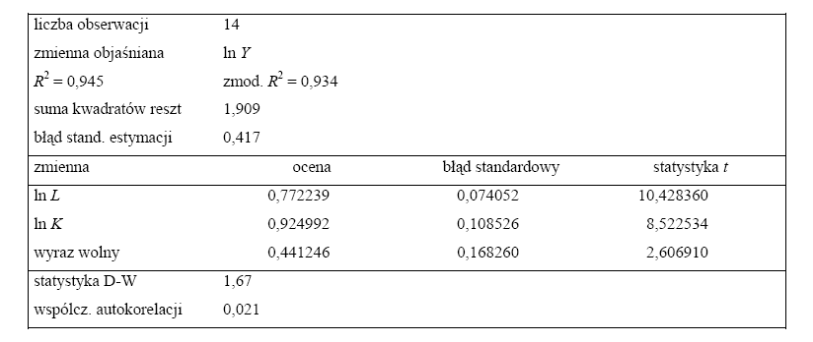
• a) jaka jest elastyczność produkcji względem kapitału?

• b) wyznacz krańcową produkcyjność pracy przy nakładach czynników równych L = 1,581 i K = 1,087;

• c) wyznacz prognozę zmiennej ln Y, jeśli wiadomo, że zmienne objaśniające w okresie pro-gnozy przyjmują wartości: ln L = -1,47 i ln K = -0,605

Zadanie 5 (egzaminowe przykład)

W dwóch firmach X i Y oszacowane funkcje produkcji:

Dla firmy X: P₁= 5,5Z^0,5M^0,5 Dla firmy Y: P₂= 4M + 2Z, gdzie

P - wielkość produkcji ( w tonach), Z - zatrudnienie (w etatach), M - liczba maszyn.

W badanym okresie w obu firmach zatrudnienie wynosiło 25 osób bezpośrednio pordukcyjnych, a liczba maszyn 16 sztuk.

1. Czy proces produkcyjny w firmie Y jest procesem produkcyjnym o stałych korzyściach względem skali? Odpowiedź uzasadnić.

2. Czy zwiększenie zatrudnienia o 1 etat, przy ustalonej liczbie maszyn, spowoduje mniejszy przyrost produkcji w firmie Y niż w firmie X? Odpowiedź uzasadnić.

3. Naszkicuj w układzie współrzędnych izokwanty obu funkcji produkcji dla poziom produkcji równego 22 tony.

4. Ile maszyn zastąpi 3 pracowników przy spełnionym warunku utrzymania wielkości produkcji na poziomie 16 ton? Podać odpowiedź z uzasadnieniem.

Zadanie 6. (egzamin 2008 luty)

Dana jest dynamiczna postać funkcji Cobba-Douglasa:

ln Y_t = lna + α₁lnK_t + α₂lnL_t + α₃t + lnξ_t

Y - wielkość produkcji w mln j.p.

K - kapitał wyrażony w mln j.p.

L - liczba zatrudnionych w tys.

Ponadto wiadomo, że

• wzrost kapitału o 1% skutkuje średnio ceteris paribus przyrostem produkcji o 0,8%

• przy stałych nakładach czynników wytwórczych, tempo wzrostu produkcji z okresu na okres wynosi średnio 0,02

• funkcja jest jednorodna stopnia 1,2

• izokwanta dla produkcji równej 300 przechodzi w roku t=1 przez punkt (K,L)=220,36)

1. Jakie jest oszacowanie parametru a1

2. Zapisz oszacowany model w postaci potęgowej

3. Wiadomo, że w roku t, na jednego zatrudnionego przypada 7 tys. j.p. kapitału. W tym roku przewiduje się zwolnienie dwóch tysięcy osób. Jaki musi być przyrost wielkości kapitału, żeby wielkość produkcji nie zmieniła się?

4. O ile procent wzrośnie produkcja w roku t+1 w porównaniu do roku t, jeśli wielkość zatrudnienia wzrośnie o 2 (nakłady kapitału bez zmian?

Zadanie 7.

W modelu logitowym oszacowanym dla zmiennej vote oznaczającej udział w wyborach (1=tak, 0=nie) mamy:

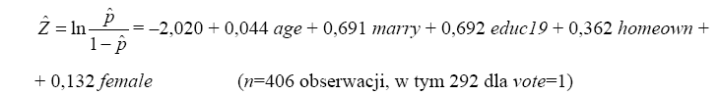
gdzie age jest wiekiem respondenta, marry oznacza stan cywilny: 1=zamężna/żonaty, 0 w pozostałych przypadkach, educ19=1 jeśli w wieku 19 lat respondent nadal się uczył (=0 w pozostałych przypadkach), homeown=1 jeśli miejsce mieszkania respondenta jest jego wła-snością (=0 w pozostałych przypadkach), female=1 dla kobiet, =0 dla mężczyzn.

• a) oblicz prawdopodobieństwo udziału w wyborach osoby żonatego mężczyzny z wyższym wykształceniem w wieku 45 lat, mającego własne mieszkanie; jak zmieni się to prawdo-podobieństwo za rok (age=46)?,

• b) oblicz ilorazy szans dla każdej ze zmiennych; o ile z każdym rokiem wieku respondenta zwiększa się szansa wzięcia udziału w wyborach?

• c) o ile procent zwiększa się szansa udziału w głosowaniu dla kobiety w porównaniu z męż-czyzną? o ile procent zwiększa się szansa udziału w głosowaniu dla osoby zamęż-nej/żonatego w porównaniu z innymi osobami?

• d) jaka jest prognoza zmiennej vote dla p = 0,65?

• e) zakładając, że głosować można od wieku 19 lat oblicz najmniejsze prawdopodobieństwo wzięcia udziału w głosowaniu; oblicz też prawdopodobieństwo największe przyjmując, że najstarszy respondent mógł mieć 80 lat.

Zadanie 7. (egzamin 2008 luty)

Na podstawie danych miesięcznych z okresu 201:05-2007:01 oszacowano model postaci

SS_t = a₀ + a₁UE_t + a₂ WOK_t + a₃WKP_t + a₄PSO_t

Gdzie SS to sprzedaż samochodów w Polsce, UE to zmienna zero-jedynkowa, która przyjmuje wartość 1 dla miesięcy członkostwa Polski w Unii Europeskiej, WOK to wskaźnik optymizmu konsumentów IPSOS, WKP to wskaźnik koniunktury w przemyśle GUS, zaś PSO to produkcja samochodów osobowych w sztukach. Wyniki estymacji powyższego modelu podane są poniżej.

Estymacjia KMNK z wykorzystaniem 69 obserwacji:

Zmienna Współczynnik Błąd standardowy

Const	37983,9	5103,07
UE	-11697	1425,71
WOK	-188,812	67,864
WKP	272,362	46,04
PSO	0,1622	0,039

Wsp. Determinacji R2 = 0,76

Statytyska F(4,64) = 50,933 (wartosc p<0,000001)

Statytyska Durbina_Watsona = 1,4953

Autokorelacja reszt rzędu pierwszego = 0,215

Test na normalność reszt -

Hipoteza zerowa: składnik losowy normalny

Statystyka testu: Chi-kwadrat(2) = 3,293 z wartością p=0,1927

Test RESET na specyfikację -

Hipoteza zerowa: specyfikacja poprawna

Statystyka testu: F(2,62) = 4,69 z wartością p= 0,0126

1. Na podstawie średnich względnych błędów szacunku oceń jakość wyników estymacji parametrów strukturalnych modelu

2. Na poziomie istotności 0,05 zweryfikuj hipotezę o łącznej istotności zmiennych objaśniających modelu

3. Czy na poziomie istotności 0,05 można przyjąć hipotezę o normalności rozkładu składnika losowego? Odpowiedź uzasadnij.

4. Wiedząc, że dla poziomu istotności 0,05 wartości krytyczne z rozkładu Durbina-Watsona wynoszą odpowiednio d_L=1,525 i d_U=1,703 oceń czy w modelu występuje autokorelacja składnika losowego. Odpowiedź uzasadnij.

Zadanie 9.

Na podstawie danych przekrojowych ze 100 gospodarstw domowych oszacowano parametry modelu logitowego, opisującego zależność posiadania w gospodarstwie komputera (KOM=1) od aktualnych miesięcznych dochodów (ZAROBKI) w złotych, liczby dzieci w gospodarstwie (DZIECI) i aktualnej przeciętnej ceny komputera w tys. zł.

Zmienna	Współczynnik	Błąd stand.	Statystyka t	Efekt rańcowy (dla średnich wartości zmiennych objaśniających)
Const	0,115	0,368	0,311
DZIECI	0,036	0,0586	0,619	0,008
ZAROBKI	0,0001	0,000067	2,31	0,0000381
CENA	-0,067	0,0235	-2,872	-0,01656

Test ilorazu wiarygodności: Chi-kwadrat(3)= 64 (wartość p=0,000)

McFaddena pseudo R kwadrat =0,25

Tablica trafności

Przewidywane

0 1

Empiryczne 0 33 10

1 10 47

1. Zinterpretuj oszacowaną wartość współczynnika przy zmiennej ZAROBKI oraz wartość efektu krańcowego z czwartej kolumny dla tej zmiennej.

2. Czy znaki ocen parametrów w modelu są zgodne z intuicją ekonomiczną? Odpowiedź uzasadnij.

3. Na podstawie obliczonych statystyk oceń prawdziwość hipotezy, że fakt posiadania przez gospodarstwo domowe komputera nie zależy od żadnej ze zmiennych DZIECI, ZAROBKI i CENA.

4. Dla wartości zmminnych objaśniających DZIECI=0, ZAROBKI=1000, CENA=1 policz logarytm ilorazu szans dla oszacowanego modelu logitowego. Co oznaczałoby iloraz szans równy 0,7 w tym modelu?

Zadanie 10.

Oszacowano funkcję produkcji

LnY = 0,4lnK + 0,7lnL

Y - wielkość produkcji w mln jp

K - nakłądy kapitału w mln jp

L - zatrudnienie w tys. pracowników

1. zinterpretuj otrzymane oszacowania parametrów tej funkcji

2. Podaj o ile musi zmienić się zatrudnienie, aby przy technicznym uzbrojeniu pracy wynoszącym 2 i wzroście nakładów kapitału o 1 mln jp wielkość produkcji pozostała na niezmienionym poziomie. Odpowiedź uzasadnij.

3. O ile procent wzrośnie wielkość produkcji, jeśli nakład kapitału i pracy wzrośnie o 30%. Odp. Uzasadnij

4. Wyznacz krańcowy produkt kapitału i pracy dla K=1 i L=3. Zinterpretuj uzyskane wyniki.

---