1. Czym się zajmuje kinematyka ?
Kinematyka zajmuje się opisem ruchu ciał bez uwzględnienia jego przyczyn, czyli sił. (jest wiec geometrią ruchu)
W kinematyce oprócz pojęć geometrycznych wprowadza się jeszcze
pojęcie czasu.
2. Jakie ciało nazywamy punktem materialnym ?
Punktem materialnym nazywamy takie ciało, którego wymiary w porównaniu z innymi
(w rozpatrywanym układzie) można pominąć.
3. Jakie są rodzaje toru ?
Tor prostoliniowy - ruch prostoliniowy
Tor krzywoliniowy - ruch krzywoliniowy
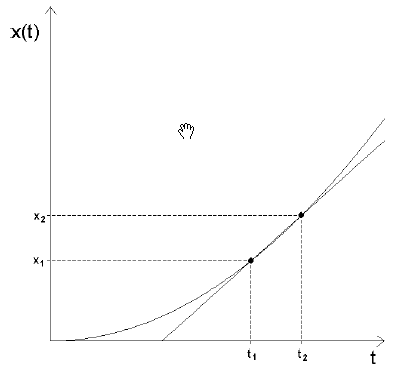
4. Co to jest prędkość ?
Prędkość jest to odcinek toru (droga) którą przebywa punkt
w jednostce czasu.
5. Co to jest przyspieszenie ?
Przyspieszenie jest to zmiana wektora prędkości w jednostce czasu.
Przyspieszenie ma zawsze zwrot do środka krzywizny toru.
6. Wzór na wartość liczbową prędkości ?
Wartość liczbowa prędkości wynosi:
Wzór na wartość liczbową przyspieszenia ?
Wartość liczbowa przyspieszenia wynosi:
8. Podział ruchu punktu w zależności od toru ?
a) krzywoliniowy
b) prostoliniowy
9. Podział ruchu punktu w zależności od prędkości ?
a) v rośnie - ruch przyspieszony
znak
równa się znakowi
b) v maleje - ruch opóźniony
znak
równa się znakowi
10. Podział ruchu punktu ze względu na współrzędną przyspieszenia stycznego?
a) a=0 ruch jednostajny
b) ruch jednostajnie zmienny
c) ruch zmienny
11. Podział ruchu w zależności od kierownic ?
a) przesunięcie - kierownice proste równoległe
(ruch ten określany jest przez ruch jednego punktu ciała sztywnego)
b) ruch postępowy - kierownice krzywe do siebie równoległe
(ruch określony jest przez ruch jednego punktu ciała) - np. ruch tłoka, klatka dźwigu
c) ruch obrotowy - kierownice dwóch punktów ciała redukują się do punktów i wyznaczają oś obrotu
d) ruch płaski - kierownice leżą w płaszczyznach do siebie równoległych. Chwilowy ruch płaski można traktować jako chwilowy obrót dookoła tzw. Osi chwilowego obrotu. Suma ruchów chwilowych oddaje nam zatem ruch płaski.
e) ruch kulisty - kierownice jednego z punktów redukują się do punktu
f) ruch ogólny - kierownice dowolnie zorientowane w przestrzeni
12. Ruch obrotowy ?
Nieruchome punkty A i B określają polożenie przechodzącej przez nie prostej
zwanej osią obrotu. Tor dowolnego punktu nie leżącego na osi obrotu jest
kołem.
Równanie ruchu obrotowego ciała sztywnego zapisujemy w postaci zależności kąta
obrotu od czasu:
13. Prędkość i przyspieszenie kątowe ?
Prędkość kątowa jest to granica ilorazu różnicowego przy t dążącym do zera
![]()
Zmienność w czasie prędkości kątowej nazywamy przyspieszeniem kątowym.
14. Prawa Newtona ?
I zasada dynamiki Newtona
Ciało pozostaje w stanie spoczynku lub w stanie stałej prędkości (zerowe przyspieszenie) gdy jest pozostawione samo sobie (działająca na nie siła wypadkowa jest równa zero)
a = 0, gdy Fwypadkowa = 0
gdzie: Fwypadkowa jest sumą wektorową wszystkich sił działających na ciało.
II zasada dynamiki Newtona
Tempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało.
![]()
(W definicji F mówimy o pojedynczej sile, a tu mamy do czynienia z siłą wypadkową.)
III zasada dynamiki Newtona
Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na drugie.
Trzecia zasada stwierdza, że w przypadku sił oddziaływania między dwoma ciałami
15. Zasada zachowania pędu ?
Jeżeli na jakiś układ ciał nie działają siły (oddziaływania) zewnętrzne, wtedy układ ten ma stały pęd.
Czyli, zapisując to wzorami:
jeżeli F = 0, to p = const
Lub jeszcze inaczej:
Zmienić pęd układu może tylko siła działająca z zewnątrz układu.
Zasada zachowania pędu może być traktowana jako alternatywna postać (sformułowanie) pierwszej zasady dynamiki Newtona, jako że omawiany przypadek braku siły zewnętrznej rozpatrywany jest w układzie inercjalnym
16. Kręt punktu materialnego ?
Moment wektora pędu punktu materialnego względem punktu O nazywamy krętem punktu materialnego względem punktu O.
![]()
czyli:
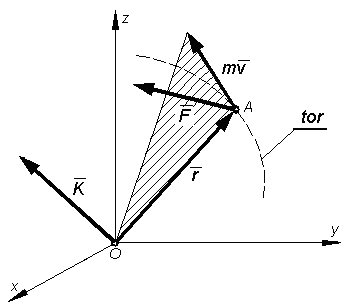
K= Mo(F)
Równanie to jest matematycznym zapisem prawa zmienności krętu punktu materialnego.
Pochodna krętu punktu materialnego względem danego bieguna równa jest momentowi sił działających na dany punkt względem tego bieguna.
17. Definicja i wzór na pracę ?
Praca siły F na przesunięciu elementarnym dr, lub inaczej pracą elementarną siły F nazywamy iloczyn skalarny wektora siły i wektora dr .
18. Od czego nie zależy praca sił ciężkości ?
Praca siły ciężkości nie zależy od kształtu toru po którym przesuwa się punkt jej przyłożenia
19. Definicja i wzór na moc ?
Mocą siły nazywamy stosunek elementarnej pracy wykonanej przez
te siłę do czasu , w którym ta praca została wykonana.
![]()
![]()
20. Energia kinetyczna ?
Energią kinetyczna punktu materialnego nazywamy połowę iloczynu jego masy
i kwadratu prędkości.
![]()
[E]=[N m]=[J]
21. Zasada zachowania energii mechanicznej ?
Prawo zachowania energii mechanicznej:
![]()
Energia mechaniczna punktu materialnego poruszającego się w polu potencjalnym ma wartość stała.
22. Co nazywamy wahadłem matematycznym ?
Wahadło matematyczne to punkt materialny zawieszony na nierozciągliwej i nieważkiej nici. Jest to idealizacja wahadła fizycznego.
Kiedy ciało wytrącimy z równowagi to zaczyna się ono wahać w płaszczyźnie poziomej pod wpływem siły ciężkości. Jest to ruch okresowy.
23. Co nazywamy wahadłem fizycznym ?
Wahadło fizyczne - dowolne ciało sztywne zawieszone tak, że może się wahać wokół pewnej osi przechodzącej przez to ciało
24. Wzór na częstość drgań ?
25. Definicja i wzór prawa powszechnego ciążenia ?
Dwie masy przyciągają się siłą proporcjonalną do iloczynu ich mas,
a odwrotnie proporcjonalną do kwadratu ich odległości.
![]()
m1,m2- masy ciał przyciągających się,
r- odległość miedzy masami,
G- stała ciążenia powszechnego (stała grawitacji).
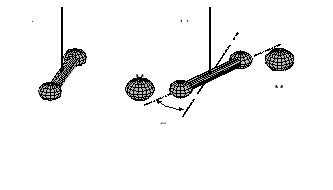
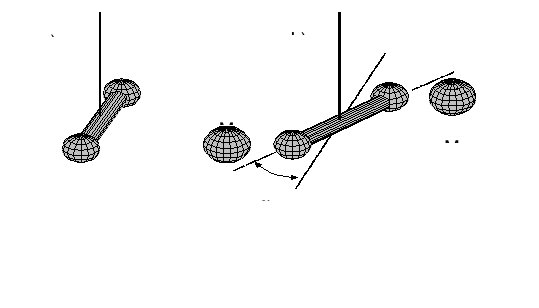
26. Opis doświadczenia Cavendisha ?
Cavendish chciał wyznaczyć stałą grawitacji G w laboratorium niezależnie od masy Ziemi i tym samym uniknąć błędu związanego z szacowaniem gęstości Ziemi.
Wykorzystał on fakt, że siła potrzebna do skręcenia długiego, cienkiego włókna kwarcowego o kilka stopni jest bardzo mała. Cavendish najpierw wykalibrował włókna,
a następnie zawiesił na nich pręt z dwiema małymi kulkami ołowianymi na końcach (rysunek a).
Następnie w pobliżu każdej z kulek umieścił większą kulę ołowianą i zmierzył precyzyjnie kąt o jaki obrócił się pręt (rysunek b).
Stała G została wyznaczona doświadczalnie przez Cavendisha przy pomocy tzw. wagi skręceń i wynosi:
Mając już godną zaufania wartość G, Cavendish wyznaczył Mz z równania:
![]()
27. Od czego nie zależy praca w polu grawitacyjnym ?
Wartość pracy w polu grawitacyjnym nie zależy od drogi
28. Potencjał pola grawitacyjnego ?
Potencjałem V pola grawitacyjnego w danym punkcie nazywamy stosunek pracy wykonanej przez siły tego pola przy przemieszczaniu masy z danego punktu w nieskończoność do wielkości tej masy.
Ep= m V
Ep - energia potencjalna
m - masa ciała
V - stała grawitacji
29. Na czym oparta jest mechanika relatywistyczna ?
Mechanika relatywistyczna oparta na szczególnej teorii względności (opracowanej przez Einsteina) - wykorzystuje się w zjawiskach atomowych, jądrowych i w astrofizyce gdzie prędkości są zbliżone do prędkości światła.
30. Transformacja Galileusza ?
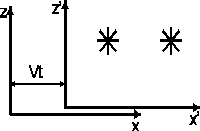
Dwa różne inercjalne
układy odniesienia,
poruszające się względem
siebie
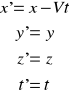
Wzory przekładające wyniki obserwacji jednego obserwatora na spostrzeżenia drugiego, równania noszą nazwę transformacji Galileusza.
31. Dylatacja czasu ?
Zjawisko dylatacji czasu jest własnością samego czasu i dlatego spowolnieniu ulegają wszystkie procesy fizyczne gdy są w ruchu. Dotyczy to również reakcji chemicznych, więc i np. biologicznego starzenia się.
32. Stałość przedziału czasoprzestrzennego ?
Wyobraźmy sobie pręt o dł. np. .20m. umieszczony w układzie współrzędnych w taki sposób, że rzut tego odcinka na oś x wynosi Δx, a na oś y Δy. Jeśli teraz ktoś znajdzie się w drugim układzie współrzędnych, obróconym względem pierwszego o kąt α, to spoglądając na ten odcinek z tego układu mierzy jego współrzędne jako Δx' i Δy'. Czy jest to dla nas dziwne? Oczywiście nie. Możemy także przetłumaczyć opis w jednym układzie na opis w drugim (znaleźć transformację)
Δx' =Δx cosα + Δy sinα
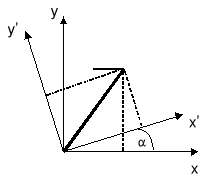
Δy'=-Δx sinα + Δy cosα
Poszczególne wyniki obserwacji Δx i Δy dla jednego człowieka, oraz, odpowiednio, Δx' i Δy' dla drugiego są różne, lecz suma ich kwadratów tj. długość pręta jest taka sama.
Szczególna teoria względności, że czas jest ściśle powiązany z odległością i naprawdę żyjemy w 4-wymiarowej przestrzeni; czasoprzestrzeni. Co więcej, podobna wielkość jak odległość w przykładzie też istnieje: jest nią przedział czasoprzestrzenny
który jest niezmiennikiem transformacji Lorenzta, czyli jest taki sam w dwóch układach.
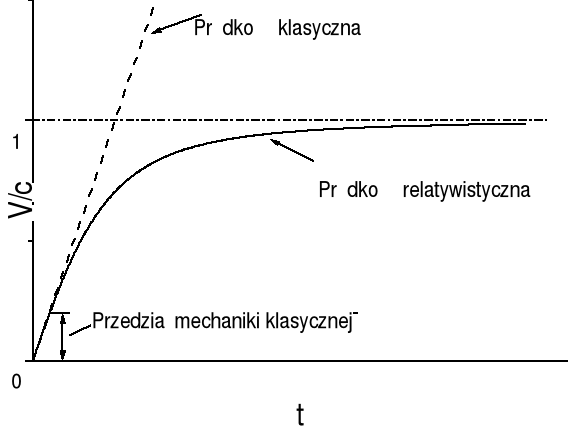
33. Różnice pomiędzy prędkością klasyczną a relatywistyczną ?
Porównanie zależności prędkości ciała od czasu działania siły w mechanice klasycznej i relatywistycznej jest pokazane na rysunku poniżej.
W przeciwieństwie do opisu klasycznego, z powyższej zależności wynika, że cząstki nie da się przyspieszać w nieskończoność działając stałą siłą.
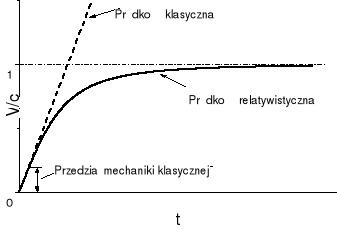
34. Równoważność masy i energii ?
Einstein pokazał, że zasada zachowania energii jest spełniona w mechanice relatywistycznej pod warunkiem, że pomiędzy masą i całkowitą energią ciała zachodzi związek:
![]()
gdzie m zależy od prędkości ciała V zgodnie z równaniem 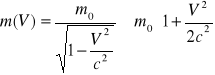
To znane powszechnie równanie Einsteina opisuje równoważność masy i energii. Wynika z niego, że ciało w spoczynku ma zawsze pewną energię związaną z jego masa spoczynkową:
![]()
Energię kinetyczną ciała poruszającego się z prędkością V obliczamy odejmując od energii całkowitej energię spoczynkową (nie związaną z ruchem):
![]()
Mechanika relatywistyczna wiąże energię kinetyczną z przyrostem masy ciała.
35. Definicja ruchu drgającego ?
Ruchem drgającym(drganiami) nazywa się każdy ruch, który charakteryzuje się powtarzalnością w czasie wielkości fizycznych określających ten ruch.
Ruch odbywa się po tym samym torze.
36. Definicja ruchu drgającego periodycznego ?
Ruchem drgającym periodycznym (drgania okresowe) nazywa się ruch wtedy, kiedy wartości wielkości fizycznych zmieniające się podczas drgań powtarzają się w równych odstępach czasu.
37. Definicja ruchu drgającego harmonicznego ?
Ruchem drgającym harmonicznie (drgania harmoniczne) nazywa się ruch wtedy, gdy wielkości fizyczne zmieniają się w czasie zgodnie z funkcjami harmonicznymi (sinus, cosinus). Ma to miejsce wtedy gdy działająca siła jest proporcjonalna do wychylenia i skierowana do położenia równowagi, określona np. prawem Hooke`a.
38. Siła harmoniczna definicja i wzór ?
Działającą na ciało siłę, która jest proporcjonalna do przesunięcia ciała od początku układu i która jest skierowana ku początkowi układu, nazywamy siłą harmoniczną lub siłą sprężystości.
F = - kx
gdzie x jest przesunięciem od położenia równowagi.
39. Drgania wymuszone ?

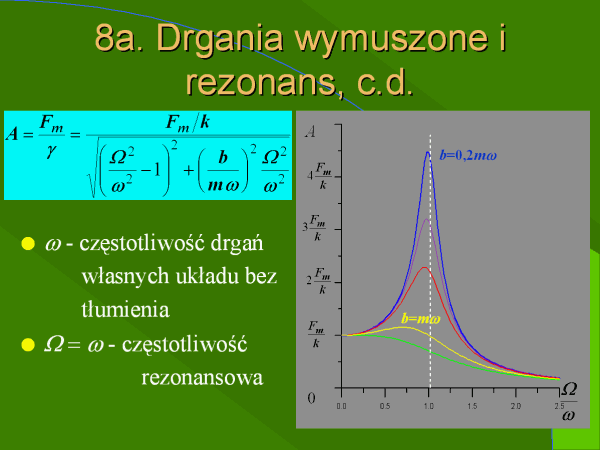
40. Rezonans ?
W szczególności gdy częstość siły wymuszającej osiągnie odpowiednią częstotliwość, to amplituda drgań może wzrosnąć gwałtownie nawet przy niewielkiej wartości siły wymuszającej. Zjawisko to nazywamy rezonansem.
41. Wzór na częstotliwość ?
f=1/T
T - okres
F - częstotliwość
42. Wzór na okres drgań ?
Funkcja cosၷt lub sinၷt powtarza się po czasie T dla którego ၷT = 2ၰ.
Ta szczególna wartość czasu jest zdefiniowana jako okres T :
T = 2ၰ/ၷ
Liczba drgań w czasie t jest równa:
n = t/T
43. Rodzaje fal ?
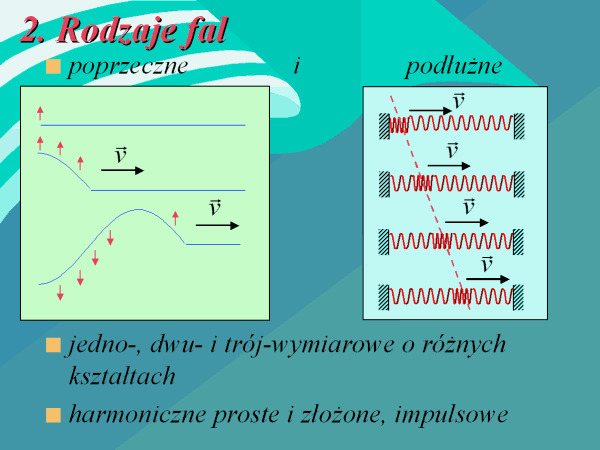
44. Zasada Huyghensa ?
Teoria Huyghensa oparta jest na konstrukcji geometrycznej (zwanej zasadą Huyghensa), która pozwala przewidzieć gdzie znajdzie się czoło fali w dowolnej chwili w przyszłości, jeżeli znamy jej obecne położenie.
Zasada ta głosi,że wszystkie punkty czoła fali można uważać za źródła nowych fal kulistych. Położenie czoła fali po czasie t będzie dane przez powierzchnię styczną do tych fal kulistych.
45. Prawo odbicia fal ?
Kąt padania jest równy kątowi odbicia.
Promień fali padającej, promień fali odbitej i prosta prostopadła (normalna) płaszczyzny odbijającej leżą w jednej płaszczyźnie.
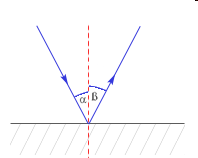
46. Prawo załamania fal ?
Stosunek sinusa kąta padania do sinusa kąta załamania, zwany współczynnikiem załamania n ośrodka drugiego względem pierwszego, jest równy stosunkowi prędkości rozchodzenia się fali w ośrodku pierwszym do prędkości rozchodzenia się fali w ośrodku drugim. w obu ośrodkach. Promień fali padającej, promień fali załamanej i prosta prostopadła (normalna) do granicy ośrodków leżą w jednej płaszczyźnie.
![]()
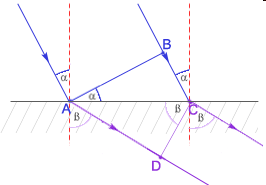
47. Zasada superpozycji ?
Wychylenie w danym punkcie jest sumą wychyleń wszystkich przebiegających przez ten punkt fal.
48. Fale stojące ?

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
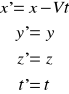
Wyszukiwarka