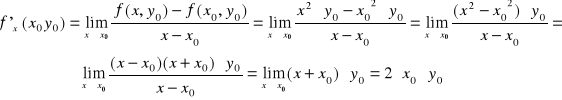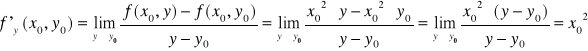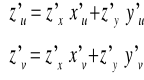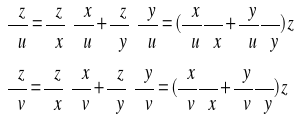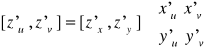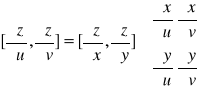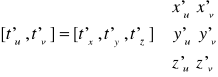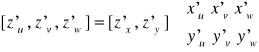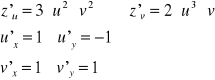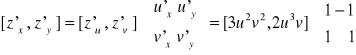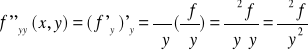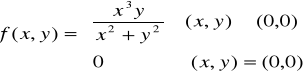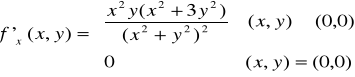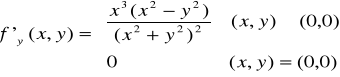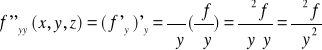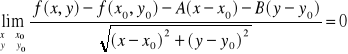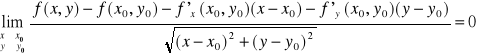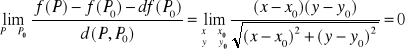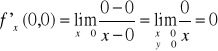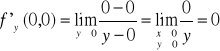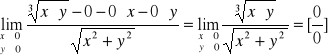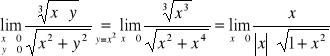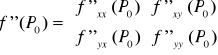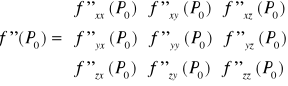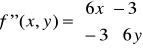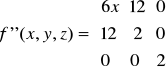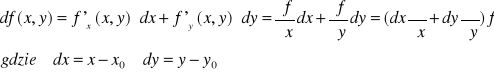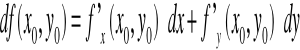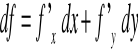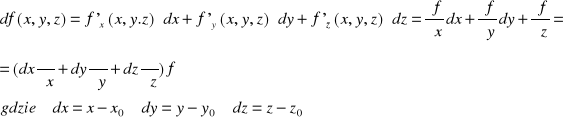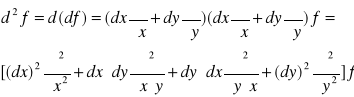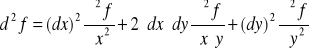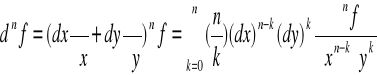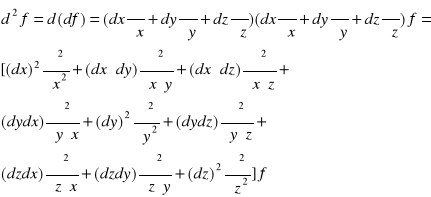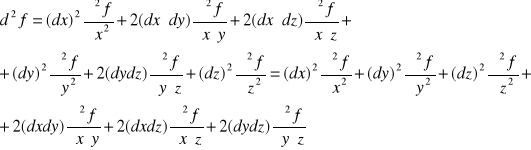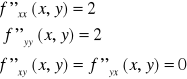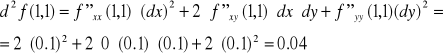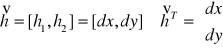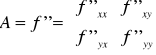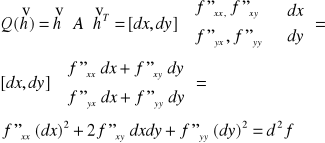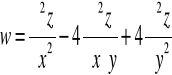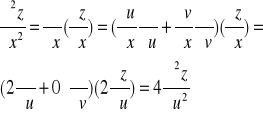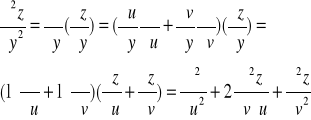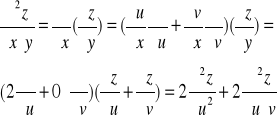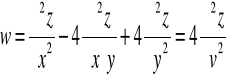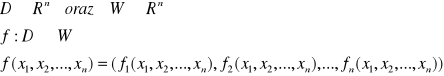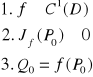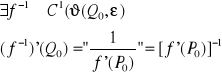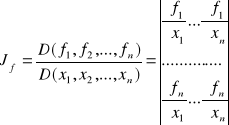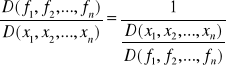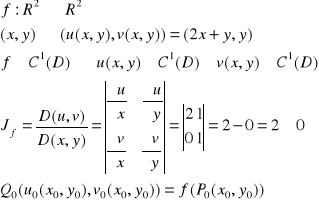AM2:WYKŁAD-2
|
|
Omówimy teraz sposoby obliczania pochodnych dla funkcji wielu zmiennych .
Rozważmy funkcję 2 zmiennych f(x,y) - jak zdefiniować pochodną dla takiej funkcji, przecież ma ona nie jeden a dwa argumenty. Przypomnijmy definicje pochodnej funkcji w punkcie dla funkcji jednej zmiennej f(x).
|
Ale jak przenieść tę definicję na funkcję dwóch zmiennych f(x,y) ?
Najprostszym sposobem jest ustalenie zmiennej y na określoną wartość (y=y0)
i wykonanie przejścia granicznego dla zmiennej x dla funkcji f(x, y0).
Podobnie możemy ustalić zmienną x na określoną wartość (x=x0) i wykonać przejście graniczne dla zmiennej y dla funkcji f (x0 , y).
Tak określone pochodne nazywamy pochodnymi cząstkowymi funkcji wielu zmiennych i opatrujemy indeksami dolnymi odpowiednio x i y żeby zaznaczyć jaki argument funkcji wielu zmiennych podlega zmianie.
Pochodne cząstkowe funkcji 2 zmiennych f(x,y) rzędu I
|
|
Jak można interpretować pochodne cząstkowe funkcji dwóch zmiennych ?
Równanie z=f(x,y) określa zazwyczaj pewną powierzchnię w przestrzeni trójwymiarowej. Ustalenie y=y0 oznacza dokonanie przecięcia tej powierzchni płaszczyzną y=y0 i uzyskanie w tej płaszczyźnie krzywej z=f(x,y0).
Rozważmy funkcję ![]()
opisującą w przestrzeni 3D powierzchnię paraboloidy obrotowej. Policzmy pochodną cząstkową w punkcie (1,2): ![]()
Przyjęcie y = 2 oznacza przecięcie tej paraboloidy płaszczyzną o wektorze normalnym [0,1,0] przechodzącą przez punkt (0,2,0). W przekroju dostajemy krzywą ![]()
czyli parabolę w układzie XZ jak widać na rysunkach poniżej.
Ten sam wynik dostaniemy jeżeli wystawimy w układzie XZ styczną do paraboli ![]()
w punkcie x=1 i znajdziemy jej tangens nachylenia.
Pochodna ![]()
oznacza tangens nachylenia tej krzywej w punkcie x0
i jest miarą lokalnej szybkości wzrostu funkcji f(x,y) względem zmiennej x przy ustalonej wartości y=y0.
Podobnie pochodna ![]()
oznacza tangens nachylenia krzywej z=f(x0,y)
w punkcie y0 i jest miarą lokalnej szybkości wzrostu funkcji f(x,y) względem zmiennej y przy ustalonej wartości x=x0.
Podobnie możemy określić pochodne cząstkowe rzędu I dla funkcji 3 zmiennych f(x,y,z) -w każdej granicy zmienia się tylko jedna zmienna a pozostałe zmienne są ustalone.
Pochodne cząstkowe funkcji 3 zmiennych f(x,y,z) rzędu I
|
|
Tutaj definiowaliśmy pochodne cząstkowe w konkretnym punkcie, ale możemy na tej bazie określić funkcję pochodną przyporządkowując każdemu punktowi wartość pochodnej cząstkowej w tym punkcie, co zapisujemy:
|
W każdym równaniu ostatnie dwa zapisy pochodnej cząstkowej są analogiczne do notacji Leibniza pochodnej funkcji jednej zmiennej w postaci ilorazu różniczek. Ostatni zapis to tak zwana postać operatorowa pochodnej cząstkowej.
Rozważmy kilka przykładów obliczania pochodnych cząstkowych wprost z definicji.
Przykład-1
Obliczmy pochodne cząstkowe funkcji
Pochodne te były liczone dla konkretnego punktu ale można to zapisać ogólniej:
Przykład-2
Obliczmy pochodne cząstkowe funkcji
w punkcie
co też można zapisać ogólnie:
|
Ponieważ pochodne cząstkowe funkcji wielu zmiennych liczymy jak pochodne funkcji jednej zmiennej ( przy pozostałych zmiennych ustalonych) to arytmetyka pochodnych cząstkowych jest analogiczna do arytmetyki pochodnej funkcji jednej zmiennej.
Arytmetyka pochodnych cząstkowych |
Podobnie wygląda arytmetyka pochodnych cząstkowych
|
Wniosek: |
Dla ilustracji zastosowania tych reguł rozważmy przykłady obliczania pochodnych cząstkowych na bazie tej arytmetyki.
Przykład-1
Obliczmy pochodne cząstkowe dla funkcji
Przykład-2
Obliczmy pochodne cząstkowe dla funkcji
|
Reguły arytmetyki stosują się do funkcji, która bezpośrednio zależy od zmiennych niezależnych x,y lub z. A jak wygląda reguła obliczania
pochodnych cząstkowych funkcji złożonej wielu zmiennych ?
Rozważmy funkcję z=f(x,y) w której zmienne x i y zależą od zmiennych u i v tak że możemy zapisać: x=x(u,v) oraz y=y(u,v).
Wówczas funkcja z=f(x(u,v),y(u,v))=z(u,v) i możemy liczyć pochodne cząstkowe względem tych zmiennych ![]()
według następującej reguły:
Jeżeli:
to wówczas: lub w zapisie operatorowym
Zapis indeksowy możemy przedstawić również w postaci macierzowej:
a tym samym zapis operatorowy ma postać macierzową:
Zauważmy, że mamy tutaj macierzowy odpowiednik pochodnej funkcji zewnętrznej oraz macierzowy odpowiednik pochodnej funkcji wewnętrznej.
Tak więc pochodna funkcji złożonej jest iloczynem macierzy pochodnej funkcji zewnętrznej i pochodnej funkcji wewnętrznej.
|
Postać macierzowa pozwala na łatwe uogólnienie na przypadki innej ilości zmiennych np.
Jeżeli
To wówczas:
|
lub w innym przypadku:
Jeżeli
To wówczas:
|
Rozważmy prosty przykład zastosowania powyższych wzorów.
Obliczmy pochodne cząstkowe funkcji
Wprowadźmy nowe zmienne u=x-y oraz v=x+y. Wówczas Obliczamy odpowiednie pochodne cząstkowe:
Nasz wzór na pochodne funkcji złożonej ma postać macierzową
Zatem
|
Rozważmy teraz pochodne cząstkowe ![]()
, ![]()
traktowane jako funkcje. Ponieważ każda z nich jest funkcją dwóch zmiennych możemy liczyć pochodne cząstkowe po zmiennej x i po zmiennej y tworząc w ten sposób pochodne rzędu drugiego.
Dla funkcji
czyli pochodną oraz po zmiennej y.
Należy zwrócić uwagę, że w zapisie indeksowym kolejność występowania zmiennych jest inna niż w zapisie operatorowym.
|
Dla funkcji
czyli pochodną oraz po zmiennej y.
Należy zwrócić uwagę, że w zapisie indeksowym kolejność występowania zmiennych jest inna niż w zapisie operatorowym
|
W ten sposób dla funkcji f(x,y) uzyskaliśmy 4 pochodne cząstkowe rzędu II.
Zauważmy również ze wśród tych pochodnych występują pochodne
w których następuje różniczkowanie :
po tej samej zmiennej (pochodne czyste)
po różnych zmiennych (pochodne mieszane)
Związek między pochodnymi mieszanymi różniącymi się kolejnością różniczkowania określa twierdzenie Schwarza:
Twierdzenie Schwarza o pochodnych mieszanych |
czyli jeżeli pochodne mieszane różniące się tylko kolejnością zmiennych są ciągłe w danym punkcie to są równe w tym punkcie
|
Podkreślmy, że nie wszystkie funkcje spełniają tę równość - można pokazać przykłady funkcji dla których równość pochodnych mieszanych w określonym punkcie nie jest prawdziwa.
Sprawdzimy czy dla funkcji:
obie pochodne mieszane II rzędu są równe w punkcie (0,0) tzn. czy zachodzi
Ponieważ
zatem musimy najpierw mieć zdefiniowane funkcje pochodne
Łatwo pokazać z definicji, że a poza punktem (0,0) pochodne cząstkowe I rzędu można obliczyć stosując arytmetykę pochodnych. Zatem otrzymujemy:
Teraz możemy już policzyć pochodne mieszane w punkcie (0,0).
a zatem dla naszej funkcji
Jednocześnie na podstawie twierdzenia Schwarza możemy wnioskować że przynajmniej jedna z pochodnych
|
Dalej będziemy zakładali, że nasze funkcje spełniają założenie twierdzenia Schwarza.
Wykażemy że dla funkcji
Liczymy najpierw pochodne cząstkowe I rzędu:
a potem pochodne cząstkowe II rzędu:
a zatem w każdym punkcie pochodne mieszane są równe
|
Rozważmy teraz jeszcze pochodne cząstkowe rzędu II dla funkcji 3 zmiennych.
Wiemy już że taka funkcja ma 3 pochodne cząstkowe rzędu I a w sumie dostaniemy 9 pochodnych cząstkowych rzędu II.
Dla funkcji
czyli pochodną po zmiennej y oraz po zmiennej z.
Należy zwrócić uwagę że w zapisie indeksowym kolejność występowania zmiennych jest inna niż w zapisie operatorowym
|
Dla funkcji
czyli pochodną
Należy zwrócić uwagę że w zapisie indeksowym kolejność występowania zmiennych jest inna niż w zapisie operatorowym.
|
Dla funkcji
czyli pochodną Należy zwrócić uwagę że w zapisie indeksowym kolejność występowania zmiennych jest inna niż w zapisie operatorowym. |
Również dla pochodnych mieszanych rzędu II funkcji 3 zmiennych f(x,y,z) stosuje się twierdzenie Schwarza i dalej będziemy zakładali że nasze funkcje mają pochodne mieszane równe.
|
W analogiczny sposób można tworzyć pochodne wyższych rzędów dla funkcji
2 zmiennych f(x,y) oraz 3 zmiennych f(x,y,z) ale wzory i ich zapis komplikują się znacznie i w tym wykładzie ograniczymy się do pochodnych rzędu II.
Warto też wiedzieć że twierdzenie Schwarza stosuje się też dla pochodnych rzędu III i wyższych np.:
|
Innymi słowami:
Uogólnione twierdzenie Schwarza |
Jeżeli pochodne cząstkowe mieszane dowolnego rzędu różniące się tylko kolejnością różniczkowania są ciągłe to są równe |
Z pojęciem pochodnych cząstkowych związane jest pojęcie klasy funkcji
wielu zmiennych.
Funkcja jest klasy w obszarze D
|
Pojęcie klasy funkcji upraszcza sformułowanie wielu twierdzeń.
Sformułujemy teraz pojęcie różniczkowalności funkcji. Rózniczkowalność funkcji w punkcie oznacza istnienie płaszczyzny stycznej do wykresu funkcji w tym punkcie.
Okazuje się że różniczkowalność funkcji nie jest zapewniona przez istnienie pochodnych cząstkowych natomiast jest zapewniona przez istnienie pochodnych cząstkowych ciągłych.
Związki miedzy ciągłością, istnieniem pochodnych cząstkowych i różniczkowalnością funkcji wielu zmiennych przedstawia tabela poniżej.
Ciągłość,pochodne cząstkowe, różniczkowalność |
|
1
|
Jeżeli f(x,y) ma w otoczeniu P0(x0,y0) pochodne cząstkowe rzędu I ograniczone to f(x,y) jest ciągła w P0
|
2 |
Jeżeli f(x,y) ma w otoczeniu P0(x0,y0) pochodne cząstkowe rzędu I ciągłe to f(x,y) jest ciągła w punkcie P0
|
3
|
Funkcja f(x,y) jest różniczkowalna w punkcie Po jeżeli istnieją liczby A i B takie że:
|
4 |
Jeżeli f(x,y) różniczkowalna w Po to jest ciągła w punkcie Po (warunek konieczny)
|
5 |
Jeżeli f(x,y) ma w otoczeniu Po(xo,yo) pochodne cząstkowe rzędu I ciągłe to f(x,y) jest różniczkowalna w Po (warunek dostateczny różniczkowalności)
Uwaga: samo istnienie pochodnych cząstkowych nie zapewnia różniczkowalności.
|
6 |
Jeżeli f(x,y) jest różniczkowalna w Po to istnieją pochodne
|
7
|
Funkcja f(x,y) jest różniczkowalna w Po(xo,yo) ⇔
|
Wprowadzając pojęcie przyrostów argumentów dx,dy,dz...dt oraz
różniczki df (P) w punkcie P dla funkcji wielu zmiennych f (x,y,z...t) jako:
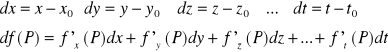
możemy napisać ogólną definicję różniczkowalności funkcji wielu zmiennych:
Funkcja f (P) jest różniczkowalna w punkcie Po ⇔ gdzie d (P,Po) - odległość między punktami P i Po
|
Omówimy teraz na przykładzie sposób określania czy dana funkcja jest różniczkowalna.
Wykażemy że funkcja
Liczymy kolejno:
a zatem funkcja nasza jest różniczkowalna w dowolnym punkcie.
|
Jak widać korzystanie z definicji jest dość trudne i czasochłonne.
Z poprzednich twierdzeń wynika że wystarczy obliczyć pochodne cząstkowe
i sprawdzić czy one są ciągłe - wtedy funkcja będzie różniczkowalna.
Rozważmy jako przykład funkcję ![]()
.
Pochodne cząstkowe tej funkcji: ![]()
![]()
Widać ze są one ciągłe w każdym punkcie (x,y) a więc w każdym punkcie funkcja jest różniczkowalna czyli w każdym punkcie istnieje płaszczyzna styczna do wykresu funkcji.
Na rysunku poniżej pokazano wykres funkcji ![]()
oraz płaszczyznę styczną do wykresu w punkcie (0,1,0)
Przedstawimy teraz przykład funkcji która posiada pochodne cząstkowe w danym punkcie ale nie jest w tym punkcie różniczkowalna.
Rozważmy funkcję
Ponieważ
a zatem pochodne cząstkowe w punkcie (0,0) istnieją .
Zbadajmy teraz różniczkowalność a więc granicę
Łatwo widać że granice iterowane są równe 0 zatem jeżeli istnieje granica podwójna to jest równa zero. Zweryfikujmy tę hipotezę. Rozważmy ciąg argumentów zbiegających do punktu (0,0) wzdłuż krzywej y = x2
Widać że w tym przypadku musimy badać granice obustronne - granica lewostronna = -1 a prawostronna = 1 zatem granica nie istnieje. Wnioskujemy zatem że funkcja nie jest różniczkowalna w punkcie (0,0) mimo że ma obie pochodne cząstkowe w tym punkcie ale nie są one ciągłe w punkcie (0,0).
|
Ważnym wnioskiem z powyższych rozważań jest fakt że różniczkowalność funkcji w punkcie zapewniona jest poprzez ciągłość jej pochodnych cząstkowych w tym punkcie.
Funkcja jest klasy
|
Opierając się na pojęciu różniczkowalności funkcji wielu zmiennych wprowadzimy jeszcze pojęcie pochodnej funkcji 2 zmiennych i 3 zmiennych użyteczne przy analizie ekstremów funkcji wielu zmiennych
Pochodne funkcji 2 zmiennych
Jeżeli funkcja f(x,y) jednokrotnie różniczkowalna w punkcie P0 to pierwszą pochodną funkcji w tym punkcie nazywamy macierz (macierz Jacobiego):
Jeżeli funkcja f(x,y) dwukrotnie różniczkowalna w punkcie P0 to drugą pochodną funkcji w tym punkcie nazywamy macierz (macierz Jacobiego):
Macierz ta jest macierzą symetryczną gdyż zakładamy spełnienie twierdzenia Schwarza.
|
Pochodne funkcji 3 zmiennych
Jeżeli funkcja f(x,y,z) jest jednokrotnie różniczkowalna w punkcie P0 to pierwszą pochodną funkcji w tym punkcie nazywamy macierz (macierz Jacobiego):
Jeżeli funkcja f(x,y,z) jest dwukrotnie różniczkowalna w punkcie P0 to drugą pochodną funkcji w tym punkcie nazywamy macierz (macierz Jacobiego):
Macierz ta jest macierzą symetryczną gdyż zakładamy spełnienie założenia twierdzenia Schwarza.
|
Zilustrujemy te pojęcia przykładami tworzenia macierzy I i II pochodnej.
Funkcja 2 zmiennych
Utwórzmy macierz I i II pochodnej dla funkcji w dowolnym punkcie (x,y).
Liczymy pochodne cząstkowe I rzędu:
zatem macierz I pochodnej w punkcie P(x,y) ma postać:
Liczymy teraz pochodne cząstkowe II rzędu:
zatem macierz II pochodnej w punkcie P(x,y) ma postać:
|
Funkcja 3 zmiennych
Utwórzmy macierz I i II pochodnej dla funkcji
Liczymy pochodne cząstkowe I rzędu:
zatem macierz I pochodnej w punkcie P(x,y) ma postać:
Liczymy teraz pochodne cząstkowe II rzędu:
zatem macierz II pochodnej w punkcie P(x,y,z) ma postać:
|
Przy definiowaniu różniczkowalności funkcji wprowadziliśmy pojęcie różniczki funkcji I rzędu dla funkcji o dowolnej ilości zmiennych.
Różniczka I rzędu daje nam pierwsze przybliżenie zmiany wartości funkcji przy niewielkich zmianach (przyrostach) argumentów funkcji wielu zmiennych
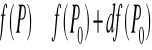
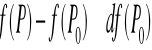
Skonkretyzujmy teraz tę definicję dla funkcji 2 zmiennych i dla funkcji 3 zmiennych.
Różniczka funkcji 2 zmiennych f(x,y):
Ostatni zapis różniczki to wygodny zapis pokazujący, jaki operator działa na funkcję f. Gdybyśmy chcieli obliczyć różniczkę funkcji w konkretnym punkcie to pochodne cząstkowe trzeba brać w tym punkcie.
Możemy też stosować krótszy zapis
|
Różniczka funkcji 3 zmiennych f(x,y,z):
Ostatni zapis różniczki to wygodny zapis pokazujący, jaki operator różniczkowy działa na funkcję f. Gdybyśmy chcieli obliczyć różniczkę funkcji w konkretnym punkcie to pochodne cząstkowe trzeba brać w tym punkcie.
Możemy też stosować krótszy zapis:
|
Możemy również tworzyć różniczki wyższych rzędów poprzez rekurencyjne
stosowanie operatora różniczki.
|
|
…..
|
|
Zobaczmy zatem jak wyglądają różniczki rzędu II dla funkcji 2 zmiennych i dla funkcji 3 zmiennych. Różniczka II rzędu daje nam drugie przybliżenie zmiany wartości funkcji przy niewielkich zmianach argumentów funkcji.
Dla funkcji 2 zmiennych f(x,y)
Uwzględniając że pochodne mieszane różniące się kolejnością zmiennych są równe (tw. Schwarza) otrzymujemy ostatecznie:
W powyższych wzorach wykonujemy mnożenie wyrażeń algebraicznych zawierających operatory różniczkowe a potem mnożenie operatorów zastępujemy składaniem operatorów różniczkowych.
Możemy zatem dla funkcji 2 zmiennych wykorzystując wzór dwumianowy Newtona wyprowadzić ogólny wzór na różniczkę rzędu n.
|
Dla funkcji 3 zmiennych f(x,y,z)
Przyjmując założenie o równości pochodnych cząstkowych otrzymamy:
|
Zilustrujmy powyższe wzory przykładem.
Obliczmy różniczkę rzędu I i rzędu II dla funkcji
Ponieważ
i wtedy wzór na różniczkę rzędu I wygląda następująco:
Ponieważ
liczymy pochodne cząstkowe rzędu II i podajemy wzór różniczki rzędu II:
|
Twierdzenie Taylora dla funkcji wielu zmiennych
Jeżeli funkcja f(P) jest klasy
czyli inaczej mówiąc:
lub jeszcze prościej: f(P) = (wartość przybliżona) + (błąd przybliżenia)
Przybliżenia dokonujemy za pomocą wielomianu stopnia n wielu zmiennych a błąd przybliżenia ma własność:
Jeżeli wszystkie pochodne cząstkowe rzędu (n+1) mają wspólne ograniczenie M
w
Dla ustalonego punktu P błąd przybliżenia będzie coraz mniejszy dla coraz większej wartości n, tak więc uwzględniając w powyższym wzorze różniczki wyższych rzędów uzyskujemy lepsze przybliżenie wartości f(P). Najczęściej używamy pierwszego lub drugiego przybliżenia. Oszacowania błędu są dla funkcji wielu zmiennych zazwyczaj dość złożone, więc tutaj je pomijamy.
Pierwsze przybliżenie uzyskamy za pomocą różniczki rzędu I :
Drugie przybliżenie uzyskamy za pomocą różniczki rzędu I oraz II :
|
Przykład-1
Obliczmy przybliżoną wartość funkcji rzędu.
Stosujemy wzór przybliżony: i liczymy kolejno:
Jednocześnie jest to wartość dokładna bo wyższe pochodne są równe 0.
|
Przykład-2
Oblicz przybliżoną wartość wyrażenia
Z postaci wyrażenia wynika, że jest to wartość funkcji
Stosujemy wzór przybliżony:
|
Rozważymy jeszcze na koniec przydatne pojęcie formy kwadratowej. Terminu tego będziemy używali przy omawianiu warunku koniecznego ekstremów warunkowych (związanych ) funkcji wielu zmiennych.
Formą kwadratową n zmiennych
Tak więc forma kwadratowa określona jest przez macierz symetryczną A. Zatem określoność macierzy symetrycznej (dodatnia,ujemna) może być równoważnie definiowana jako określoność formy kwadratowej.
Jeżeli wprowadzimy oznaczenie
|
Jako przykład zobaczymy teraz jak różniczkę rzędu II funkcji 2 zmiennych można przedstawić jako formę kwadratową przyrostów dx,dy.
Wprowadzamy oznaczenia:
i otrzymujemy:
Zakładamy tutaj równość pochodnych mieszanych.
|
W wielu zagadnieniach matematyki i fizyki występują wyrażenia zawierające pochodne cząstkowe jakiejś funkcji i mogą one w ogólności być dość skomplikowane. Okazuje się że uproszczenie takich wyrażeń może nastąpić za pomocą zamiany zmiennych niezależnych (nowe współrzędne).
Przykład: Wyrazimy wyrażenie różniczkowe w dla funkcji z=f(x,y)
wprowadzając nowe zmienne:
Ponieważ
Liczymy odpowiednie pochodne cząstkowe funkcji złożonej:
|
W powyższym przykładzie mając zależności ![]()
między starymi zmiennymi x,y a nowymi zmiennymi u,v
znaleźliśmy zależności odwrotne: ![]()
.
Powstaje pytanie czy zawsze uda się odwrócić te zależności ?
Odpowiedź na to daje następujące twierdzenie.
Twierdzenie o lokalnej odwracalności odwzorowań
|
Niech:
Jeżeli:
to wówczas:
Zapis
Jak widać z tego twierdzenia odwzorowanie odwrotne jest określone w otoczeniu punktu a więc tylko lokalnie .
|
Uwagi do twierdzenia:
Ciągłość odwzorowania:
Jakobian odwzorowania
Podstawowe własności jakobianów:
|
Przykład odwzorowania:
A zatem odwzorowanie f(x,y) jest odwracalne w każdym punkcie (x,y).
|
Autor: Wojciech Drabik (PJWSTK)
28
Wyszukiwarka