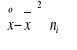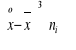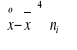Ćwiczenia kontrolne 1
Ćwiczenia z liczenia wskaźników opisu statystycznego dla danych jakościowych.
Przykład nr 1
Klasyfikacja zupełna i rozłączna grupy 30 osób ze względu na typ zachowań ingracjacyjnych:
a |
b |
c |
d |
Razem |
7 |
13 |
3 |
7 |
N = 30 |
podkreślanie własnych walorów;
podkreślanie walorów partnera interakcji;
pomniejszanie własnej wartości;
konformizm.
Polecenia:
Określić skalę pomiarową cechy.
Wskazać kategorię modalną.
Policzyć i zinterpretować częstość kategorii modalnej.
Wyznaczyć i zinterpretować dyspersję względną klasyfikacji.
Odpowiedzi:
Cechą mierzoną jest typ zachowań ingracjacyjnych sklasyfikowany na 4 kategorie - cecha wyrażona jest na skali nominalnej.
Kategorię modalną stanowi 13 osób podkreślających walory partnera interakcji.
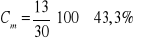
. Osoby zaliczone do kategorii b stanowią 43,3% próby badanej. Ich dominacja w próbie jest umiarkowana.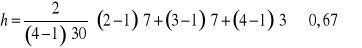
. Dyspersja klasyfikacji świadczy o umiarkowanie silnym zróżnicowaniu próby badanej ze względu na typ przejawianych zachowań ingracjacyjnych.
Przykład nr 2
|
p |
n |
s |
6 |
30 |
m |
18 |
12 |
Badano zależność między wiekiem (starsi, młodsi) a oceną graffiti (pozytywna, negatywna).
Polecenia:
Wyznaczyć 2. Obliczyć i zinterpretować Yule'a, V Cramera, T Czuprowa oraz współczynnik siły związku rp.
Odpowiedzi:
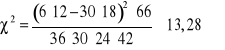
; ![]()
; 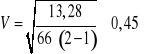
; 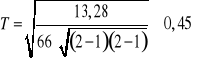
; 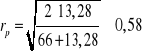
W badanej próbie 66 osób wystąpiła umiarkowana zależność między wiekiem a oceną graffiti. Zależność polega na tym, że częściej zdarzają się osoby starsze wypowiadające się krytycznie i osoby młodsze wypowiadające się pozytywnie.
Przykład nr 3
Badano zależność między typem ingracjacji (4 kategorie) a statusem społecznym (wysoki, umiarkowany, niski). Wiadomo, że dla próby 120 osób uzyskano 2 = 14,11. Wyznaczyć wskaźniki zależności.
![]()
; 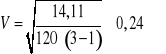
; 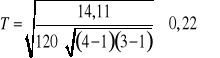
; 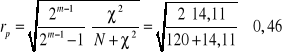
W badanej próbie 120 osób wystąpiła słaba zależność badanych cech (współczynnik rp wskazuje na zależność o umiarkowanej sile).
xi |
xi -x |
(xi -x)2 |
(xi -x)3 |
(xi -x)4 |
1 |
-3,55 |
12,60 |
-44,74 |
158,82 |
2 |
-2,55 |
6,50 |
-16,58 |
42,28 |
3 |
-1,55 |
2,40 |
-3,72 |
5,77 |
4 |
-0,55 |
0,30 |
-0,17 |
0,09 |
4 |
-0,55 |
0,30 |
-0,17 |
0,09 |
4 |
-0,55 |
0,30 |
-0,17 |
0,09 |
4 |
-0,55 |
0,30 |
-0,17 |
0,09 |
4 |
-0,55 |
0,30 |
-0,17 |
0,09 |
7 |
2,45 |
6,00 |
14,71 |
36,03 |
8 |
3,45 |
11,90 |
41,06 |
141,67 |
9 |
4,45 |
19,80 |
88,12 |
392,14 |
50 |
-0,05 |
60,70 |
78,00 |
777,16 |
Przykład nr 4
Grupę 11 osób zapytano o liczbę przeczytanych książek: 1, 2, 3, 4, 4, 4, 4, 4, 7, 8, 9.
Polecenia:
Określić rodzaj danych i skalę pomiarową cechy.
Wyznaczyć i zinterpretować wskaźniki położenia.
Wyznaczyć i zinterpretować wskaźniki rozproszenia.
Wyznaczyć i zinterpretować wskaźniki asymetrii.
Wyznaczyć i zinterpretować wskaźniki skupienia i koncentracji.
Odpowiedzi:
Dane indywidualne, cecha skokowa wyrażona na skali stosunkowej.
Dominanta: D = 4 Typowe dla tej grupy jest przeczytanie czterech książek.
Pozycja mediany: ![]()
Mediana: Me = 4 Połowa grupy przeczytała co najwyżej 4 książki (4 lub mniej) oraz połowa grupy przeczytała co najmniej 4 książki (4 lub więcej).
Średnia arytmetyczna: ![]()
Przeciętnie przeczytano około 4,55 książki.
Rozstęp pomiaru: 1 - 9 Osoba, która przeczytała najwięcej książek, przeczytała ich o 8 więcej niż osoba, która przeczytała ich najmniej.
Wariancja: ![]()
Odchylenie standardowe: ![]()
Liczba książek przeczytanych przez poszczególne osoby z próby badanej odchyla się przeciętnie od średniej o 2,46 książki.
Obszar przeciętnej zmienności: xtyp = 4,55 ± 2,46: 2,09 - 7,01 Wyniki typowe dla tej grupy mieszczą się pomiędzy dwoma a siedmioma przeczytanymi książkami.
Współczynnik zmienności: ![]()
Odchylenie standardowe stanowi 54,07% z wartości średniej, a więc - badana grupa jest umiarkowanie zróżnicowana ze względu na liczbę przeczytanych książek.
Współczynnik skośności:
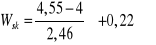
Obserwujemy bardzo słabą skośność dodatnią. W badanej grupie występuje bardzo słaba przewaga mniejszej liczby przeczytanych książek.
Współczynnik asymetrii: ![]()
; ![]()
Występuje słaba skośność dodatnia.
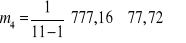
;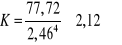
K' = 2,12 - 3 = -0,88
Rozkład danych ma kształt bardziej spłaszczony.
Przykład nr 5
xi |
ni |
ncum |
xi.ni |
(xi -x)2 .ni |
(xi -x)3 .ni |
(xi -x)4 .ni |
1 |
7 |
7 |
7 |
10,59 |
-13,03 |
16,02 |
2 |
7 |
14 |
14 |
0,37 |
-0,09 |
0,02 |
3 |
5 |
19 |
15 |
2,96 |
2,28 |
1,76 |
4 |
2 |
21 |
8 |
6,27 |
11,09 |
19,63 |
5 |
1 |
22 |
5 |
7,67 |
21,25 |
58,87 |
|
22 |
|
49 |
27,86 |
21,52 |
96,30 |
Grupę 22 osób zapytano o liczbę deszczowych dni (xi) podczas tygodniowego pobytu w górach.
Polecenia:
Określić rodzaj danych i skalę pomiarową cechy.
Wyznaczyć i zinterpretować wskaźniki położenia.
Wyznaczyć i zinterpretować wskaźniki rozproszenia.
Wyznaczyć i zinterpretować wskaźniki asymetrii.
Wyznaczyć i zinterpretować wskaźniki skupienia i koncentracji.
Odpowiedzi:
Dane pogrupowane w szereg rozdzielczy punktowy. Skokowa cecha ilościowa, wyrażona na skali stosunkowej.
Dominanta nie występuje - żadnej wartości cechy nie można uznać za typową.
Pozycja mediany: ![]()
albo ![]()
Mediana: Me = 2 Połowa grupy przeżyła do dwóch dni deszczowych i połowa - 2 lub więcej.
Średnia arytmetyczna: ![]()
Przeciętnie zaobserwowano 2,23 dni deszczowych w tygodniu.
Rozstęp mierzonej cechy: 1 - 5 Zaobserwowano od jednego do pięciu dni deszczowych.
Wariancja: ![]()
Odchylenie standardowe: ![]()
Liczba dni deszczowych odchylała się przeciętnie od średniej o 1,15 dnia.
Obszar przeciętnej zmienności: xtyp = 2,23 ± 1,15: 1,08 - 3,38
W zaokrągleniu typowa dla badanej grupy liczba dni deszczowych mieściła się w przedziale od 1 do 3.
Współczynnik zmienności: ![]()
Współczynnik zmienności wskazuje na umiarkowane zróżnicowanie ze względu na liczbę deszczowych dni.
Współczynnika skośności nie można wyznaczyć.
Współczynnik asymetrii: ![]()
![]()
Bardzo słaba skośność dodatnia, czyli bardzo słaba przewaga mniejszej liczby dni deszczowych.
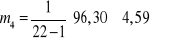
;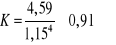
K' = 0,91 - 3 = -2,09
Rozkład danych jest spłaszczony.
Przykład nr 6
xi |
ni |
|
ncum |
|
|
|
|
1 - 3 |
6 |
2 |
6 |
12 |
28,78 |
-63,02 |
138,02 |
3 - 5 |
19 |
4 |
25 |
76 |
0,69 |
-0,13 |
0,02 |
5 - 7 |
4 |
6 |
29 |
24 |
13,10 |
23,72 |
42,93 |
7 - 9 |
1 |
8 |
30 |
8 |
14,52 |
55,31 |
210,72 |
9 - 11 |
1 |
10 |
31 |
10 |
33,76 |
196,12 |
1139,47 |
|
31 |
|
|
130 |
90,84 |
212,00 |
1531,16 |
Grupę 31 osób zapytano o kwotę w zł wydaną na gazety.
Polecenia:
Określić rodzaj danych i skalę pomiarową cechy.
Wyznaczyć i zinterpretować wskaźniki położenia.
Wyznaczyć i zinterpretować wskaźniki rozproszenia.
Wyznaczyć i zinterpretować wskaźniki asymetrii.
Wyznaczyć i zinterpretować wskaźniki skupienia i koncentracji.
Odpowiedzi:
Dane pogrupowane w szereg rozdzielczy klasowy. Cecha ilościowa w przybliżeniu ciągła, wyrażona na skali stosunkowej.
Dominanta:
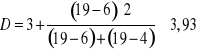
Typowy wydatek na gazety to około 3,93 zł.
Pozycja mediany: ![]()
Mediana: ![]()
Połowa grupy wydaje na gazety co najwyżej 4,05 zł, a połowa - co najmniej 4,05 zł.
Średnia arytmetyczna: ![]()
Przeciętnie wydawano 4,19 zł.
Wariancja:
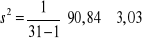
Odchylenie standardowe: ![]()
Kwota wydawana przez poszczególne osoby odchyla się przeciętnie o 1,74 zł w dół lub w górę od średniej.
Obszar przeciętnej zmienności: xtyp = 4,19 ± 1,74: 2,45 - 5,93 Obszar typowych wydatków dla grupy zawarty jest pomiędzy 2,45 a 5,93 zł.
Współczynnik zmienności: ![]()
Współczynnik zmienności wskazuje na umiarkowane zróżnicowanie wydatków na gazety.
Współczynnik skośności:
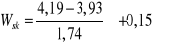
Obserwujemy słabą skośność dodatnią.
Współczynnik asymetrii: ![]()
![]()
Dość silna skośność dodatnia. W badanej grupie występuje wyraźna przewaga mniejszych kwot wydawanych na gazety.
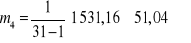
;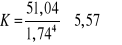
K' = 5,57 - 3 = 2,57
Rozkład danych jest wysmukły.
Wyszukiwarka