Transformata „Z”

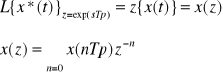
X(t)	X(s)	X(z)
kδ(t)	k	K
1(t)	1/s	z/z-1
t1(t)	1/s^2	zTp/(z-1)^2
t^2/2 1(t)	1/s^3	z(z+1)Tp^2/(z-1)^2
exp(-αt)1(t)	1/(s+α)	z/(z-exp(-αTp))
t exp(-αt)1(t)	1/(s+α)^2	z Tp exp(-αTp)/[z-exp(-αTp)]^2
sin (βt)1(t)	β / s^2 + β^2	z sin(βTp) / z^2-2zcos(βTp)+1
cos (βt)1(t)	s / s^2 + β^2	z [z -cos(βTp)] / z^2-2zcos(βTp)+1

Własności transformaty „Z”

y(t)=bx(t)	x{zb^(-Tp)}
y(t)=tx(t)	-z Tp d/dz{x(z)}
y(t)=x(t-mTp)	z^-mx(z)+z^-m∑x(-kTp)z^k
Y(t)=x(t-mTp)1(t-mTp)	z^-mx(z)
y(t)=x(t+mTp)	z^-mx(z)-z^-m∑x(kTp)z^-k

Modele sygnałowe napięć i prądów:

X(t)=x₁cos(ω₁t+ϕ₁)+x₀exp(-t/Ta)+
∑^l_k=1x_kcos(kω₁t+ϕ_k)+
∑^l_k=1x_0kexp(-t/T_ak)cos(ω_kt+ϕ_k)+e(t),

X(nT_p)=x₁cos(Ω₁+ϕ₁)+x₀exp(-nT_p/Ta)+
∑^l_k=1x_kcos(kΩ₁+ϕ_k)+
∑^l_k=1x_0kexp(-nT_p/T_ak)cos(Ω_k+ϕ_k)+e(nT_p),

gdzie x­₁amplituda składowej podstawowej o częstotliwości 50 Hz, x_k amplitudy składowych harmonicznych o częstotliwościach będących całkowita wielokrotnością 50 Hz, x₀ - amplituda składowej nieokresowej zanikającej ze stała czasowa t_a, x₀ - amplitudy składowych oscylacyjnych zanikających wykładniczo, e(t) - pozostałe składowe sygnału nie uwzględnione w modelu - sygnał błędu.

Twierdzenie o próbkowaniu:

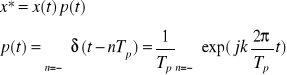
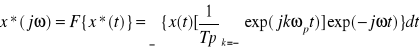
- widmo sygnału próbkowanego

x* - sygnał próbkowany

p(t) - funkcja próbkujaca (wartość funkcji w tym położeniu)

x*(jω0 - widmo sygnału (szereg Fouriera)

p(t) =1/T_p - funkcja próbkujaca jako szereg Fouriera całka wewnętrzna (transf. Fouriera)

1/T­p­ - czynnik próbkujący

- widmo periodyczne takie samo dla ω, ω+2T_p, ω+3T_p

- Warunek Shanona:

ω_p≥2ω_m , gdzie ω_m - najwyższa pulsacja składowych obecnych w sygnale.

- sposoby postępowania prowadzące do odtwarzalności sygnału o konkretnym widmie:

a) dobrać pulsację próbkowania taką, aby spełnić warunek Shanona

b) wybrać mniejszą pulsacje próbkowania, ale ograniczyć widmo sygnału za pomocą odpowiednio zaprojektowanego filtru analogowego, który poprzedza układ próbkowania. W wyniku tego warunek Schanona jest spełniony bez zmiany pulsacji próbkowania.

3.podać transmitancje i równania różnicowe filtów NOI i SOI

Typowy algorytm filtrów NOI (rekursywnych) ma postać:

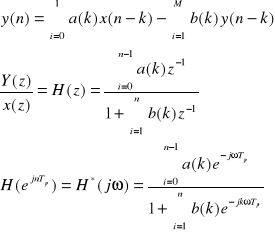
Filtr SOI (nierekursywny)

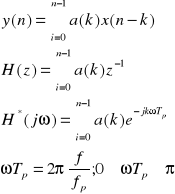
y(n)-n-ta próbka syg. Wyj.

X(n) n-ta próbka syg.wej

A(k),b(k) stałe współ.

Filtr taki wytwarza kolejną próbkę syg.wyj. jak sumę ważoną N poprzednich próbek sygnału oraz M poprzednich próbek syg.wyj.

Filtr nierekursywny tworzy próbkę syg.wyj. wyłącznie z próbek syg.wej.

Filtry parzyste i nieparzyste

4.Warunki uzyskania fitrów o liniowej fazie to odpowiednie parzyste(symetryczne) lub nieparzyste(asymetryczne)

symetrie współ.filtru opisane równaniem

a(k)=a(N-1-K) a(k)=-a(N-1-K)

Można wykazać, że pary filtrów z których jeden spełnia pierwszy z warunków tj. parzystość odpo.impulsowej a drugi nieparzysta odp.impul..Każdy z nich ma liniową fazę w funkcji częstotliwości a różnica ich faz jest równa pi/2 dla dowolnej częstotliwości

Transmitancja widmowa jest określona równaniem:

(1.1)

Można ją wykorzystać do wykazania liniowości fazy i ortogonalności fitrów , których współ. Spełniają podane wyżej warunki symetrii

Uzyskuje się wówczas

(1.2),(1.3)

Znak plus w nawiasie kwadratowym sumy występuje w przypadku parzystej symetrii współ. Filtru , a znak minus w przypadku nieparzystej symetrii.

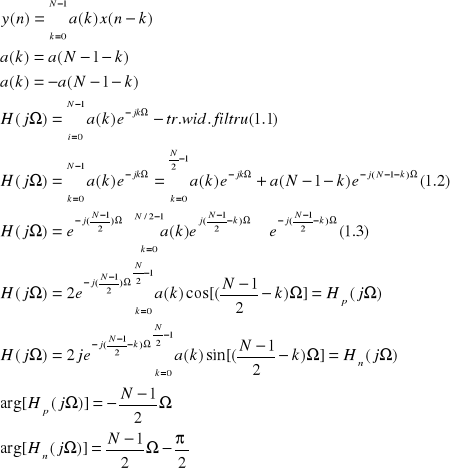
Jeśli współ. Pary filtrów spełniają warunki symetrii parzystej i nieparzystej to oba te filtry mają liniową fazę i są ortogonalne, czyli różnica ich argumentów wynosi pi/2

Filtry Walsha:

Filtr zerowego rzędu:

widmo tego filtru :

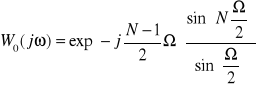
Ω=ωT_p=2πf/f_p

żeby policzyć liczbe próbek albo f_p

Nf/f_p = k i k=1,2,3...

Filtr I rzędu:

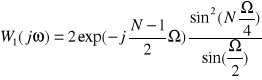
Filtr II rzędu:

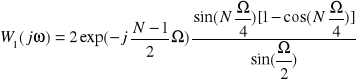
Moduły filtrów pełnookresowych:

|W₁(jΩ₁)|=|W₂(jΩ₁)|=2/(sin(π/N₁)

argumenty:

arg[W₁(jΩ₁)]=π/2-[(N₁-1)/2Ω₁]= -π/2+π/N₁

arg[W₂(jΩ₁)]=-[(N₁-1)/2Ω₁]= -π+π/N₁

Moduły filtrów półokresowych:

|W₀(jΩ₁)|=|W₁(jΩ₁)|=1/(sin(π/N₁)

argumenty:

arg[W₁(jΩ₁)]=π/2-[(N₁/2-1)/2Ω₁]= π/N₁

arg[W₂(jΩ₁)]=-[(N₁/2-1)/2Ω₁]= -π/2+π/N₁

gdzie Ω₁=ω₁/f_p=2π/N₁ N₁=f_p/f₁

Filtry Sin i Cos

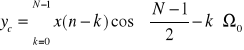
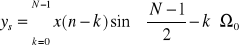
widma:

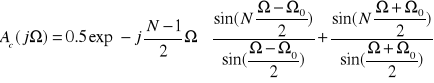
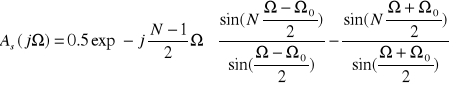
Pomiar składowych impedancji metodami uśredniania

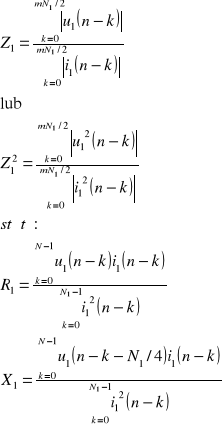
Pomiar częstotliwości przez zliczanie impulsów

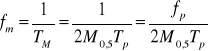
a błąd:

Pomiar częstotliwości i jej odchyleń impulsów zastosowaniem składowych ortogonalnych

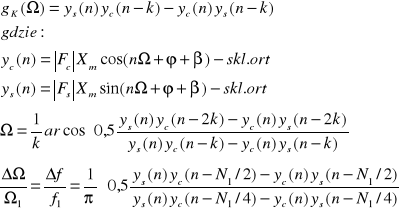
Pomiar napięcia i prądu z wyk. składowych ortogonalnych

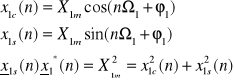
stąd najprostszy algorytm:

a z kolei stąd mamy dwa algorytmy pomiarowe amplitudy prądu i napiecia:

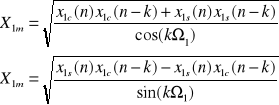
Składowe symetryczne:

[X₀₁₂]=[S][X_ABC], [X₀₁₂]=[x₀,x₁,x₂]

[X_ABC]=[x_a,x_B,x_c]^T

[x]=[x^C]+j[x^S]

a=exp(j2π/3)=-0.5+j√3/2

a²=exp(j4π/3)=-0.5-j√3/2

Po wstawieniu a do macierzy S otrzymujemy dwie macierze: [S]=[S_R]+j[S_I]

[x^C₀₁₂]+j[x^S₀₁₂]={ [S_R]+j[S_I]}{ [x^C_ABC]+j[x^S_ABC]

[x^C₀₁₂]=[S_R] [x^C_ABC]- [S_I] [x^S_ABC]

[x^S₀₁₂]=[S_R] [x^S_ABC]- [S_I] [x^C_ABC]

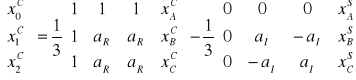
x₀(n)=1/3[x_A(n)+x_B(n)+x_C(n)]

x₁(n)=1/3[x_A(n)+x_B(n-2N₁/3)+x_C(n-N₁/3)]

x₀(n)=1/3[x_A(n)+x_B(n-N₁/3)+x_C(n-2N₁/3)]

Pomiar impedancji pętli zwarciowej dla obw. RL

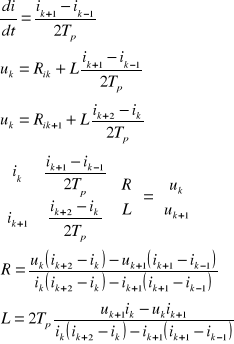
Zad.1 T=10^-3s

T

T

Zad. 4

Dzielimy przez najwyższą potęgę:

__________________________________________

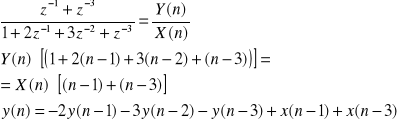
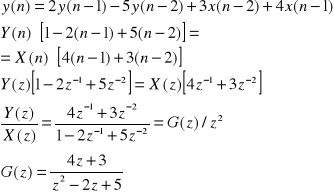
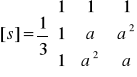
ω_p

G_b

G_a

ω_p

---