POLITECHNIKA LUBELSKA W LUBLINIE		LABORATORIUM ELEKTRONICZNE
				Ćwiczenie nr 4.
OPRUS KURYŚ POGORZELSKI	KRZYSZTOF MICHAŁ WOJCIECH	SEMESTR II	GRUPA 2	ROK AKADEM. 1999/2000
TEMAT ĆWICZENIA: Obwody nieliniowe prądu stałego.			Data wykonania: 14. Marca 2000	OCENA: ..................................

Cel ćwiczenia:

Zapoznanie się z metodami wyznaczania charakterystyk elementów nieliniowych oraz badanie obwodów nieliniowych złożonych z szeregowo i równolegle połączonych elementów nieliniowych metodami graficznymi

1. Wyznaczanie charakterystyki elementów nieliniowych.

Lp.	Element 1		Element 2		Połączenia dwóch nieliniowych elementów:
										Szeregowe 1+2		Równoległe 1+2
		U	I	U	I	U	I	U	I
		V	A	V	A	V	A	V	A
1	2,5	0,52	2,5	0,74	2,5	0,3	2,5	1,26
2	5	0,68	5	1	5	0,55	5	1,68
3	7,5	0,84	7,5	1,24	7,5	0,7	7,5	2,08
4	10	1	10	1,44	10	0,85	10	2,44
5	12,5	1,12	12,5	1,6	12,5	0,9	12,5	2,72
6	15	1,2	15	1,76	15	1	15	2,96
7	17,5	1,32	17,5	1,9	17,5	1,1	17,5	3,22
8	20	1,4	20	2,08	20	1,15	20	3,48
9	22,5	1,5	22,5	2,2	22,5	1,2	22,5	3,7
10	23,8	1,54	23,8	2,28	23,8	1,25	23,8	3,82

Układ do pomiaru charakterystyki pojedynczego elementu nieliniowego:

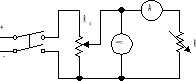
2. Pomiar charakterystyki połączenia szeregowego dwóch elementów nieliniowych.

Lp.	U	I		METODA	I	U1	U2
		V			A			A	V	V
1	1	0,35			a	1,1	12	5
2	6	0,68			b	1,1	11,5	5,5
3	12,4	0,9			c	1,1	12	5
4	17 23,8	1,1
5	23,8	1,32

Metoda:

1. Na podstawie wykresu charakterystyki łącznej i charakterystyki poszczególnych elementów;

2. Na podstawie pomiaru;

3. Na podstawie wykresu, metody przecięcia charakterystyk.

Układ pomiarowy dla połączenia szeregowego:

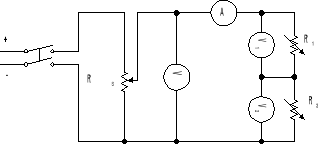
3. Pomiar charakterystyki połączenia równoległego dwóch elementów nieliniowych.

Lp.	I	U		METODA	U	I1	I2
		A			V			V	A	A
1	1,26	2,5			a	10	1	1,44
2	1,7	5			b	10	1	1,43
3	2,43	10			c	10	1	1,44
4	3,21	17,5
5	3,8	23,8

Metoda:

1. Na podstawie wykresu charakterystyki łącznej i charakterystyki poszczególnych elementów;

2. Na podstawie pomiaru;

3. Na podstawie wykresu, metody przecięcia charakterystyk.

Układ pomiarowy dla połączenia równoległego:

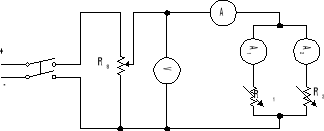
4. Rezystancja statyczna i dynamiczna.

Zakres zmienności rezystancji statycznej i dynamicznej na podstawie wykonanych pomiarów.

statyczna: dla elementu 1 do 15,6 Ω dynamiczna: dla elementu 1do 43,3 Ω

dla elementu 2 do 10,4 Ω dla elementu 2 do 21,6 Ω

5. Aproksymacja charakterystyk doświadczalnych.

Funkcja aproksymująca o postaci I = b · U^d

Lp.	U	Log U		I	Log I
		V	---		A	---
ELEMENT 1
1	5	0,699		0,68	-0,167
2	10	1		1	0
3	15	1,176		1,2	0,079
4	20	1,301		1,4	0,146
5	22,5	1,352		1,5	0,176
ELEMENT 2
1	5		0,699	1	0
2	10	1		1,44	0,158
3	15	1,176		1,76	0,245
4	20	1,301		2,08	0,318
5	22,5	1,352		2,2	0,342

Funkcja aproksymująca dla elementu 1: I₁ = 0,346 · U^0,42

Funkcja aproksymująca dla elementu 2: I₂ = 0,433 · U^0,52

WNIOSKI:

W obwodach elektrycznych często występują elementy nieliniowe, których rezystancja zależy od przepływającego przez nią prądu. Przy dużych prądach następuje nagrzewanie się przewodnika, co w ostateczności prowadzi do zmiany jego rezystancji. Do elementów rezystancyjnych nieliniowych zaliczamy: termistory, baretery, lampy łukowe, prostowniki lampowe i półprzewodnikowe, żarówki z włóknem wolframowym, rezystory wilitowe lub tyrytowe. Przy obliczaniu obwodów nieliniowych korzysta się niekiedy z aproksymacji liniowej (przedziałami) charakterystyki napięciowo-prądowej elementu nieliniowego. Aproksymacja polega na zastąpieniu rzeczywistej charakterystyki odcinkiem prostej w tym zakresie, w którym przebieg charakterystyki rzeczywistej jest zbliżony do linii prostej.

Przy obliczaniu obwodów nieliniowych nie jest spełniona zasada superpozycji, pozostają jednak słuszne prawo Ohma oraz prawa Kirchhoffa. Niemniej jednak metody analityczne zastosowane do obwodów liniowych nie mogą być stosowane w obwodach nieliniowych. Z tego powodu stosuje się metody graficzne od rozwiązywania takich obwodów. Stosuje się dwie metody graficzne: metoda charakterystyk łącznych polegająca na sumowaniu graficznym przebiegów elementów nieliniowych, i metoda przecięcia charakterystyk.

W ćwiczeniu jako elementy nieliniowe zostały wykorzystane żarówki z włóknem wolframowym.

W połączeniu szeregowym dwóch elementów nieliniowych wykorzystaliśmy metodę charakterystyki łączonej sumując napięcia odkładające się na poszczególnych elementach, a także metodę przecięcia się charakterystyk, gdzie spadki napięć przecinają się wyznaczając w ten sposób napięcia na danych elementach przy określonym prądzie.

W połączeniu równoległym przy wyznaczaniu charakterystyk zostały użyte prądy przepływające przez elementy nieliniowe przy stałym określonym napięciu.

Dla pełnego opisania obwodów z elementami nieliniowymi wprowadza się pojęcia aproksymacji charakterystyki elementu nieliniowego tzn.: przedstawienie charakterystyki w postaci wzoru matematycznego, rezystancję dynamiczną i statyczną.

Rezystancja statyczna elementu nieliniowego jest to iloraz napięcia u przez prąd i w danym punkcie charakterystyki. Rezystancja dynamiczna elementu nieliniowego w danym punkcie jest to pochodna napięcia względem prądu w rozpatrywanym punkcie.

Mając wyznaczone doświadczalnie charakterystyki elementów można wyznaczyć charakterystyki połączeń tych elementów. W przypadku połączenia szeregowego przez elementy płynie jednakowy prąd. Napięcia na poszczególnych elementach można wyznaczyć metodą charakterystyki łączonej U = U₁ + U₂, odczytując napięcie w punktach, w których prosta równoległa do osi rzędnych i przechodząca przez punkt odpowiadający zadanemu prądowi I przecina wykresy. Jeżeli znamy napięcia na zaciskach możemy wyznaczyć prąd płynący w obwodzie i napięcia na poszczególnych elementach metodą przecięcia charakterystyk. Rysując charakterystykę elementu 1 I(U) w układzie współrzędnych, a następnie odkładając na osi odciętych punkt P odpowiadający napięciu na zaciskach rysujemy charakterystykę drugiego elementu symetrycznie względem osi I' przechodzącej przez punkt P. punkt przecięcia charakterystyk wyznacz nam wartość prądu płynącego w obwodzie i napięcia na poszczególnych elementach. Analogicznie wyznaczamy rozpływ prądu w gałęziach równoległych obwodów nieliniowych. Napięcie na elementach jest jednakowe, a prąd ulega rozgałęzieniu I = I₁ + I₂. Mając dane napięcie możemy wyznaczyć z charakterystyki łączonej prąd w poszczególnych gałęziach obwodu. Gdy dany jest prąd I dopływający do połączenia, metodą przecięcia charakterystyk można wyznaczyć napięcie na zaciskach i prądy w poszczególnych gałęziach.

Charakterystyki wyznaczone na drodze pomiarowej w sposób graficzny można przedstawić analitycznie w postaci równania określającego zależność I(U). Aproksymacja pozwala rozwiązywać układy z elementami nieliniowymi metodami analitycznymi.

---