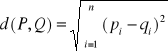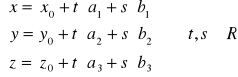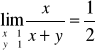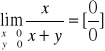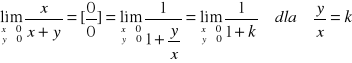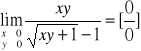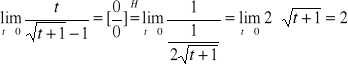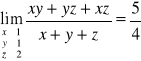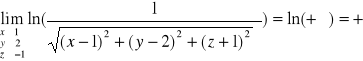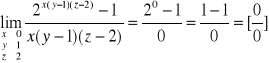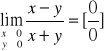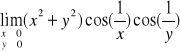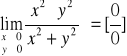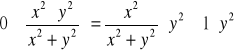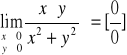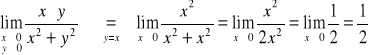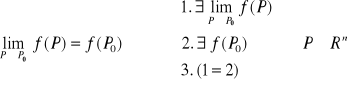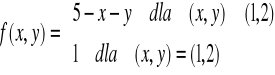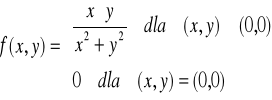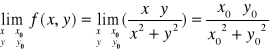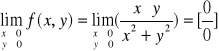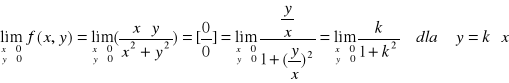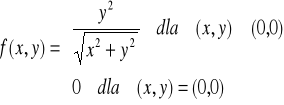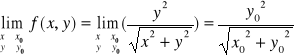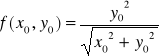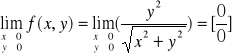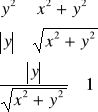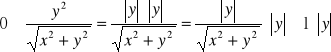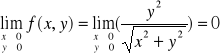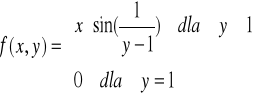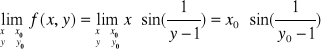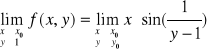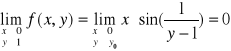AM2:WYKŁAD-1

METRYKA I TOPOLOGIA PRZESTRZENI R^n DZIEDZINA FUNKCJI WIELU ZMIENNYCH GRANICA FUNKCJI WIELU ZMIENNYCH CIĄGŁOŚĆ FUNKCJI WIELU ZMIENNYCH

Rozważając funkcje rzeczywiste jednej zmiennej rzeczywistej mieliśmy do czynienia z dziedziną funkcji Dom(f) i zbiorem wartości Im(f).

Zbiory te były podzbiorami zbioru liczb rzeczywistych R.

Dla funkcji wielu zmiennych rzeczywistych o wartościach rzeczywistych

o których będziemy mówić na tym wykładzie dziedziną będzie iloczyn kartezjański zbioru R a zatem ogólnie sytuacja wygląda nieco inaczej:

Ażeby nasze rozważania były ogólne wprowadzimy też ogólne pojęcie odległości (metryki) w zbiorze A.

Odległością d miedzy elementami P oraz Q zbioru A będziemy nazywali funkcję która przekształca iloczyn kartezjański AxA w zbiór liczb nieujemnych i ma określone własności: nieujemność symetria warunek trójkąta dla elementów P,Q,R Jeżeli nie jest spełniony warunek 4. to funkcję d nazywamy półodległością Parę (A,d) nazywamy: przestrzenią metryczną jeżeli spełnione są warunki 1,2,3,4 przestrzenią półmetryczną jeżeli są spełnione warunki 1,2,3

W szczególności w zbiorze którego elementami sa punkty oraz możemy wprowadzić odległość kartezjańską określoną definicją:

Przykładowo:

w zbiorze

w zbiorze

w zbiorze

Wprowadzimy też pojęcie otoczenia
punktu
o promieniu

oraz sąsiedztwa
punktu
o promieniu
.

Zdefiniujemy teraz pojęcia charakterystycznych punktów zbioru.

Punkt wewnętrzny zbioru A Punkt jest punktem wewnętrznym zbioru A czyli jeżeli istnieje otoczenie tego punktu całkowicie zawarte w zbiorze A

Punkt zewnętrzny zbioru A Punkt jest punktem zewnętrznym zbioru A czyli jeżeli istnieje otoczenie tego punktu które nie zawiera żadnego punktu ze zbioru A

Punkt brzegowy zbioru A Punkt jest punktem brzegowym zbioru A czyli w każdym otoczeniu tego punktu są punkty należące do zbioru A i są punkty nie należące do zbioru A.

Punkt skupienia zbioru A Punkt jest punktem skupienia zbioru A czyli jeżeli w każdym sąsiedztwie tego punktu możemy znależć punkty ze zbioru A Przykładowo: punkty wewnętrzne i punkty brzegowe są punktami skupienia zbioru.

Lokalizacja punktu wewnętrznego Pw, brzegowego Pb i zewnętrznego Pz.

Przy pomocy tych pojęć określimy nowe ważne definicje:

• Zbiór ograniczony

• Zbiór otwarty

• Zbiór domknięty

• Zbiór spójny (obszar)

Zbiór A jest ograniczony

Zbiór A jest otwarty zawiera wyłącznie punkty wewnętrzne

Zbiór A jest domknięty zawiera wyłącznie punkty skupienia (wewnętrzne i brzegowe)

Zbiór A jest obszarem Jest zbiorem otwartym Każde dwa punkty można połączyć łamaną całkowicie zawartą w tym zbiorze

Można też wypisać kilka wniosków wynikających z powyższych definicji.

Przestrzeń R^n oraz zbiór ∅ jest jednocześnie zbiorem otwartym i domkniętym

Dopełnienie zbioru otwartego jest zbiorem domkniętym

Dopełnienie zbioru domkniętego jest zbiorem otwartym

Żaden punkt brzegowy zbioru otwartego do niego nie należy

Każdy punkt brzegowy zbioru domkniętego do niego należy

Wprowadzimy teraz ważne pojęcie topologii przestrzeni metrycznej.

Topologią przestrzeni metrycznej (A,d) nazywamy rodzinę indeksowaną podzbiorów otwartych zbioru A takich że zachodzą nastepujące własności: jest zbiorem otwartym zawartym w jest zbiorem otwartym zawartym w jest zbiorem otwartym zawartym w jest zbiorem otwartym zawartym w

Można wykazac że każda przestrzeń metryczna jest przestrzenią topologiczną.

Przejdźmy teraz do definicji funkcji wielu zmiennych

Funkcją n-zmiennych rzeczywistych nazywamy przyporządkowanie każdemu punktowi P zbioru dokładnie jednej liczby rzeczywistej Zbiór D nazywamy dziedziną funkcji wielu zmiennych. Zbiór punktów P przestrzeni dla których wzór funkcji f(P) ma sens nazywamy dziedziną naturalną

Przykład funkcji 2-zmiennych:

Przykład funkcji 3-zmiennych:

Wykresem funkcji 2- zmiennych nazywamy zbiór Wykresem funkcji 2-zmiennych jest zazwyczaj powierzchnia w przestrzeni Poziomicą wykresu funkcji 2-zmiennych odpowiadajacą poziomowi z=h nazywamy zbiór Poziomice powstają poprzez przecięcie wykresu funkcji płaszczyznami z = const. Powstałe krzywe rzutujemy na płaszczyznę XY tworząc plan warstwicowy. Plan warstwicowy funkcji 2-zmiennych - zbiór poziomic dla różnych poziomów.

Wykresem funkcji 3- zmiennych nazywamy zbiór

Rozpatrzmy teraz podstawowe powierzchnie w przestrzeni
, które są wykresami odpowiednich funkcji dwóch zmiennych.

Płaszczyzna: Równanie ogólne płaszczyzny: Wektor [A,B,C] jest prostopadły do płaszczyzny Równanie odcinkowe płaszczyzny: Stałe a,b,c oznaczają miary punktów w których płaszczyzna przecina osie OX,OY,OZ Równanie parametryczne płaszczyzny przechodzącej przez punkt i generowanej przez wektory

Sfera: Równanie sfery o środku w punkcie i promieniu R:

Paraboloida obrotowa: Równanie paraboloidy obrotowej o osi z:

Stożek: Równanie stozka o osi z i kącie rozwarcia :

Walec: Fragment walca nieskończonego o osi z i promieniu r :

Zanim przejdziemy do sformułowania granicy funkcji wielu zmiennych w punkcie wykorzystamy naszą metrykę do określenia co oznacza zbieżność punktów.

Ciąg punktów dąży do punktu ciąg odległości dąży do zera Zapisujemy to krótko:

W przestrzeni Warunek Czyli mamy jednoczesną zbieżność dwóch współrzędnych punktów

W przestrzeni Warunek Czyli mamy jednoczesną zbieżność trzech współrzędnych punktów

Teraz już możemy sformułować definicję granicy funkcji w punkcie.

Warto zwrócić uwage na to że dla każdego zbieżnego ciągu punktów ciąg wartości funkcji musi być zbieżny do tej samej granicy g - funkcja nie może mieć dwóch różnych granic. Jeżeli dla dwóch różnych ciągów argumentów wartości graniczne są różne to funkcja nie ma granicy w tym punkcie.

PRZYKŁADY GRANIC FUNKCJI 2-ZMIENNYCH Przykład-1 granicy funkcji 2-zmiennych Po wstawieniu wartości granicznych x i y otrzymujemy wyrażenie oznaczone ½ i to jest granicą naszej funkcji dwóch zmienych w punkcie (1,1). Przykład-2 granicy funkcji 2-zmiennych W tym przypadku otrzymujemy wyrazenie nieoznaczone typu 0/0 i jak pamiętamy z funkcji jednej zmiennej jest to sygnał do przekształcenia tego wyrażenia w celu usunięcia tej nieoznaczoności. Jednym ze sposobów jest podzielenie licznika i mianownika przez x. Teraz należy tylko zauważyć że jeżeli będziemy zbliżać się do punktu (0,0) wzdłuż prostych y=kx o różnych nachyleniach k to dostaniemy różne wartości graniczne np. dla k=1 wartośc graniczna =1/2 a dla k=2 wartośc graniczna = 1/3 co jest niezgodne z definicją granicy funkcji w punkcie (0,0) . W poprzednim przykładzie dostaliśmy wyrażenie nioznaczone typu 0/0 co w analogii do funkcji jednej zmiennej sugeruje że oprócz przekształcenia algebraicznego moglibyśmy zastosować regułę de L'Hospitala. Jednakże wtedy nasuwa się pytanie po jakim argumencie mamy różniczkować licznik i mianownik ? Po argumencie x czy po argumencie y ? Otóż dla funkcji 2,3 i wiecej zmiennych nie ma zastosowania reguła de L'Hospitala chyba że uda nam się wprowadzić nową zmienną i dla tej nowej zmiennej zastosujemy tę regułę. Przykład-3 granicy funkcji 2-zmiennych W tym przypadku dostaliśmy wyrazenie nieoznaczone typu 0/0 i oczywiście możemy dokonać przekształcenia algebraicznego ale zastosujmy teraz metodę wprowadzenia nowej zmiennej t = xy. Zauważmy że a zatem nasza granica jest granicą funkcji jednej zmiennej t i do niej stosujemy regułę de L'Hospitala funkcji jednej zmiennej. .

PRZYKŁADY GRANIC FUNKCJI 3-ZMIENNYCH Przykład-1 granicy funkcji 3-zmiennych Tutaj też mamy wyrażenie oznaczone i to jest granica funkcji 3-zmiennych Przykład-2 granicy funkcji 3-zmiennych Przykład-3 granicy funkcji 3-zmiennych Otrzymujemy wyrażenie nieoznaczone typu 0/0 i wprowadzamy nową zmienną t = x(y-1)(z-2) i mamy granicę funkcji jednej zmiennej t :

Dla funkcji 2-zmiennych wprowadzimy teraz pożyteczne pojęcie granic iterowanych.

Liczbę g dla funkcji 2-zmiennych nazywamy granicą lub granicą podwójną w odróżnieniu od tak zwanych granic iterowanych funkcji 2-zmiennych.

Granice iterowane funkcji f(x,y) definiujemy następująco: Podstawowa różnica między granicą podwójną a granicami iterowanymi jest jednoczesność i odpowiednio sekwencyjność wykonywania operacji granicznych. W granicy podwójnej przejscie graniczne wykonujemy jednocześnie dla x i dla y a w granicach iterowanych sekwencyjnie (kolejno) dla każdej zmiennej osobno. W granicy iterowanej g1 najpierw wykonujemy przejscie graniczne dla y przy ustalonym x (granica wewnętrzna) a w następnej kolejności przejście graniczne dla x (granica zewnętrzna). W granicy iterowanej g2 najpierw wykonujemy przejscie graniczne dla x przy ustalonym y (granica wewnętrzna)a w następnej kolejności przejście graniczne dla y (granica zewnętrzna). Widać zatem że granice iterowane liczymy jak kolejne granice funkcji jednej zmiennej (druga zmienna jest ustalona)

Naturalnym wydaje się pytanie o związek granicy podwójnej z granicami iterowanymi. Jest on generalnie bardzo luźny - może istnieć granica podwójna g a nie istnieją granice iterowane g1 i g2 oraz mogą istnieć granice iterowane a nie istnieć granica podwójna. W praktyce przydatne sa następujące trzy implikacje: Obliczenie granic iterowanych pozwala postawić hipotezę jaka liczba może być granicą podwójną funkcji ale istnienie granic iterowanych (właściwych) nie przesądza o istnieniu granicy podwójnej (należy pamietać że są to implikacje). Na podstawie trzeciej implikacji można powiedzieć tylko tyle że jeżeli granice iterowane właściwe istnieją i są różne to nie istnieje granica podwójna

PRZYKŁADY WYKORZYSTYWANIA GRANIC ITEROWANYCH DO OBLICZANIA GRANIC PODWÓJNYCH Przykład-1: granice iterowane istnieją, granica podwójna nie istnieje Bezpośrednio licząc granicę podwójną otrzymaliśmy wyrażenie nieoznaczone 0/0. Możemy oczywiście przekształcić ale dla ilustracji spróbujmy obliczyć granice iterowane. A zatem granice iterowane właściwe istnieją ale są różne a więc nie istnieje granica podwójna. Przykład-2: granice iterowane nie istnieją, granica podwójna istnieje Łatwo widzieć że granica podwójna = 0 gdyż funkcja a funkcje są ograniczone zatem z twierdzenia o 3 ciągach iloczyn takich funkcji dąży do 0. Natomiast granice iterowane nie istnieją jak widać po prostych obliczeniach granica wewnętrzna nie istnieje a tym samym nie istnieje granica iterowana granica wewnętrzna nie istnieje a tym samym nie istnieje granica iterowana Przykład-3: granice iterowane istnieją i są równe , granica podwójna istnieje Badamy granice iterowane: A zatem jeżeli istnieje granica podwójna to musi być równa 0. Wykażemy że ta hipoteza jest prawdziwa z twierdzenia o 3 ciagach. ponieważ Ponieważ funkcja z twierdzenia o 3 ciągach wynika że granica podwójna rzeczywiscie wynosi 0 - potwierdziliśmy postawioną poprzednio hipotezę. Przykład-4: granice iterowane istnieją i są równe , granica podwójna nie istnieje Liczymy granice iterowane. a więc znów jeżeli granica podwójna istnieje to musi być równa 0. Ale w tym przypadku szybkość zbieżności do zera licznika i mianownika jest taka sama zatem możemy podejrzewać że dla pewnego ciągu argumentów otrzymamy granicę stałą różną od zera. Przyjmijmy że ciąg argumentów dąży do punktu (0,0) wzdłuż prostej y = x . Wówczas granica podwójna upraszcza się do granicy funkcji jednej zmiennej: a więc widać że dla takiego ciagu punktów wartość graniczna nie jest równa zeru a zatem granica podwójna nie istnieje.

Mając określoną definicję granicy funkcji wielu zmiennych oraz sposoby jej obliczania możemy podać ogólną definicję ciągłości funkcji wielu zmiennych w danym punkcie.

Mówimy że funkcja f(P) jest ciągła w punkcie P0 czyli wtedy gdy granicą funkcji w danym punkcie jest wartość tej funkcji w tym punkcie. Równość ta daje podstawową analityczną interpretację funkcji ciągłej: czyli operator granicy funkcji ciągłej możemy przenosić pod znak funkcji. Równość definicyjna jest równoważna trzem warunkom ciągłości: f(P) ciągla w P0 ⇔

PRZYKŁADY OKREŚLANIA PUNKTÓW CIĄGŁOŚCI I NIECIĄGŁOŚCI FUNKCJI Przykład-1: Zbadać ciągłość funkcji określonej następująco: Definicja funkcji podzieliła dziedzinę funkcji R² na dwa obszary: Obszar-I : zbiór punktów (x,y) ≠ (1,2) Obszar-II: punkt (1,2) Zbadajmy najpierw ciągłość funkcji w dowolnym punkcie (x0,y0) obszaru-I, a tym samym 3 warunki ciągłości funkcji w tym punkcie. Warunek-1: Warunek-2: Warunek-3: Ponieważ wszystkie 3 warunki ciągłości są spełnione wnioskujemy że funkcja jest ciągła w każdym punkcie obszaru-I. A co z ciągłością w obszarze-II ? Składa się on tylko z jednego punku (1,2) zatem badamy ciągłość tylko w tym punkcie. Warunek-1: Warunek-2: Warunek-3: Ponieważ nie spełniony jest warunek-3 ciągłości więc w tym punkcie funkcja nie jest ciągła. Podsumowując funkcja jest ciagła w całej swojej dziedzinie za wyjątkiem punku (1,2) co krótko można zapisać że jest ciągła w zbiorze R²-{(1,2)} Przykład-2: Zbadać ciągłość funkcji określonej następująco: Definicja funkcji podzieliła dziedzinę funkcji R² na dwa obszary: Obszar-I : zbiór punktów (x,y) ≠ (0,0) Obszar-II: punkt (0,0) Zbadajmy najpierw ciągłość funkcji w dowolnym punkcie (x0,y0) obszaru-I, a tym samym 3 warunki ciągłości funkcji w tym punkcie. Warunek-1: Warunek-2: Warunek-3: Ponieważ wszystkie 3 warunki ciągłości są spełnione wnioskujemy że funkcja jest ciągła w każdym punkcie obszaru-I. A co z ciągłością w obszarze-II ? Składa się on tylko z jednego punku zatem badamy ciągłość tylko w tym punkcie. Warunek-1: Mamy zatem wyrażenie nieoznaczone i przekształcamy dzieląc licznik i mianownik przez x² Jeżeli zatem będziemy zbiegali do punktu (0,0) wzdłuż prostych y=kx to dla róznych wartości k dostaniemy różne wartości graniczne np. dla k=1 wartość graniczna=1/2 a dla wartości k=2 wartość graniczna=2/5 czyli w punkcie (0,0) funkcja nie ma granicy. Wprawdzie spełniony jest warunek drugi Warunek-2: ale nie spełniony jest oprócz warunku 2 również warunek 3 Warunek-3: nie można porównać bo granica nie istnieje Zatem funkcja nie jest ciągła w punkcie (0,0) Podsumowując funkcja jest ciagła w całej swojej dziedzinie za wyjątkiem punku (0,0) co krótko można zapisać że jest ciągła w zbiorze R²-{(0,0)} Przykład-3: Zbadać ciągłość funkcji określonej następująco: Definicja funkcji podzieliła dziedzinę funkcji R² na dwa obszary: Obszar-I : zbiór punktów (x,y) ≠ (0,0) Obszar-II: punkt (0,0) Zbadajmy najpierw ciągłość funkcji w dowolnym punkcie (x0,y0) obszaru-I, a tym samym 3 warunki ciągłości funkcji w tym punkcie. Warunek-1: Warunek-2: Warunek-3: Ponieważ wszystkie 3 warunki ciągłości są spełnione wnioskujemy że funkcja jest ciągła w każdym punkcie obszaru-I. A co z ciągłością w obszarze-II ? Składa się on tylko z jednego punku zatem badamy ciągłość tylko w tym punkcie. Warunek-1: Mamy zatem wyrażenie nieoznaczone ale w tym przypadku stopień licznika jest wyższy niż mianownika i granicą może być liczba 0. Ażeby to wykazać stosujemy twierdzenie o 3 ciągach wychodząc z następujacych nierówności: Zatem mamy oszacowanie wartości funkcji od góry i od dołu: ale przecież oba ograniczenia dążą do zera gdyż zatem z twierdzenia o 3 ciagach Warunek-2: Warunek-3: Zatem funkcja jest ciągła w punkcie (0,0) Podsumowując funkcja jest ciagła w całej swojej dziedzinie co krótko można zapisać że jest ciągła w zbiorze R². Przykład-4: Zbadać ciągłość funkcji określonej następująco: Definicja funkcji podzieliła dziedzinę funkcji R² na dwa obszary: Obszar-I : zbiór punktów nie leżących na prostej y = 1 Obszar-II: zbiór punktów leżących na prostej y = 1 Zbadajmy najpierw ciągłość funkcji w dowolnym punkcie (x0,y0) obszaru-I, a tym samym 3 warunki ciągłości funkcji w tym punkcie. Warunek-1: Warunek-2: Warunek-3: Ponieważ wszystkie 3 warunki ciągłości są spełnione wnioskujemy że funkcja jest ciągła w każdym punkcie obszaru-I. A co z ciągłością w obszarze-II ? Tym razem składa się on tylko z nieskończonej ilości punktów położonych na prostej y = 1 zatem musimy rozważyć istnienie granicy dla różnych wartości x. Rozważmy najpierw punkt Warunek-1: Widać że taka granica nie istnieje bo funkcja może przyjmować na przemian wartości 1,0,-1 a wartość . Zatem w tych punktach na prostej y = 1 funkcja nie jest ciągła. Rozważmy jeszcze ostatni punkt na tej prostej tzn. punkt (0,1) i zbadajmy warunki ciągłości w tym punkcie. Warunek-1: Bo nasza funkcja jest iloczynem funkcji dążącej do zera i ograniczonej. Warunek-2: Warunek-3: Zatem funkcja jest ciągła w punkcie (0,1) Podsumowując funkcja jest ciągła w całej swojej dziedzinie za wyjątkiem wszystkich punktów leżących na prostej y = 1 dla których x≠0 co krótko można zapisać że jest ciągła w zbiorze R²-{(x,1): x≠0}

Wymieńmy jeszcze ważne dla zastosowań własności funkcji ciągłych:

Własności elementarne (arytmetyka ciągłości)

1	Suma funkcji ciągłych w punkcie Po jest funkcją ciągłą w punkcie Po
2	Różnica funkcji ciągłych w punkcie Po jest funkcją ciągłą w punkcie Po
3	Iloczyn funkcji ciągłych w punkcie Po jest funkcją ciągłą w punkcie Po
4	Iloraz funkcji ciągłych w punkcie Po jest funkcją ciągłą w punkcie Po , dla którego mianownik ≠0

Własności nieelementarne

1	O lokalnym zachowaniu znaku: { Funkcja f(P) określona w otoczeniu punktu Po ; f(P) ciągła w Po; f(Po) > 0; odpowiednio f(Po) < 0 } { w pewnym otoczeniu Po zachodzi f(P) > 0; odpowiednio f(P) < 0 }
2	O osiąganiu kresów (Weierstrassa): { f(P) ciągła na zbiorze domkniętym i ograniczonym } ⇒ { przyjmuje na tym zbiorze wartość największą (kres górny) i wartość najmniejszą (kres dolny) }
3	O przyjmowaniu wartości pośrednich (Darboux) { f(P) ciągła na zbiorze domkniętym i ograniczonym } ⇒ { przyjmuje na tym zbiorze wszystkie wartości pośrednie pomiedzy kresem górnym i dolnym }
4	O ciągłości jednostajnej: { f(P) ciągła na zbiorze domkniętym i ograniczonym } ⇒ { f(P) ciągła jednostajnie na tym zbiorze }
5	O punkcie stałym { f(P) ciągła na zbiorze domkniętym i ograniczonym D; f: D→D } ⇒ { f(P) ma punkt stały tzn. ∃ Po∈D: f(Po) = Po }

Autor: Wojciech Drabik (PJWSTK)

5

ZADANIE:

Naszkicuj plan warstwicowy paraboloidy obrotowej dla kilku wybranych poziomic.

ROZWIĄZANIE:

Równanie paraboloidy obrotowej ma postać

Widać że wartości funkcji są nieujemne zatem poziomice zaczynamy od 0.

Dla
; rozwiązaniem jest punkt (0,0)

Dla
; Okrąg o środku (0,0) i r = 1

Dla
; okrąg o środku (0,0) i r = 2

A więc już widać że dalsze poziomice też będą okręgami o o środku (0,0) i różnych promieniach.

ZADANIE:

Określ dziedzinę naturalną funkcji

ROZWIĄZANIE:

Wyrażenie ma sens jeżeli
czyli
czyli

Zatem dziedziną naturalną będzie cała płaszczczyzna bez prostych

ZADANIE:

Na podstawie powyższych definicji wykaż ze zbiór

nie jest otwarty ani nie jest domknięty.

ROZWIĄZANIE:

Punkt A(1, 1/2) należy do zbioru ale nie jest punktem wewnętrznym - zbiór nie jest zatem zbiorem otwartym

Punkt B(1,1) jest punktem skupienia naszego zbioru ale nie należy

do tego zbioru - zbiór nie jest zatem zbiorem domkniętym.

---