ZADANIA
Geometria analityczna
Oblicz współrzędne wektora
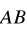
, jeśli:
a) ![]()
, ![]()
; b) ![]()
, ![]()
;
c) ![]()
, ![]()
; d) ![]()
, ![]()
.
Oblicz długość wektora
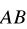
, jeśli:
a) ![]()
, ![]()
; b) ![]()
, ![]()
;
c) ![]()
, ![]()
; d) ![]()
, ![]()
.
Dane są punkty

,
,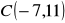
. Punkt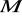
jest środkiem odcinka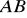
,
a ![]()
- środkiem odcinka ![]()
. Oblicz współrzędne i długości następujących wektorów:

; b)
.
Dane są punkty
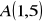
,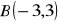
,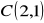
,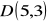
,
,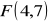
. Wśród wektorów
,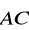
,
,
,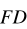
,
wskaż pary wektorów równych i pary wektorów przeciwnych. Które wektory mają tę samą długość?
Dla jakich liczb rzeczywistych

,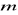
wektory
i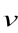
są przeciwne, jeśli: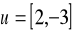
,
; b)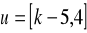
,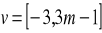
.
Dany jest odcinek o końcach

i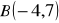
. Wyznacz współrzędne punktu
, który tak dzieli odcinek
, że:
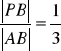
; b)
.
Dane są punkty
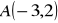
,
,
,
. Oblicz współrzędne wektorów:
a) ![]()
; b) ![]()
.
Dane są punkty
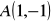
,
,
. Wyznacz taki punkt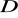
, by
.
Oblicz iloczyn skalarny wektorów:
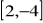
i
; b)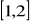
i
; c)
i
.
Wyznacz kąt między wektorami:

i
; b)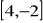
i
; c)
i
.Wyznacz kąty trójkąta

o wierzchołkach: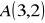
,
,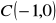
; b)
,
,
.
Wykaż, że przekątne czworokąta

, w którym
,
,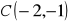
,
są prostopadłe.Dane są wektory:
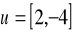
,
. Oblicz: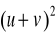
; b)
; c)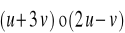
.
Oblicz iloczyn wektorowy podanej pary wektorów:

,
; b)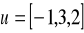
,
.
Obliczyć pole równoległoboku rozpiętego na wektorach:

,
; b)
,
.
Dla jakiej wartości
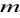
punkty
,
i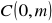
są wierzchołkami trójkąta prostokątnego?
Napisz równanie prostej prostopadłej do wektora

i przechodzącej przez punkt: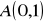
; b)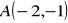
; c)
.
Udowodnij, że proste o równaniach

i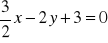
są równoległe.
Udowodnij, że proste o równaniach
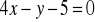
i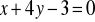
są prostopadłe.
Dane są dwie proste o równaniach

i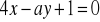
. Dla jakich wartości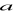
i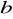
proste te są:równoległe; b) prostopadłe.
Napisz równanie prostej przechodzącej przez punkt
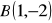
oraz:równoległej do prostej

;prostopadłej do prostej
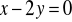
;równoległej do osi

.
Wektor
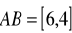
jest podstawą trójkąta równoramiennego o wierzchołku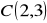
i wektorze wysokości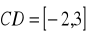
. Znajdź równania prostych zawierających boki tego trójkąta.
Wyznacz równanie postaci
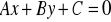
, gdzie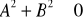
, prostej
.
Wyznacz równanie parametryczne prostej

.
Wykaż, że układy równań
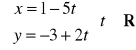
oraz 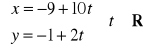
opisują tę samą prostą
Udowodnij, że punkt

należy do prostej
.
Wyznacz współrzędne punktu przecięcia się prostych
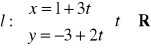
oraz 
.
Wyznacz równania parametryczne prostej przechodzącej przez punkt

oraz:równoległej; b) prostopadłej
do prostej 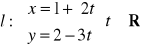
.
Napisz równanie parametryczne prostej:
przechodzącej przez punkt
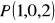
i równoległej do wektora
;przechodzącej przez punkty
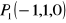
,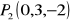
.
Napisz równanie płaszczyzny przechodzącej przez punkt
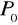
i prostopadłej do wektora
, jeśli:
,
; b)
,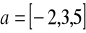
.
Napisz równanie płaszczyzny przechodzącej przez środek odcinka

, gdzie
.
i prostopadłej do tego odcinka.Napisz równania parametryczne płaszczyzny przechodzącej przez środek układu współrzędnych i równoległej do wektorów

,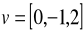
.Napisz równania parametryczne płaszczyzny przechodzącej przez punkt
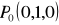
i równoległej do wektorów
,
.Napisz równania ogólne i parametryczne płaszczyzny przechodzącej przez punkty

,
,
Zbadaj czy punkty

,
należą do prostej
.Zbadaj czy punkty

,
należą do płaszczyzny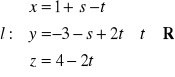
.
Znajdź odległość punktu
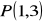
od prostej
o równaniu: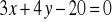
; b)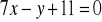
.
Znajdź odległość prostych równoległych

,
.Znajdź odległość
punktu

od płaszczyzny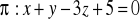
;płaszczyzn równoległych

,
.
Znajdź rzut prostokątny
punktu
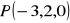
na płaszczyznę
;prostej
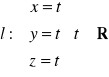
na płaszczyznę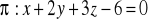
.
Znajdź rzut równoległy punktu

; b)
na płaszczyznę ![]()
w kierunku prostej 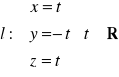
.
Przez punkty

i
leżące poza płaszczyzną
poprowadzono proste prostopadłe do tej płaszczyzny, przebijające ją odpowiednio w punktach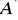
i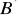
. Wiedząc, że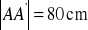
i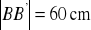
, oblicz odległość środka odcinka
od płaszczyzny
.
Z punktów
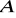
i
płaszczyzny
poprowadzono poza nią dwa równoległe do siebie odcinki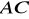
i
,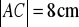
,
. Prosta przechodząca przez punkty
i
przebija płaszczyznę w punkcie
. Wiedząc, że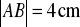
, wyznacz długość
odcinka ![]()
.
Odcinek
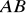
ma długość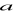
i jest nachylony do płaszczyzny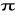
pod kątem: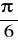
; b)
; c)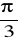
.
Oblicz długość rzutu prostokątnego tego odcinka na płaszczyznę ![]()
.
Jedna z przyprostokątnych trójkąta prostokątnego równoramiennego leży w płaszczyźnie
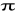
, a druga tworzy z płaszczyzną
kąt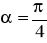
. Jaki kąt tworzy przeciwprostokątna trójkąta z płaszczyzną?
Odległość między dwiema płaszczyznami równoległymi

i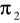
wynosi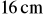
. Końce odcinka długości
leżą na tych płaszczyznach. Oblicz długość rzutu tego odcinka na płaszczyznę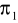
.
Wyznacz współrzędne środka

i długość promienia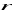
okręgu danego równaniem: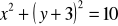
; b)
.
Określ wzajemne położenie prostej
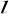
i okręgu
, jeśli:
,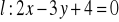
;
,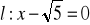
;
,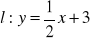
.
Określ wzajemne położenie okręgów:

,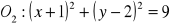
;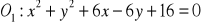
,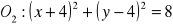
;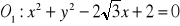
,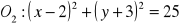
.
Wyznacz współrzędne punktów wspólnych dwóch okręgów opisanych równaniami
![]()
oraz ![]()
.
Znajdź równanie okręgu o środku w punkcie
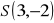
, stycznego do prostej o równaniu
![]()
.
Znajdź równania stycznych do okręgu o równaniu

, przechodzących przez punkt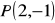
.
Napisz wzór na translację o wektor

, gdy: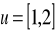
; b)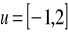
; c)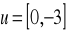
.
Znajdź obrazy punktów:

,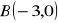
,
w translacji o wektor
.
Dane są punkty

,
,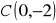
. Napisz wzór opisujący translację o wektor: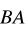
; b)
; c)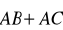
.
Znajdź równanie obrazu prostej o równaniu

w translacji o wektor
.
Znajdź równanie obrazu okręgu o równaniu
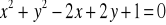
w translacji
o wektor ![]()
.
Znajdź równanie obrazu paraboli o równaniu

w translacji o wektor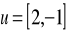
.
Dane są punkty
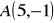
,
,
. Znajdź translację, w której:obrazem punktu

jest punkt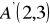
;obrazem środka
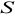
odcinka
jest punkt
.
Dla jakich wartości
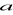
przekształcenie
płaszczyzny określone wzorami:
jest translacją o wektor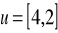
.
Wyznacz translację, w której obrazem linii

jest linia
, gdy: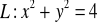
,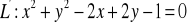
;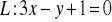
,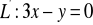
.
Wykaż, że obrazem prostej w translacji jest prosta do niej równoległa.
Znajdź obrazy punktów
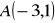
,
,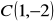
,
w symetrii względem punktu:
; b)
; c)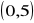
.
Znajdź równanie okręgu, który jest obrazem okręgu o równaniu
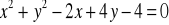
w symetrii względem punktu
, gdy:
; b)
; c)
.
Znajdź równanie obrazu linii

w symetrii względem punktu
, gdy: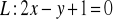
,
,
;
,
,
.
Wyznacz symetrię środkową, w której obrazem punktu

jest punkt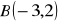
.
Znajdź obrazy punktów
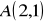
,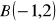
w obrocie dookoła punktu
o kąt
.
Znajdź wierzchołek
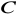
trójkąta równobocznego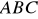
, wiedząc, że
,
.
Znajdź równanie obrazu prostej o równaniu

w obrocie dookoła punktu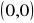
o kąt ![]()
.
Znajdź równanie obrazu okręgu o równaniu
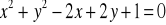
w obrocie dookoła punktu
o kąt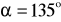
.Znajdź obrazy punktów

,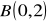
,
w jednokładności o środku
i stosunku
, gdy:
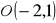
,
; b)
,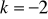
;
c) ![]()
,![]()
; d) ![]()
,![]()
.
Znajdź punkty, których obrazami w jednokładności o środku

i stosunku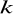
są punkty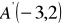
,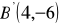
,
, gdy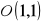
,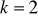
; b)
,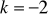
;
c) ![]()
,![]()
; d) ![]()
,![]()
.
Wyznacz środek jednokładności o stosunku

, w której obrazem punktu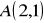
jest punkt
.Jakie przekształcenie określają wzory
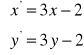
.Znajdź obrazy linii:
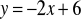
; b)
; c)
w jednokładności o środku ![]()
i stosunku ![]()
.
Dany jest trójkąt o wierzchołkach

,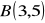
,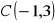
. Oblicz pole tego trójkąta.
Na płaszczyźnie dane są punkty:

,
,
,
. Przez punkt
poprowadzono prostą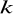
prostopadłą do prostej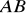
. Znajdź na prostej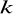
taki punkt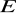
, by pola trójkątów
i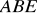
były równe.
Pole trójkąta o wierzchołkach
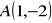
,
jest równe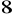
. Oblicz współrzędne trzeciego wierzchołka, wiedząc, że należy on do prostej o równaniu
.Narysuj elipsę o równaniu

; b)
.
Znajdź współrzędne jej ognisk.
Napisz równanie elipsy o środku w początku układu współrzędnych i wierzchołkach

,
.
Narysuj hiperbolę o równaniu.

; b)
.
Znajdź współrzędne jej ognisk.
Narysuj parabolę o równaniu

; b)
.
Znajdź współrzędne jej ogniska i równanie kierownicy
2
Wyszukiwarka