Rok akademicki: 1998/1999
|
Laboratorium fizyczne |
|||
Numer ćwiczenia: 72 |
TEMAT: Zjawisko Halla. |
|||
Wydział: elektronika Grupa: 1.2 |
Andrzej Kuliś |
|||
Data wykonania:
14. 04.1999 r. |
Ocena: |
Data zaliczenia: |
Podpis: |
|
|
Teoria: |
|
|
|
|
Sprawozdanie: |
|
|
|
1. Zasada pomiaru
Zjawisko Halla polega na powstawaniu pola elektrycznego E w płytce półprzewodnika, przez którą płynie prąd o gęstości j, umieszczonej w polu magnetycznym B:
![]()
![]()
Na powierzchniach bocznych płytki powstaje nadmiarowy ładunek - na jednej dodatni,
na drugiej ujemny, w wyniku czego powstaje dodatkowe pole elektryczne o natężeniu:
![]()
działające na elektrony siłą ![]()
skierowaną przeciwnie do siły Lorentza. Po ustaleniu się równowagi, FE=FL:
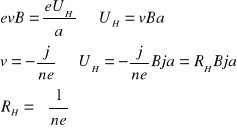
v -średnia prędkość elektronów
j - gęstość prądu w płytce
n - koncentracja elektronów
Stałą Halla RH (mającą znak ujemny w przypadku przewodnictwa „n”, lub dodatni dla przewodnictwa „p”), można wyznaczyć doświadczalnie ze wzoru:
![]()
![]()
b - grubość płytki
Przy znanej stałej Halla można obliczyć koncentrację elektronów swobodnych w metalu
lub elektronów przewodnictwa w półprzewodniku zdegenerowanym oraz ich ruchliwość, zwaną ruchliwość hallowską:
![]()
- opór właściwy materiału
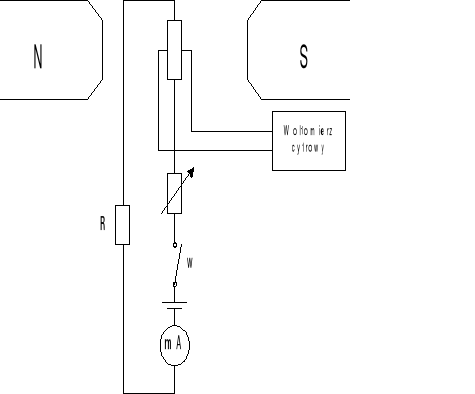
2. Układ pomiarowy
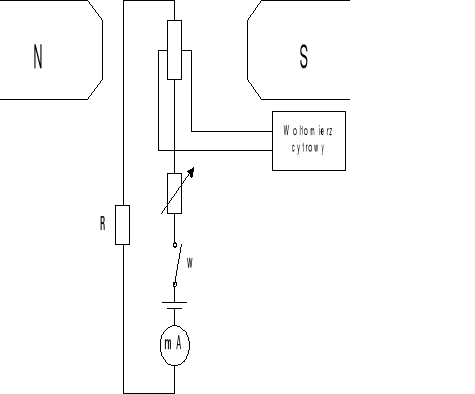
3. Ocena dokładności pojedynczych pomiarów
woltomierz cyfrowy:
ΔU= ± 0,05%
miliamperomierz:
- zakres: 30 mA
- podziałka: 30, 1 podziałka = 1 mA
- klasa: 0,5
4. Tabela parametrów
parametry próbki i warunki pomiarów efektu Halla:
Lp. |
Wielkość |
Wartość |
Błąd maksymalny |
Jednostka |
1 |
L |
5 |
0,1 |
[mm] |
2 |
A |
3 |
0,1 |
[Mm] |
3 |
B |
2 |
0,1 |
[μm] |
4 |
ρ |
0,0015 |
- |
[Ωm] |
5 |
B |
160 |
7,5 |
[mT] |
l - długość próbki
a - szerokość próbki
b - grubość próbki
- oporność właściwa
przenikalność magnetyczna 1
materiał - monokryształ Ge
typ przewodnictwa - n
5. Tabele pomiarów i obliczeń
Lp |
I |
-UH |
UH |
UHśr |
UHśr ⋅ I |
|
[mA] |
[mV] |
[mV] |
[mV] |
[mV ⋅ mA] |
1 |
2 |
0,34 |
0,45 |
0,39 |
0,79 |
2 |
3 |
0,49 |
0,65 |
0,57 |
1,71 |
3 |
4 |
0,67 |
0,86 |
0,76 |
3,06 |
4 |
5 |
0,8 |
1,08 |
0,94 |
4,7 |
5 |
6 |
0,99 |
1,27 |
1,13 |
6,78 |
6 |
7 |
1,17 |
1,5 |
1,33 |
9,34 |
7 |
8 |
1,33 |
1,71 |
1,52 |
12,16 |
8 |
9 |
1,48 |
1,92 |
1,7 |
15,3 |
9 |
10 |
1,65 |
2,15 |
1,9 |
19 |
10 |
11 |
1,8 |
2,31 |
2,05 |
22,6 |
11 |
12 |
2,01 |
2,6 |
2,3 |
27,66 |
12 |
13 |
2,15 |
2,79 |
2,47 |
32,11 |
13 |
14 |
2,3 |
2,98 |
2,64 |
36,96 |
14 |
15 |
2,48 |
3,18 |
2,83 |
42,45 |
Δ |
0,15 |
0,05 |
0,05 |
− |
− |
Σ |
− |
− |
− |
22,555 |
234,63 |
Lp |
I2 |
UHśr ⋅ ΔI |
I ⋅ ΔUHśr |
I ⋅ ΔI |
|
[mA2] |
[mV ⋅ mA] |
[mA ⋅ mV] |
[mA2] |
1 |
4 |
0,0593 |
0,000395 |
0,3 |
2 |
9 |
0,0855 |
0,000855 |
0,45 |
3 |
16 |
0,1148 |
0,001530 |
0,6 |
4 |
25 |
0,1410 |
0,002350 |
0,75 |
5 |
36 |
0,1695 |
0,003390 |
0,9 |
6 |
49 |
0,2003 |
0,004673 |
1,05 |
7 |
64 |
0,2280 |
0,006080 |
1,2 |
8 |
81 |
0,2550 |
0,007650 |
1,35 |
9 |
100 |
0,2850 |
0,009500 |
1,5 |
10 |
121 |
0,3083 |
0,011303 |
1,65 |
11 |
144 |
0,3458 |
0,013830 |
1,8 |
12 |
169 |
0,3705 |
0,016055 |
1,95 |
13 |
196 |
0,3960 |
0,018480 |
2,1 |
14 |
225 |
0,4245 |
0,021225 |
2,25 |
Σ |
1239 |
3,3833 |
0,117315 |
17,85 |
6. Obliczenia
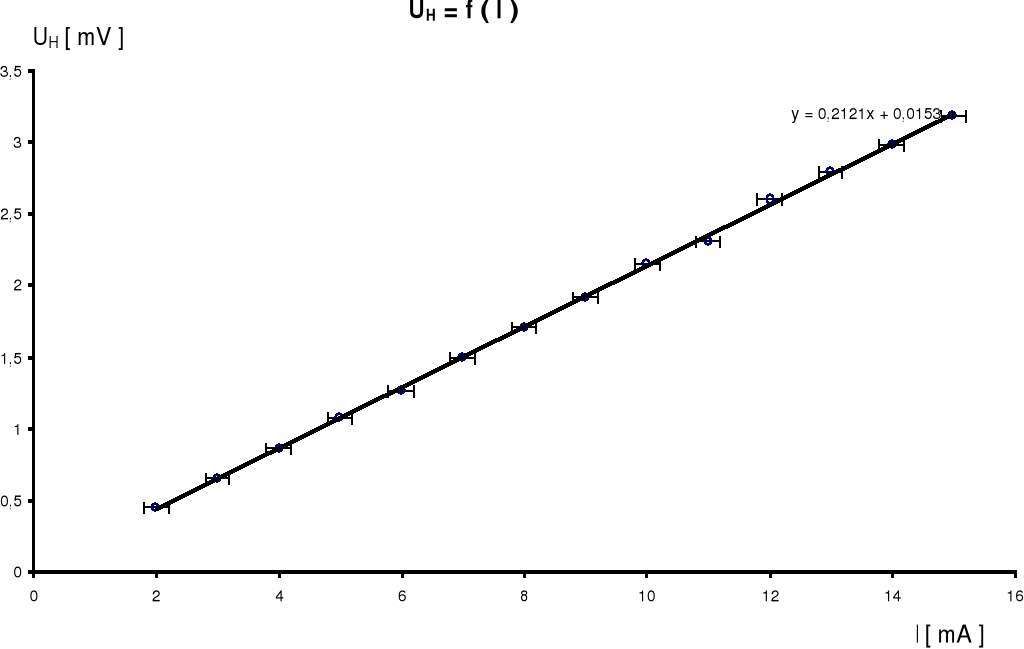
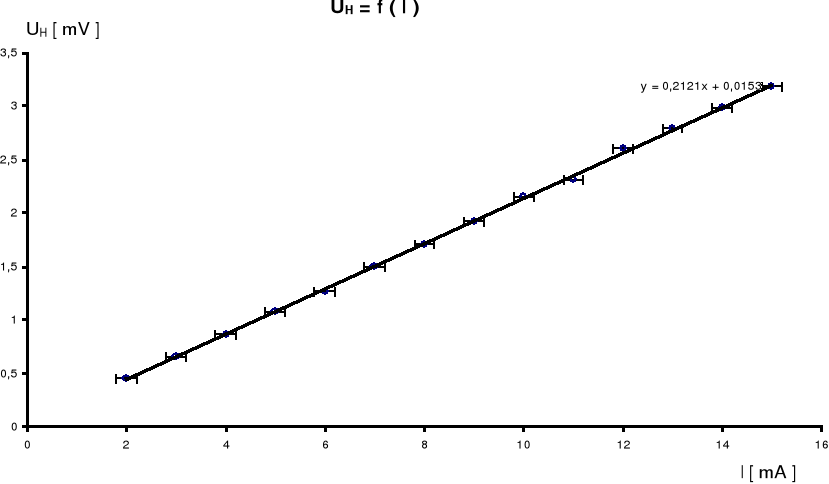
Współczynnik kierunkowy prostej:
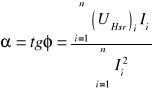
![]()
Obliczona wartość kąta nachylenia prostej nie różni się znacząco od rzeczywistego kąta nachylenia prostej podanego na wykresie.
Stała Halla:
![]()
![]()
Koncentracja elektronów:
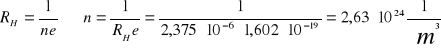
Ruchliwość nośników:
![]()
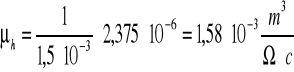
7. Dyskusja błędów
Wzór na błąd pomiaru stałej :
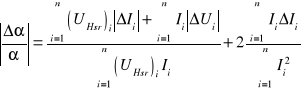
można uprościć do postaci:
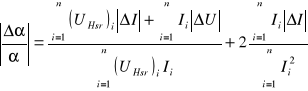
gdyż wszystkie pomiary zostały wykonane przy tych samych zakresach przyrządów.
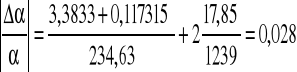
Stąd błąd pomiaru stałej Halla obliczony metodą różniczki logarytmicznej wynosi:
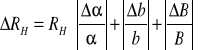
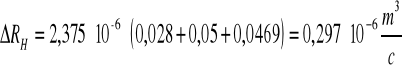
Zważywszy na warunki pomiarów, a zwłaszcza rozregulowany potencjometr do ustawianiprądu, błąd rzędu 10% wydaje się być zadawalający. Ponieważ koncentracja elektronów i ruchliwość nośników zależy tylko od stałej Halla, zatem błędy Δn i Δμ są również 10%.
Wynoszą odpowiednio : Δn= 0,263 1024 1/m3 Δμ= 0,158 10-3 m2/Ωc
8. Uwagi i wnioski
Zjawisko Halla pozwala określić znak ładunku płynącego w przewodniku. Zjawisko to obserwuje się we wszystkich przewodnikach i półprzewodnikach niezależnie od materiału z jakiego są wykonane. Zmiana na przeciwny kierunku prądu lub kierunku pola magnetycznego wywołuje zmianę znaku różnicy potencjałów. Wartość stałej Halla zależy od rodzaju materiału płytki, przy czym współczynnik ten jest dla jednych substancji dodatni, dla innych zaś - ujemny. Znak stałej Halla odpowiada znakowi ładunku nośników prądu. W związku z tym na podstawie wyników pomiaru stałej Halla dla półprzewodnika można wnosić o rodzaju jego przewodności. W przypadku przewodności elektronowej R<0, a w przypadku przewodności dziurowej R>0. Jeśli w półprzewodniku występują jednocześnie obydwa rodzaje przewodności, to na podstawie znaku stałej Halla można sądzić o tym, która z nich przeważa. W oparciu o stałą Halla można również określić gęstość nośników prądu, gdy znany jest rodzaj przewodności i ładunek nośników prądu. Obliczenie to zostało dokonane w naszym ćwiczeniu.
Wyszukiwarka