PROWADZĄCA ZAJĘCIA : Warszawa,07.10.2012r.
Grupa 5
TEMAT : „ OPORY PRZEPŁYWÓW”
Wykonali :
CEL ĆWICZENIA :
Celem ćwiczenia jest doświadczalne wyznaczenie strat ciśnienia występujących przy przepływie cieczy w przewodzie oraz porównanie otrzymanych wyników z wartościami obliczonymi teoretycznie
POMIARY :
odczyt z wodomierza
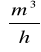
po 1 minucieodczyt spadku ciśnienia w poszczególnych układach :
obliczamy strumień objętości dla trzech przepływów , V [
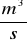
]wyznaczamy średnią prędkość liniową wody dla trzech przepływów , u [
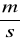
]obliczamy liczbę Reynoldsa dla trzech przepływów , Re
obliczamy wartość współczynnika λ dla trzech przepływów
obliczamy stratę ciśnienia w analizowanych układach pomiarowych - cząstkowe starty ciśnienia
obliczamy całkowite straty ciśnienia w analizowanych przepływach wg wzoru :
obliczamy całkowite teoretyczne straty ciśnienia w analizowanym rurociągu korzystając z równania :
PRZEPŁYWY |
ODCZYT 1 |
ODCZYT 2 |
ODCZYT 3 |
ODCZYT ŚREDNI |
1 |
0,0520 |
0,0510 |
0,0520 |
0,0517 |
2 |
0,0420 |
0,0442 |
0,0435 |
0,0432 |
3 |
0,0162 |
0,0168 |
0,0166 |
0,0165 |
PRZEPŁYWY |
CAŁY [mmHg] |
NA ZAWORZE [mmHg] |
NA ZWĘŻCE [mmHg] |
2 KOLANKA [mmCCl4] |
PROSTY ODCINEK [mmCCl4] |
1 |
205 |
14 |
215 |
552 |
117 |
2 |
118 |
10 |
122 |
328 |
70 |
3 |
25 |
3 |
26 |
78 |
20 |
OBLICZENIA :
V1 = 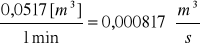
V2 = 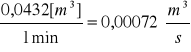
V3 = 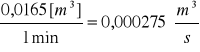
u1 = 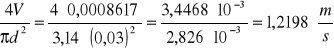
u2 = 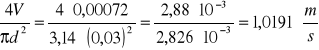
u3 = 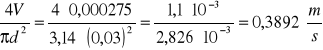
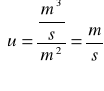
![]()
![]()
![]()
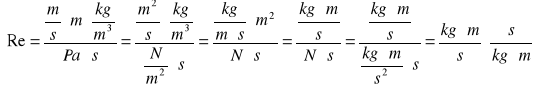
Ponieważ przepływ przez przewody jest burzliwy, współczynnik λ obliczymy ze wzoru Blasiusa, który jest prawdziwy dla 3 ∙ 103 <Re<105 : ![]()
![]()
![]()
![]()
* dla odczytów w [mmHg] wg wzoru : ![]()
* dla odczytów w [mmCCl4] wg wzoru : ![]()
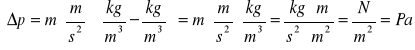
![]()
dla przepływu 1 :
Δp1 = 9,81 ∙ (13600 - 1000) ∙ 0,205 = 25 339 Pa = 25,3 kPa
Δp2 = 9,81 ∙ (13600 - 1000) ∙ 0,014 = 1 730,48 Pa = 1,7 kPa
Δp3 = 9,81 ∙ (13600 - 1000) ∙ 0,215 = 26 575,29 Pa = 26,6 kPa
Δp4 = 9,81 ∙ ( 1620 - 1000) ∙ 0,552 = 3 357,37 Pa = 3,4 kPa
Δp5 = 9,81 ∙ ( 1620 - 1000) ∙ 0,117 = 711,62 Pa = 0,7 kPa
dla przepływu 2 :
Δp1 = 9,81 ∙ (13600 - 1000) ∙ 0,118 = 14 585,51 Pa = 14,6 kPa
Δp2 = 9,81 ∙ (13600 - 1000) ∙ 0,010 = 1 236,06 Pa = 1,2 kPa
Δp3 = 9,81 ∙ (13600 - 1000) ∙ 0,122 = 15 079,93 Pa = 15,1 kPa
Δp4 = 9,81 ∙ ( 1620 - 1000) ∙ 0,328 = 1 944,96 Pa = 1,99 kPa
Δp5 = 9,81 ∙ ( 1620 - 1000) ∙ 0,070 = 425,75 Pa = 0,42 kPa
dla przepływu 3 :
Δp1 = 9,81 ∙ (13600 - 1000) ∙ 0,025 = 3 090,15 Pa = 3,1 kPa
Δp2 = 9,81 ∙ (13600 - 1000) ∙ 0,003 = 370,81 Pa = 0,4 kPa
Δp3 = 9,81 ∙ (13600 - 1000) ∙ 0,026 = 3 213,75 Pa = 3,2 kPa
Δp4 = 9,81 ∙ ( 1620 - 1000) ∙ 0,078 = 474,41 Pa = 0,5 kPa
Δp5 = 9,81 ∙ ( 1620 - 1000) ∙ 0,020 = 121,64 Pa = 0,1 kPa
![]()
dla przepływu 1 :
Δpstr = 1,7 + 0,7 ∙ 26,6 + 3,4 + 0,7 + ![]()
∙ 0,7 = 25,56 [kPa] poprawiałam
dla przepływu 2 :
Δpstr = 1,2 + 0,7 ∙ 15,1 + 1,99 + 0,4 + ![]()
∙ 0,4 = 14,81 [kPa]
dla przepływu 3 :
Δpstr = 0,4 + 0,7 ∙ 3,2 + 0,5 + 0,1 + ![]()
∙ 0,1 = 3,4 [ kPa]
![]()
[ Pa]
dla przepływu 1 :
Δpstr = 0,0228 ∙ ![]()
∙ ![]()
+ 0,3 ∙ ![]()
+ 32,65 ∙ ![]()
+ 2 ∙ 0,57 ∙ ![]()
= 27 877,11 [Pa] = 27,9 [kPa]
dla przepływu 2 :
Δpstr = 0,0239 ∙ ![]()
∙ ![]()
+ 0,3 ∙ ![]()
+ 32,65 ∙ ![]()
+ 2 ∙ 0,60 ∙ ![]()
= 19 574,32 [Pa] = 19,6 [kPa]
dla przepływu 3 :
Δpstr = 0,0304 ∙ ![]()
∙ ![]()
+ 0,3 ∙ ![]()
+ 32,65 ∙ ![]()
+ 2 ∙ 0,76 ∙ ![]()
= 2 952,26 [Pa] = 2,9 [kPa]
WNIOSKI :
Wraz ze wzrostem liczby Re rośnie strata ciśnienia spowodowana oporami przepływu.
ZAŁĄCZNIKI :
- wykres zależności Δp = f(Re)
Literatura :
Skrypt wydawnictwa SGGW „Inżynieria i aparatura przemysłu spożywczego. Ćwiczenia laboratoryjne. Część I”
![]()
Wyszukiwarka