Jakub Elsner Wrocław; 26 kwietnia 2010

Rok IV semestr 8

Prowadzący:

prof. dr hab. J. Chojcan

Ćwiczenie nr 3

Wyznaczanie czasu martwego licznika metodą dwu źródeł. Wstęp teoretyczny

1. Budowa i działanie licznika Geigera-Müllera

Licznik Geigera-Müllera składa się z cylindrycznej katody i przeciągniętej wzdłuż jej osi metalowej nici stanowiącej anodę. Elektrody zamknięte są w naczyniu wypełnionym gazem pod ciśnieniem 100 -200 mmHg. Kształt elektrod pozwala osiągnąć silnie niejednorodne pole elektryczne z największym natężeniem przy anodzie.

Mechanizm działania licznika jest bardzo złożony. Upraszczając można przedstawić go następująco: Jeśli do wnętrza licznika trafi np. cząstka alfa, to wywoła jonizację atomów gazu wzdłuż swojego toru ruchu. Powstałe w wyniku jonizacji elektrony i jony gazu przyspieszane są w polu elektrycznym, a następnie zderzają się z innymi atomami powodując dalsze jonizacje i w efekcie wyładowanie lawinowe podążające w stronę anody.

Wyładowanie to objawia się (w zewnętrznym obwodzie elektrycznym zamkniętym rezystorem R) powstaniem impulsu napięcia, będącym skutkiem wychwytywania przez cylindryczną katodę jonów gazu. Impuls ten przez kondensator kierowany jest do układu pomiarowego.

2. Licznik niesamogasnący

W procesie tworzenia się lawin elektronowych wzrasta również liczba jonów dodatnich, które jako znacznie cięższe od elektronów poruszają się wolniej i tworzą w gazie ładunek przestrzenny. Obecność ładunku przestrzennego zmniejsza natężenie pola elektrycznego w obszarze między anodą chmurą jonów przesuwająca się w kierunku anody. W wyniku tego zanika wyładowanie przez lawiny elektronowe. Jednakże jony dodatnie po osiągnięciu katody wybijają z niej elektrony i jeżeli tylko dodatni ładunek z katody zostanie dostatecznie szybko odprowadzony lawiny elektronowe zaczną się rozwijać od nowa. W ten sposób wyładowanie w liczniku jest stale podtrzymywane i licznik nie może rejestrować kolejnych cząstek promieniowania jądrowego.

3. Licznik samogasnący:

W liczniku samogasnącym stosuje się rozwiązania które powstrzymują ciągłe wyładowania w liczniku.

Jednym sposobem jest włączenie w obwód licznika dostatecznie dużego oporu R rzędu 10⁹ omów. Tak duży opór nie pozwala na szybkie odprowadzenie ładunku ujemnego z anody, co obniża jej potencjał aż do momentu gdy jony dodatnie zostaną zebrane na katodzie. To obniżenie potencjału oraz zmniejszenie napięcia między anodą i katodą, wystarcza aby elektrony wybite przez jony nie wywołały nowych lawin. Co skutkuje wygaśnięciem wyładowania. Po czasie rzędu setnej sekundy ładunek zostaje odprowadzony a licznik jest zdolny do zarejestrowania kolejnej cząstki.

Inny sposób wygaszania wyładowania polega na wypełnieniu licznika gazami z domieszką gazów lub par o cząsteczkach wieloatomowych ( metan, etan, pary alkoholu ). Przy odpowiedniej proporcji domieszki wyładowania po krótkim czasie wygasają same. Gaszenie następuje dzięki silnemu pochłanianiu promieniowania ultrafioletowego przez cząsteczki wieloatomowe oraz dzięki temu, że jony cząsteczek wieloatomowych nie wybijają z katody elektronów. Jeżeli rodzaj domieszki jest tak dobrany , ażeby energia jonizacji jej cząsteczek była mniejsza niż cząsteczek ( atomów ) gazu podstawowego, to przy zderzeniach jonów gazu podstawowego z cząsteczkami wieloatomowymi następuje jonizacja cząsteczek wieloatomowych. W rezultacie tego do katody będą docierały tylko jony domieszek nie wybijające elektronów.

4. Czas martwy licznika

Czas trwania impulsu, wywołanego pojedynczą cząstką, tzn. czas upływający od chwili rozpoczęcia wyładowania lawinowego do jego wygaśnięcia, nazywany jest czasem martwym licznika. Istotne jest, aby był on jak najkrótszy. Wówczas możliwe jest odróżnienie od siebie kolejnych, szybko po sobie nadlatujących cząstek. Wpływ na to ma zarówno konstrukcja elektrod (ich wielkość i odległość od siebie), ciśnienie mieszaniny gazów, jak i skład tej mieszaniny: np. pary alkoholu tłumią wyładowania. Czas martwy przeciętnego licznika jest rzędu stu mikrosekund.

5. Pomiar czasu martwego licznika G-M metodą dwu źródeł

Metoda polega na rejestrowaniu liczby zliczeń impulsów w danym czasie od dwu źródeł: 1 oraz 2 (w przybliżeniu podobnych), każdego z osobna i dla tych samych źródeł jednocześnie.

Jeżeli oznaczymy rzeczywistą liczbę cząstek trafiających w licznik w jednostce czasu z pierwszego źródła przez I₁, natomiast z drugiego przez I₂. Przy jednoczesnym działaniu obu źródeł liczba ta wynosi:

(1)

Przy czynnym tylko jednym źródle 1 (drugie usunięte) liczba rejestrowanych cząstek w jednostce czasu wyniesie:

(2)

Przy czynnym tylko drugim źródle 2 szybkość zliczeń wynosi:

(3)

Wreszcie przy czynnych obu źródłach (1,2) prędkość zliczeń wyniesie:

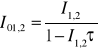
(4)

Wstawiając wzory (2), (3), (4) do wzoru (1) otrzymujemy:

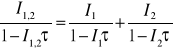
(5)

Rozwiązują to równanie względem τ i odrzucając wyrazy zawierające kwadrat małej wielkości τ otrzymujemy:

. (6)

Ponieważ określenie „czasu martwego” jest oparte na wyznaczeniu niewielkich różnic między dużymi wielkościami (licznik prawej strony wzoru (6)), to wielkości te muszą być wyznaczone ze szczególną dokładnością. W celu osiągnięcia odpowiedniej dokładności poszczególne pomiary winny być wykonane w ciągu odpowiednio długiego czasu. Należy zaznaczyć, że wyżej prowadzone rozważania są prawdziwe dla niezbyt dużych (w stosunku do 1/τ ) szybkości zliczeń, w praktyce unika się stosowania źródeł o dużych aktywnościach.

Jeżeli znamy τ dla danego układu pomiarowego, to zgodnie ze wzorem :

(7)

wyprowadzonym z podstawowych rozważań dotyczących różnicy pomiędzy potencjalną liczbą rejestracji N₀ w zadanym czasie t (I₀), a faktyczną N, w tym samym czasie t (I), wynikającą z istnienia czasu martwego można znaleźć związek pomiędzy I oraz I₀. Wygodnie jest, przy stałym używaniu tego samego licznika, mieć sporządzony wykres zależności

ρ = I₀/I od I.

Wtedy przy rejestrowaniu I można z wykresu znaleźć wartość ρ, a w konsekwencji faktycznie szukaną wartość I₀ ; ρ wskazuje ile razy większe jest I₀ od I, a jego odwrotność (1/ρ) nazywana jest wydajnością rejestracji (1/ρ < 1) związaną z czasem martwym.

Opracowanie wyników

a.

Moim zadaniem w tym doświadczeniu jest zmierzenie czasu martwego licznika Geigera-Müllera metodą dwu źródeł. W tym celu wykonałem pomiary zgodnie z instrukcjami do ćwiczenia, które przedstawiam w Tabeli 1 zamieszczonej poniżej.

Tabela 1
Źródła	Czynne źródła	Czas pomiaru t[min]	Liczba zliczeń N	Liczba zliczeń I w czasie minuty [min -1] (odjęte tło)
I para	1	13	84996	6527,153846
		2	8	81028	10117,5
		1+2	15	167496	11155,4
	II para	1	16	83026	5176,725
		2	20	89240	4449,6
		1+2	20	177432	8859,2

Tabela 1 w kolumnie „Liczba zliczeń I w czasie jednej minuty” zawiera wartości I obliczone po odjęciu tła. Pomiary tła zawiera Tabela 2.

Tabela 2
Pomiary tła:	Liczba zliczeń	Czas pomiaru [min]	Liczba zliczeń Itła w czasie minuty	Średnia Liczba zliczeń Itła
I para	336	28	12	11
		100	10		10
	II para	126	9		14	12,4
		108	10		10,8

Korzystając ze wzoru (6) obliczę „czasy martwe” licznika dla poszczególnych serii pomiarowych oraz ich niepewności, a następnie obliczę średnia czas martwy licznika.

Niepewności pomiarowe obliczyłem korzystając ze wzoru na złożoną niepewność standardową:

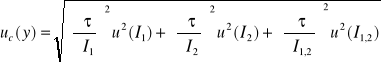
; gdzie:
(8)

W obliczeniach korzystałem z następujących przekształceń:

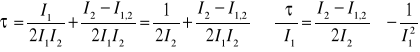
(9)

Wykonując bardzo podobne przekształcenia dla I₂ oraz I_1,2 otrzymałem:

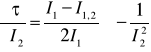
(10)

Wyniki obliczeń zamieszczam poniżej w Tabeli 3 zamieszczonej na następnej stronie.

Tabela 3
Źródła	Czas martwy licznika [min]
I para	4,156 (24) ·10^-5
II para	1,665 (62) ·10^-5
Średni „czas martwy”	2,910 (43) ·10^-5
„Czas martwy” z danych technicznych	3,333 ·10^-6

b.

Kolejnym zadaniem jest sporządzenie wykresu:

(11)

gdzie:
jest odwrotnością współczynnika wydajności.

Wykres znajduje się na końcu sprawozdania.

Wykres wykonałem, dla wartości zmiennej I z przedziału od 0 do 7000 [min^-1] z użyciem
uzyskanego z eksperymentu. Obliczyłem również i naniosłem na wykres niepewność pomiarową
obliczoną według wzoru:

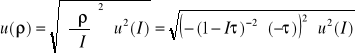
(12)

Jak widać dla każdej wielkości I dostaniemy inną wartość niepewności pomiarowej
.

Niestety nie mogłem nanieść na wykres niepewności pomiarowej osobno dla każdego punktu, dlatego zaznaczona na wykresie niepewność jest średnią z otrzymanych niepewności.

Niepewność naniesiona na wykres wynosi:
0,00213, i jest tak mała, że na wykresie widać ją jako pogrubienie otrzymanej krzywej. („linię pomocniczą” - omówię we wnioskach)

Poniżej w tabeli 3 przedstawiam niektóre obliczone wielkości potrzebne do sporządzenia wykresu
. Nie zamieszczam wszystkich ponieważ zajęły by zapewne kilka stron tego opracowania, a jest to bezcelowe.

Tabela 4
1	1,0000033	45	1,000150	400	1,001335	1000	1,003344
2	1,0000066	50	1,000167	450	1,001502	1500	1,005025
3	1,0000100	60	1,000200	500	1,001669	2000	1,006711
4	1,0000133	70	1,000233	550	1,001837	2500	1,008403
5	1,0000166	80	1,000267	600	1,002004	3000	1,010101
10	1,0000333	90	1,000300	650	1,002171	3500	1,011804
15	1,0000500	100	1,000333	700	1,002339	4000	1,013514
20	1,0000666	150	1,000500	750	1,002506	4500	1,015228
25	1,0000833	200	1,000667	800	1,002674	5000	1,016949
30	1,0001000	250	1,000834	850	1,002841	5500	1,018676
35	1,0001166	300	1,001001	900	1,003009	6000	1,020408
40	1,0001333	350	1,001168	950	1,003177	7000	1,023891

Wnioski

---