MIARY
|
|
|
|
|
Analiza klasyczna |
średnia
arytmetyczna- |
odchylenia: standardowe- Sx, przeciętne- Dx; współczynnik zmienności- Vx |
współczynnik asymetrii- Ax |
współczynnik skupienia (kurtoza)- K |
Analiza pozycyjna |
dominanta- Do; kwantyle: kwartyle- Q1, Q2 (Me), Q3, decyle |
rozstęp- R; odchylenie ćwiartkowe- SQ; współczynnik zmienności- VQ |
wskaźnik, współczynnik. skośności wg. Jule'a Candalla- AQ |
--- |
Miara połączona- |
wskaźnik, współczynnik asymetrii Pearsona- AS lub AD |
|
||
WZORY:
Szereg wyliczający:
![]()
, ![]()
, 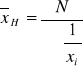
, ![]()
; Sx2=![]()
,
Dx=![]()
; Vx=![]()
lub Vx=![]()
;
Ax=![]()
, ![]()
; K=![]()
, ![]()
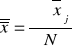
; S2=SM2+SW2; 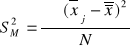
; ![]()
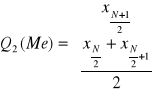
Q1=![]()
, Q3=![]()
; R=xmax-xmin; SQ=![]()
; VQ=![]()
AQ=![]()
; AS=![]()
lub AD=![]()
Szereg rozdzielczy punktowy:
![]()
, ![]()
, 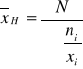
, ![]()
Sx2=![]()
, Dx=![]()
;
![]()
; ![]()
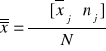
; 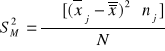
; ![]()
Pozostałe wzory (oprócz kwartyli) bez zmian
Szereg rozdzielczy przedziałowy:
![]()
, ![]()
, 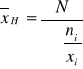
, ![]()
;
Sx2=![]()
, Dx=![]()
;
![]()
; ![]()
Do=![]()
lub Do=![]()
(przedziały równej długości)
Q1=x0+![]()
, Q2=x0+![]()
, Q3=x0+![]()
,
Pozostałe wzory bez zmian
Oznaczenia:
xi- wartość i-tej obserwacji
i=1,2 3….N; numery porządkowe obserwacji
N- liczebność próby, w szeregach rozdzielczych N=Σni
xmax- największa wartość obserwacji
xmin- najmniejsza wartość obserwacji
ni- liczba wystąpień i-tej wartości
∆i- długość i-tego przedziału
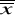
- średnia dla kilku grupj- numer grupy
nj- liczebność j-tej grupy
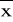
j- średnia w j-tej grupieSj- odchylenie w j-tej grupie
SM2- wariancja międzygrupowa
SW2- wariancja wewnątrzgrupowa
nicum liczebność skumulowana dla i-tego przedziału
ρi- gęstość i-tego przedziału
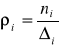
∆0- długość przedziału, do którego należy badana miara
x0- początek przedziału do którego należy badana miara
n0- liczebność w przedziale, do którego należy badana miara
n--liczebność w przedziale poprzednim do przedziału, do którego należy badana miara
n+- liczebność w przedziale następującym po przedziale, do którego należy badana miara
ρ0- gęstość w przedziale, do którego należy badana miara
ρ-- gęstość w przedziale poprzednim do przedziału, do którego należy badana miara
ρ+- gęstość w przedziale następującym po przedziale, do którego należy badana miara
ncum_- liczebność skumulowana dla przedziału poprzedzającego przedział, w którym jest dany kwartyl
UWAGI:
średnie: arytmetyczną i harmoniczną można stosować dla tych samych zjawisk; ich zastosowanie zależy od zadanych jednostek
z średniej geometrycznej korzysta się przy obliczaniu średniego tempa zmiany zjawisk (analiza dynamiki)
zmienność badanej próby uważa się za dużą gdy Vx(VQ)>10%
dominanta w szeregach wyliczających i rozdzielczych punktowych jest odczytywana jako wartość pojawiająca się w badanej próbie najczęściej (przy max ni); w szeregach rozdzielczych przedziałowych n0=max ni wskazuje przedział, do którego ona należy
dla rozkładów wielomodalnych lub skrajnych przyjęte jest nie wyznaczać dominanty
dominanta charakteryzuje tylko wartości typowe: xtypЄ(
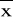
-Sx;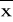
+Sx); xtypЄ(Me-SQ; Me+SQ)w szeregach wyliczających w przypadku gdy ¼ (¾)N są ułamkami pozycję kwartyla zaokrągla się zawsze do góry
w szeregach rozdzielczych punktowych kwartyle to pierwsze wartości xi dla których nicum≥ odpowiednio ¼N, ½N, ¾N, gdy ½N=nicum mediana jest (podobnie jak w szeregu wyliczającym) średnią arytmetyczną wartości xi oraz xi+1; w szeregach rozdzielczych przedziałowych powyższe postępowanie pozwala znaleźć przedział do którego należy dany kwartyl
wskaźnik skośności jest mianownikiem współczynnika asymetrii Jule'a Candalla albo Pearsona; (<0 oznacza asymetrię lewostronną, >0 prawostronną)
asymetria może być słaba (umiarkowana) gdy |Ax(AS, AD, AQ)|<0,8(1), lub silna (skrajna) gdy |Ax(AS, AD, AQ)|>0,8(1)
współczynnik asymetrii równy 0 oznacza rozkład symetryczny dl którego:
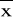
=Do=Merozkład uznaje się za spłaszczony bardziej od normalnego gdy K<3, za bardziej wysmukły gdy K>3. Dla K=3 rozkład ma ten sam stopień spłaszczenia co rozkład normalny
w szeregach rozdzielczych przedziałowych, w których występują przedziały otwarte (pierwszy lub ostatni) dopuszcza się ich domknięcie poprzez przyjęcie długości przedziałów sąsiednich w sytuacji gdy liczebność w tych przedziałach (lub przedziale) stanowi mniej niż 5%, ale więcej niż 1% całkowitej liczebności próby: 1%≤P=
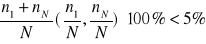
w sytuacji gdy wartość wskaźnika P nie przekracza 1% (P<1%) przedziałów otwartych nie bierze się pod uwagę w przeprowadzanej analizie
w sytuacji występowania przedziałów niedomkniętych nie można przeprowadzić analizy klasycznej, wyznacza się wtedy przybliżone miary
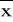
i Sx korzystając ze wzorów:(
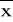
-Do)≈3(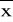
-Me); 2SX≈3SQw szeregach rozdzielczych zamiennie do ni można posłużyć się we wzorach (wykresach) częstością (wi) wyznaczaną ze wzoru: wi=
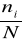
; W= Σwi
- 3 -
gdy N jest nieparzyste
gdy N jest parzyste
Wyszukiwarka