Politechnika Śląska
Wydział Mechaniczny Technologiczny
Mechanika i Budowa Maszyn
Grupa 6
Temat ćw.: Wyznaczanie energii maksymalnej promieniowania metodą absorpcyjną.
Sekcja 10
Paweł Śliwiak
Roman Zawisz
Krzysztof Szymiczek
I. Wprowadzenie :
Promieniowanie jądrowe może być wynikiem samorzutnego rozpadu niestabilnych jąder atomowych lub otrzymywane sztucznie podczas przyspieszenia cząstek naładowanych. Rozpad promieniotwórczy jest przemianą jądra w inne jądro o niższym stanie energetycznym , a przemianie towarzyszy emisja cząstek , elektronów (cząstek ) lub fali elektromagnetycznej ( promienie γ ) .
W czasie dt nastąpi rozpad :
![]()
jąder. Całkowanie tego wyrażenia daje prawo rozpadu promieniotwórczego :
![]()
,
gdzie: No - początkowa liczba jąder, N - liczba jąder, która pozostała po czasie t. Wielkość - jest nazywana stalą rozpadu i określa prawdopodobieństwo rozpadu jądra w czasie l s. Szybkość rozpadu charakteryzuje czas połowicznego zaniku T, po którym liczba jąder preparatu zmniejszy się dwukrotnie:
![]()
,
stąd:
![]()
Średni czas życia pojedynczego jądra jest równy odwrotności stałej rozpadu :
![]()
.
Wielkością charakteryzującą preparaty jest ich aktywność :
![]()
,
równa liczbie rozpadów w jednostce czasu. Jednostką aktywności źródeł promieniotwórczych jest l Kiur (Ci),odpowiadający liczbie 3,7 * 1010 rozpadów w 1s. Inna jednostka aktywności - l rutherford - odpowiada liczbie zliczeń l06 s-1.
Naturalne rozpady promieniotwórcze zachodzą z emisją jednego z trzech rodzajów promieniowania :
1) promieniowania
2) promieniowania :
a) rozpad negatonowy
b) rozpad pozytonowy
c) wychwyt elektronu
3) promieniowanie γ
Większość występujących w naturze pierwiastków promieniotwórczych powiązana jest ze sobą w tzw. rodziny promieniotwórcze: torową, neptunową, uranową i aktynową. Warunkiem istnienia w przyrodzie izotopu jest to, aby jego czas życia był porównywalny z wiekiem Ziemi (ok.109 lat).
Energia emitowanych cząstek osiąga wartości od zera do pewnej wartości maksymalnej, a widmo energetyczne ma charakter ciągły. Zgodnie z zasadą zachowania energii, część energii powinna przejmować neutralna cząstka o niewielkiej masie. Taką cząstką jest neutrino, a antycząstką - antyneutrino. Energia cząstek może osiągać wartości od 10 keV do 10 MeV. Największą energię posiadają cząstki w przypadku, gdy rozpad zachodzi bez udziału neutrino (bądź antyneutrino).
Dokładne pomiary energii cząstek oparte są na pomiarze odchylenia ich toru w polach
magnetycznych w spektrometrach z polem płaskim lub z ogniskowaniem. Mniej dokładna metoda pomiaru energii cząstek polega na wyznaczeniu zasięgu. Stosując liczniki proporcjonalne osiąga się zdolność rozdzielczą 12%, dla liczników Geigera - Mullera osiąga się gorsze wyniki.
Celem ćwiczenia jest wyznaczenie energii maksymalnej promieni metodą absorpcyjną. Proces przejścia promieni przez absorbującą substancję jest złożony.
Elektrony mogą być usuwane z wiązki wskutek:
jonizacji,
zderzeń sprężystych z elektronami i jądrami,
zderzeń niesprężystych i związanego z nimi promieniowania hamowania.
II. Przebieg ćwiczenia:
1. Włączamy przelicznik.
2. Mierzymy tło licznika (pomiar liczby zliczeń w czasie 10 min przy nieobecności preparatu).
Preparat promieniotwórczy umieszczamy w domku ołowianym w odległości ok. l cm od okienka licznika.
3. Preparat ujmujemy szczypcami i wstawiamy razem z podstawką w wycięcie pierścienia wstawionego uprzednio w szczelinę domku ołowianego. Preparat umieszczamy otworem do góry.
4. Nastawiamy tryb pomiaru czasu zliczania [s] zadanej liczby impulsów, np. l O4.
5. Pomiary wykonujemy najpierw bez absorbenta, a następnie z płytkami aluminiowymi dokładanymi na stos na preparat.
Zaleca się rozpoczęcie pomiarów od najcieńszych płytek. W miarę zwiększania się czasu można zmniejszyć zadaną liczbę impulsów (po uzgodnieniu z prowadzącym zajęcia).
III. Obliczenia:
Tabelka pomiarowa:
Tło [ 10 min ] = 68 N'=6,8 [1/min] ln(N')=1,92
d=0,0289mm ≈ 0,03mm - grubość jednej folii aluminiowej
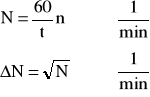
L.P. |
Grubość d[mm] |
Impulsy N |
Czas t[s] |
N'[imp/min] |
ΔN' |
1 |
0 |
10000 |
82.82 |
7244.63 |
86 |
2 |
0.03 |
10000 |
109.10 |
5499.54 |
75 |
3 |
0.06 |
10000 |
134.33 |
4466.61 |
67 |
4 |
0.09 |
10000 |
143.45 |
4182.64 |
65 |
5 |
0.11 |
10000 |
148.10 |
4051.32 |
64 |
6 |
0.14 |
10000 |
157.02 |
3821.17 |
62 |
7 |
0.20 |
1000 |
21.90 |
2739.73 |
53 |
8 |
0.26 |
1000 |
34.70 |
1729.11 |
42 |
9 |
0.31 |
1000 |
46.40 |
1293.10 |
36 |
10 |
0.37 |
1000 |
57.30 |
1047.12 |
33 |
11 |
0.43 |
1000 |
68.20 |
879.77 |
30 |
12 |
0.51 |
1000 |
86.50 |
693.64 |
27 |
13 |
0.60 |
1000 |
110.80 |
541.52 |
24 |
14 |
0.68 |
1000 |
131.09 |
457.70 |
22 |
15 |
0.77 |
1000 |
170.40 |
352.11 |
19 |
16 |
0.86 |
1000 |
264.00 |
227.27 |
16 |
Wykonujemy wykres zależności szybkości zliczeń N' od grubości absorbenta d[mm]:
N'=f(d).
Obliczamy ln(N') i na podstawie poniższej tabelki wykonujemy wykres zależności logarytmu naturalnego szybkości zliczeń od grubości zbsorbentu, oraz od promieniowania tła:
ln(N')=f(d)
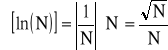
Tabela wyników:
L.P. |
Grubość d[mm] |
N'[imp/min] |
ln(N') |
Δln(N') |
1 |
0 |
7244.63 |
8.8880154 |
0.012 |
2 |
0.03 |
5499.54 |
8.61242 |
0.014 |
3 |
0.06 |
4466.61 |
8.4043855 |
0.015 |
4 |
0.09 |
4182.64 |
8.3386984 |
0.016 |
5 |
0.11 |
4051.32 |
8.3067972 |
0.016 |
6 |
0.14 |
3821.17 |
8.2483117 |
0.017 |
7 |
0.20 |
2739.73 |
7.9156132 |
0.02 |
8 |
0.26 |
1729.11 |
7.4553602 |
0.025 |
9 |
0.31 |
1293.10 |
7.1648004 |
0.028 |
10 |
0.37 |
1047.12 |
6.9537992 |
0.032 |
11 |
0.43 |
879.77 |
6.7796553 |
0.035 |
12 |
0.51 |
693.64 |
6.5419554 |
0.039 |
13 |
0.60 |
541.52 |
6.2943731 |
0.045 |
14 |
0.68 |
457.70 |
6.1262157 |
0.049 |
15 |
0.77 |
352.11 |
5.8639512 |
0.054 |
16 |
0.86 |
227.27 |
5.4261507 |
0.071 |
L.p. |
d [mm] |
d-d |
d+d |
N-N |
N+N |
ln(N-N) |
ln( |
1 |
0 |
0 |
0 |
7259,51 |
7329,25 |
8,89 |
8,9 |
2 |
0,03 |
0,02985 |
0,03015 |
5425,38 |
5573,7 |
8,599 |
8,626 |
3 |
0,06 |
0,05971 |
0,06029 |
4399,78 |
4533,44 |
8,389 |
8,419 |
4 |
0,09 |
0,08956 |
0,09044 |
4117,97 |
4247,31 |
8,323 |
8,354 |
5 |
0,11 |
0,10941 |
0,11059 |
3987,67 |
4114,97 |
8,291 |
8,322 |
6 |
0,14 |
0,13927 |
0,14074 |
3759,35 |
3882,99 |
8,232 |
8,264 |
7 |
0,2 |
0,19897 |
0,20103 |
2687,39 |
2792,07 |
7,896 |
7,935 |
8 |
0,26 |
0,25868 |
0,26132 |
1687,53 |
1770,69 |
7,431 |
7,479 |
9 |
0,31 |
0,30838 |
0,31162 |
1257,14 |
1329,06 |
7,137 |
7,192 |
10 |
0,37 |
0,36809 |
0,37191 |
1014,76 |
1079,48 |
6,922 |
6,984 |
11 |
0,43 |
0,4278 |
0,43221 |
850,11 |
909,43 |
6,745 |
6,813 |
12 |
0,51 |
0,50735 |
0,51265 |
667,3 |
719,98 |
6,503 |
6,579 |
13 |
0,6 |
0,59691 |
0,60309 |
518,25 |
564,79 |
6,25 |
6,336 |
14 |
0,68 |
0,67603 |
0,68397 |
436,31 |
479,09 |
6,078 |
6,172 |
15 |
0,77 |
0,76603 |
0,77397 |
333,35 |
370,87 |
5,809 |
5,916 |
16 |
0,86 |
0,85559 |
0,86441 |
212,19 |
242,35 |
5,357 |
5,49 |
Regresja liniowa:
Liczba pomiarów n= |
16 |
Współczynnik a= |
-3.89 [1/mm] |
Współczynnik b= |
8.65 [1/mm] |
Błąd Sa= |
0.16 [1/mm] |
Błąd Sb= |
0.07 [1/mm] |
Wsp. korelacji |
-0.99 |
Czyli równanie zależności ln(N')=f(d) ma postać:
ln(N')=-(3,89±0,16)*d+(8,65±0.07)
Wyznaczenie zasięgu liniowego promieniowania :
Odczytuję zasięg liniowy z wykresu:
![]()
Obliczenie zasięgu masowego.
Gęstość aluminiu wynosi ρ=2700 ![]()
.

Określam energię maksymalną promieni stosowanego preparatu Tl204.
Na podstawie poniższej tabeli narysuję wykres zależności energii maksymalnej promieniowania beta od zasięgu masowego:
Tabela 1
ZM. [mg/cm2] |
E [MeV] |
13.5 |
0.1 |
26.5 |
0.15 |
42 |
0.2 |
59 |
0.25 |
78 |
0.3 |
120 |
0.4 |
165 |
0.5 |
310 |
0.8 |
420 |
1 |
520 |
1.2 |
680 |
1.5 |
Posłużę się tu metodą graficzną. Odczytana wartość energii maksymalnej wynosi:
![]()
![]()
IV. Analiza błędów.
Wykonując pojedynczy pomiar liczby zliczeń przy pomocy przelicznika można temu pomiarowi przypisać błąd średni równy pierwiastkowi kwadratowemu z liczby zliczeń N:
![]()
Błąd bezwzględny oznacza odchylenie wyniku pomiaru od wartości rzeczywistej i podawany jest w jednostkach wielkości mierzonej , w naszym przypadku X= ![]()
![]()
= 1). 7244.6386 ,pozostałe wartości podane w tabeli pomiarowej.
Błąd względny wyrażony jest stosunkiem błędu bezwzględnego do wielkości mierzonej :
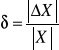
BŁĄD WZGLĘDNY [%]
Przy pomiarach ,gdzie liczba zliczeń jest równa 10000 błąd względny jest równy 1%.
V. Wnioski.
Wykonane ćwiczenie wykazało, że pochłanianie energii promieniowania jest zależne od grubości absorbenta, którym jest w naszym przypadku aluminium. Poprzez zwiększanie grubości absorbenta liczba przenikających przez absorbent cząstek maleje (wykres 1). Nie jest możliwe, aby szybkość zliczeń była zerowa. Spowodowane jest to zawartością substancji promieniotwórczych w powietrzu, budową licznika, promieniowaniem kosmicznym.
Porównując otrzymaną wartość z wartością tablicową izotopu 204Tl (E=0,8 MeV) należy stwierdzić, iż w zakresie przez nas wyznaczonym różni się od wartość tablicowej.
Sprawozdanie z fizyki
1
Wyszukiwarka