Spostrzeżenia pośredniczące. Równania poprawek i równania normalne
Jeżeli do wyznaczenia pewnych niewiadomych wielkości x, y, z,..., t, które nie mogą być wyznaczone bezpośrednio, obserwujemy szereg wielkości dostępnych ![]()
, aby za ich pośrednictwem, przez odpowiednie związki matematyczne, obliczyć poszukiwane niewiadome x, y, z,..., t, to mówimy wówczas, że spostrzeżenia ![]()
są spostrzeżeniami pośredniczącymi.
Wyznaczenie niewiadomych x, y, z,..., t jest tylko wtedy możliwe, jeżeli n = u, gdzie u to liczba spostrzeżeń niezbędnych do określenia wielkości wyznaczanych, czyli liczba niewiadomych, a n to liczba spostrzeżeń dokonanych. Możliwość wyrównania jest uwarunkowana istnieniem spostrzeżeń nadliczbowych, tj. przypadkiem, gdy u<n. Metoda wyrównania spostrzeżeń pośredniczących powinna jednocześnie spełniać warunek wyrażony wzorem
[vv] = minimum lub [pvv] = minimum.
Spostrzeżenia wyrównane tą metodą określamy za pośrednictwem niewiadomych wzorem
![]()
(1)
gdzie i - kolejne spostrzeżenie w wyrównywanym układzie, zaś vi - poprawka jaką należy dodać do spostrzeżenia, czyli do wielkości pomierzonej Li.
Przed wyrównaniem znamy tylko przybliżone wartości niewiadomych ![]()
różniące się od niewiadomych o niewielkie poprawki ![]()
. Wobec tego równanie (1) przyjmie postać
![]()
lub
![]()
Równanie typu (2) nazywamy równaniem poprawek w postaci ogólnej lub pierwotnej. Jeżeli funkcja F nie jest funkcją liniową, należy ją rozwinąć na szereg Taylora w otoczeniu wartości ![]()
. A zatem
![]()
(2)
Przez Ri oznaczono dalsze wyrazy szeregu Taylora, które można odrzucić, jeżeli przybliżenia wielkości niewiadomych ![]()
są wystarczająco bliskie wartościom najprawdopodobniejszym.
Równania poprawek przyjmują zatem postać liniową
![]()
Równanie to przedstawiamy w postaci
![]()
gdzie ![]()
- współczynniki równania poprawek równe pochodnym cząstkowym funkcji F względem poszczególnych niewiadomych po podstawieniu do nich wartości przybliżonych ![]()
; ![]()
- różnice między wartościami wyrównanymi niewiadomych a ich wartościami przybliżonymi;![]()
- poprawki wyrównawcze poszczególnych spostrzeżeń;![]()
wyrazy wolne.
Wyraz wolny równań poprawek jest to różnica między przybliżoną a pomierzoną wartością spostrzeżenia:
![]()
Równań poprawek będzie zawsze tyle, ile wykonaliśmy spostrzeżeń, poprawki bowiem ![]()
są błędami pozornymi dla n dokonanych spostrzeżeń pośredniczących.
Przybliżone wartości niewiadomych ![]()
obliczamy przed przystąpieniem do wyrównania na podstawie dokonanych spostrzeżeń pośredniczących.
Bardzo często równania poprawek mają od razu postać liniową i wówczas nie trzeba dokonywać żadnych dodatkowych działań matematycznych, lecz dla uniknięcia działań na dużych liczbach podstawiamy jak poprzednio ![]()
![]()
![]()
…Jako nowe niewiadome wystąpią wówczas w równaniach poprawek zawsze niewielkie wartości ![]()
; Równania poprawek w liczbie n o postaci
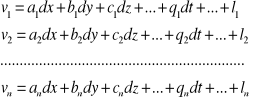
nie dają możliwości obliczenia różnic ![]()
, ponieważ mamy tu n poprawek v i u niewiadomych różnic ![]()
zatem w sumie n + u niewiadomych, a tylko n równań. Problem ten rozwiązujemy w następujący sposób. Podstawowe wymaganie metody najmniejszych kwadratów [vv] = minimum będzie spełnione, jeżeli pierwsze pochodne funkcji ![]()
w stosunku do kolejnych zmiennych niezależnych będą równe zeru, czyli
![]()
![]()
![]()
Jeżeli każde równanie poprawek podniesiemy do kwadratu i zsumujemy, to rozpatrując dla przykładu układ 3 równań (n = 3), otrzymamy jedno równanie kształtu:
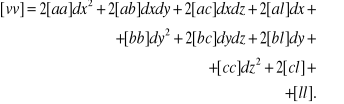
Kolejne pochodne cząstkowe tego równania w stosunku do trzech zmiennych są następujące
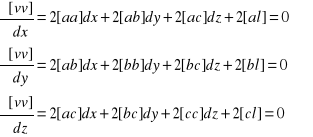
z czego po podzieleniu przez 2 otrzymujemy 3 tzw. równania normalne o 3 niewiadomych:
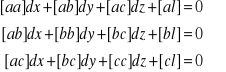
,
Rozwiązanie tych równań da nam jednoznaczne wartości niewiadomych ![]()
, wobec czego wartości najprawdopodobniejsze szukanych elementów znajdziemy za pomocą równań
![]()
![]()
![]()
Równań normalnych jest oczywiście zawsze tyle, ile niewiadomych. Jeżeli obserwacje ![]()
, są niejednakowo dokładne, to każdemu z równań poprawek należy przypisać odpowiednią wagę
![]()
z wagą ![]()
a równania normalne przyjmą wówczas postać
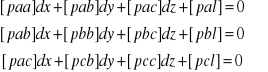
Uwaga: Często dla prostoty zapisu zastępujemy wyrażenia ![]()
. przez x, y, z, ...
Rozpatrzmy sposób układania równań normalnych na przykładzie. Dla uproszczenia przyjmujemy trzy niewiadome x, y, z oraz 6 obserwacji niejednakowo dokładnych. Przy obserwacjach jednakowo dokładnych mielibyśmy p = 1. Przybliżone wartości niewiadomych ![]()
oblicza się najprostszą drogą przed przystąpieniem do wyrównania. Jeżeli funkcję rozwijamy na szereg Taylora, to przybliżone wartości niewiadomych należy liczyć z takich zależności, aby wartości różnic ![]()
były możliwie małe.
Wyszukiwarka