Politechnika Łódzka Filii
W Bielsku-Białej
Ul. Willowa 2
Ćwiczenie nr 56
Pomiar zależności oporności metali
i półprzewodników od temperatury.
Grupa 503
Przemyław Leguła
Wojciech Komendera
Grzegorz Wrażeń
I. Wprowadzenie teoretyczne i opis stanowiska doświadczalnego :
Model pasmowy przewodnictwa.
Ze względu na przewodnictwo elektryczne wszystkie ciała dzielimy na : izolatory, przewodniki i półprzewodniki. Izolatory są bardzo złymi przewodnikami. Przewodniki mają bardzo mały opór właściwy rzędu 10-8-10-6 . Opór właściwy półprzewodników mieści się w bardzo szerokich granicach od 10-7 do 108 , lecz nie sama wartość oporu właściwego jest podstawą klasyfikacji. Istotnym czynnikiem jest temperaturowa zależność oporu elektrycznego .
W przewodnikach opór rośnie wraz ze wzrostem temperatury jest do niej proporcjonalny co można zapisać wzorem
R=αT
R- opór T- temperatura α -stała zależna od kształtu i rozm. próbki
Pełny wzór przedstawiający zależność oporu od temperatury jest następujący
R=R0(1+ΔT)
![]()
gdzie. Ro- opór elektryczny przewodnika w temperaturze otoczenia;
ΔT- przyrost temperatury;
α-temperaturowy współczynnik rezystancji
zależność przedstawiona powyżej jest zależnością liniową i można ją zapisać następująco
y= ax +b
gdzie y= R/R0 , a=α , x=၄T , b=1
co ułatwi obliczenie temperaturowego współczynnika rezystancji α.
Zwiększenie oporności metali przy wzroście temperatury tłumaczy się wzrostem rozproszenia cieplnego elektronów na jonach siatki krystalicznej.
Półprzewodniki zachowują się z koleji odwrotnie niż w/w przewodniki , opór elektryczny maleje ze wzrostem temperatury . Wynika to z tego iż przewodniki są kryształami i w temperaturze 0 K w sieci krystalicznej nie istnieją (lub są w ilościach ''śladowych") wolne elektrony mogące przewodzić prąd elektryczny . Dopiero ze wzrostem temperatury elektrony są termicznie wzbudzane i przechodzą de pasma przewodnictwa umożliwiając tym samym przepływ prądu elektrycznego.
Zależność oporu od temperatury dla półprzewodników opisuje wzór
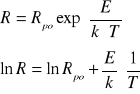
E - szerokość pasma wzbronionego
k - stała Boltzmann'a (k=1,38⋅10-23 [J/K]);
Rpo - stała oporności.
równanie to sprowadza się również do równania liniowego
y=ax+b
gdzie y= ln R , a= E/k , x=1/T b=lnRp0
Teoria pasmowa ciał stałych - opisuje zmianę poziomów energetycznych atomów lub cząstek w przypadku utworzenia przez nich struktury krystalicznej. W swobodnych atomach elektrony nie mogą mieć dowolnych wartości energii lecz przyjmują niektóre wartości dozwolone przez reguły kwantowe, tzn. Że poziomy energetyczne są oddzielone od siebie dość szerokimi odstępami o wzbronionych wartościach energii. Często energetyczne poziomy dozwolone przedstawiamy za pomocą poziomych kresek. Osią rzędnych jest energia. Położenie każdej kreski oznacza energię danego stanu. Odstępy między kreskami odpowiadają wzbronionym wartościom energii.
a) b)
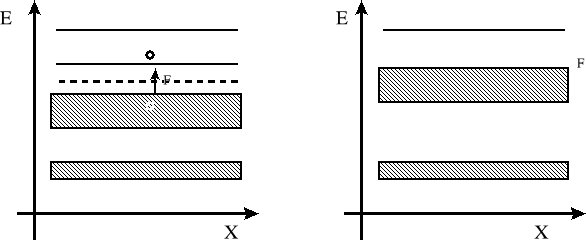
Rys.1. Model pasmowy : a) półprzewodnika, b) przewodnika.
Półprzewodnictwo samoistne.
Czysty, zbliżony do idealnego kryształ półprzewodnika wykazuje przewodnictwo samoistne.
Schemat pasm energetycznych półprzewodnictwa samoistnego w temp. 0 K przewodnictwo jest równe zeru, wszystkie stany w paśmie walencyjnym są zapełnione i wszystkie stany w paśmie przewodnictwa są puste. Gdy rośnie temperatura, przewodnictwo również wzrasta, gdyż elektrony są termicznie wzbudzone do pasma przewodnictwa. (rys.1a.)
Przewodnictwo domieszkowe.
Kryształ rzeczywisty różni się od idealnego tym, że występują w nim centra domieszkowe tzw. defekty punktowe.
Centra domieszkowe mogą być kilku typów charakteryzujących się :
występowaniem obcych atomów,
odstępstwami od składu stechiometrycznego (pewnych atomów może być więcej a innych mniej),
pustymi węzłami w sieci krystalicznej,
dodatkowymi atomami lub jonami w obszarach międzywęzłowych,
możliwe są też defekty liniowe lub śrubowe, tzw. dyslokacje.
II. Praktyczne wykonanie ćwiczenia :
Przyrządy:
-termostat;
-płytki z badanymi elementami w kąpieli olejowej;
-omomierz;
-termometr;
Do wyprowadzeń badanych elementów umieszczonych w termostacie przyłączono przygotowane urządzenia do pomiaru oporności (omomierze). Odczytano temp. początkową kąpieli olejowej T0 i zmierzono wartość oporności początkowych R0 badanych elementów. Następnie włączono grzałkę na maksymalną moc. Gdy temperatura kąpieli olejowej osiągnęła pełną wartość (25oC) dokonano kolejnych pomiarów, w 5-cio stopniowych odstępach między kolejnymi wartościami temperatury oleju. Badania zakończono przy temp.80 oC. Następnie wyłączono ogrzewanie kąpieli. Zmierzone wartości badanych parametrów umieszczono w tabelach.
III. Wyniki pomiarów oraz obliczeń :
1)Przewodnik:
l.p. |
t |
ΔT |
R |
ΔR |
R/R0 |
|
[0C] |
[K] |
[Ω] |
[Ω] |
|
1 |
21,6 |
0 |
17,57 |
0 |
1 |
2 |
26,6 |
5 |
17,82 |
0,25 |
1,014 |
3 |
31,6 |
10 |
18,13 |
0,31 |
1,031 |
4 |
36,6 |
15 |
18,46 |
0,33 |
1,05 |
5 |
41,6 |
20 |
18,79 |
0,33 |
1,069 |
6 |
46,6 |
25 |
19,13 |
0,34 |
1,088 |
7 |
51,6 |
30 |
19,49 |
0,36 |
1,109 |
8 |
56,6 |
35 |
19,86 |
0,37 |
1,13 |
9 |
61,6 |
40 |
20,21 |
0,35 |
1,15 |
10 |
66,6 |
45 |
20,51 |
0,36 |
1,17 |
11 |
71,6 |
50 |
20,92 |
0,35 |
1,19 |
12 |
76,6 |
55 |
21,25 |
0,33 |
1,209 |
13 |
81,6 |
60 |
21,60 |
0,35 |
1,229 |
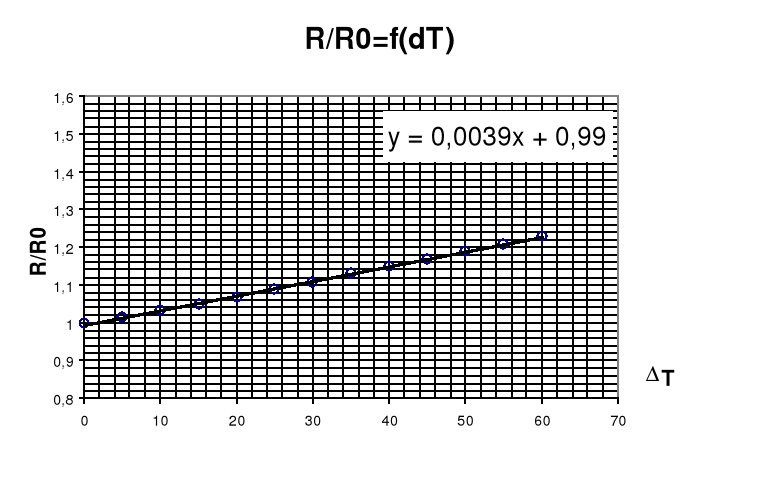
L.p. 1 - odpowiada pomiarowi w temperaturze otoczenia.
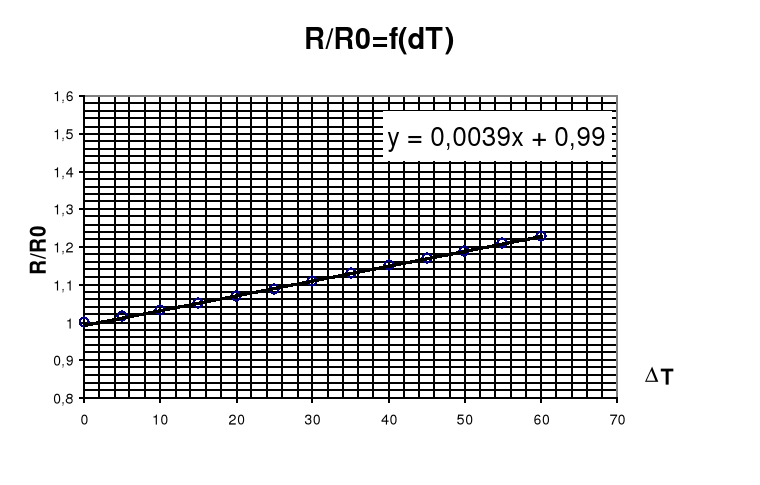
Współczynnik prostej regresji a
a = 0,0039; Δa = 0,000036; [K-1]
α = a = 0,0039 [K-1]
R/R0(ΔT=0) |
α±Δၡ |
|
[K-1] |
1 |
0,0039Ⴑ0,000039 |
2)Półprzewodnik:
l.p. |
t |
T |
1/T |
R |
ΔR |
ln R |
|
[oC] |
[K] |
[K-1] |
[kΩ] |
[kΩ] |
|
1 |
21,6 |
294,75 |
0,00339 |
10,58 |
0 |
2,31 |
2 |
26,6 |
299,75 |
0,00334 |
8,55 |
-2,03 |
2,15 |
3 |
31,6 |
304,75 |
0,00328 |
6,71 |
-1,84 |
1,9 |
4 |
36,6 |
309,75 |
0,00323 |
5,37 |
-1,34 |
1,68 |
5 |
41,6 |
314,75 |
0,00318 |
4,3 |
-1,07 |
1,46 |
6 |
46,6 |
319,75 |
0,00313 |
3,53 |
-0,77 |
1,26 |
7 |
51,6 |
323,75 |
0,00308 |
2,89 |
-0,64 |
1,06 |
8 |
56,6 |
329,75 |
0,00303 |
2,39 |
-0,5 |
0,87 |
9 |
61,6 |
334,75 |
0,00299 |
2,0 |
-0,39 |
0,71 |
10 |
66,6 |
339,75 |
0,00294 |
1,71 |
-0,29 |
0,54 |
11 |
71,6 |
344,75 |
0,0029 |
1,46 |
-0,25 |
0,38 |
12 |
76,6 |
349,75 |
0,00286 |
1,26 |
-0,2 |
0,23 |
13 |
81,6 |
354,75 |
0,00282 |
1,1 |
-0,16 |
0,1 |
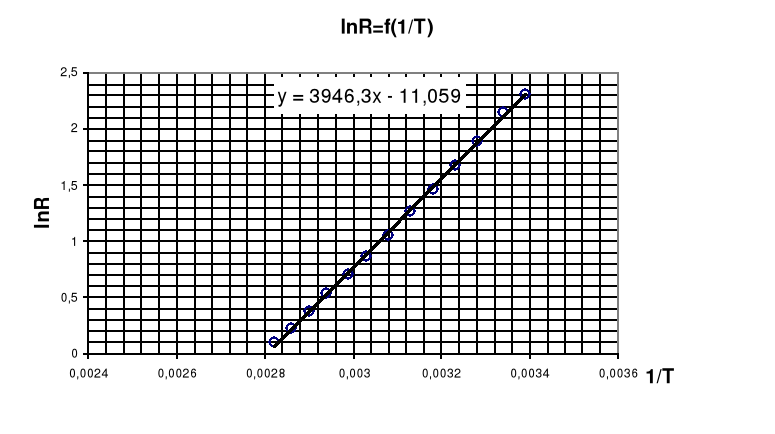
Współczynnik prostej regresji a
a = 3946,3 Δa = 41,27 [K]
E/k = a ⇒ E = k⋅a = 1,38⋅10-23 ⋅ 3946,3 = 0,54 10-19[J]
1eV = 1,602⋅10-19
E=(0,54 10-19 )/(1,602 10-19)=0,34 [eV]
lnRpo =b ⇒ Rpo = eb = e -11,059 = 1,63 10-5 [kΩ]
RpoႱ ၄Rpo |
E/k |
E |
[kၗ] |
[K] |
[eV] |
(1,63Ⴑ0,031) 10-5 |
3946,3 |
0,34 |
V . Wnioski :
Rezystancja przewodnika rośnie (nieznacznie) wraz ze wzrostem temperatury,
W przypadku półprzewodnika sytuacja jest odwrotna. Jednak rezystancja półprzewodnika spada około dziesięciokrotnie.
Wykonane pomiary odpowiadają wartością podanym w tablicach oraz literaturze.
6
Wyszukiwarka