Rama dwukrotnie statycznie niewyznaczalna

Temat zadania: rysujemy całą ramę ze wszystkimi obciążeniami.

1. Ramę statycznie niewyznaczalną możemy rozwiązać na dwa sposoby:

I. Rozwiązywanie bezpośrednio ze wszystkimi obciążeniami jednocześnie;

II. Z zasady superpozycji - rozwiązujemy wykresy sił przekrojowych osobno dla każdego pojedynczego obciążenia, a następnie sumujemy wszystkie wykresy.

Będziemy postępować zgodnie ze sposobem II.

W tym celu przyjmujemy układ podstawowy metody sił (U.P.M.S.) - dla wszystkich rodzajów obciążeń jednakowy:

Aby ułatwic rozwiązywanie zadania, obciążenie całkowite rozkładamy na jak najprostsze. W tym przypadku rozłożyliśmy je na 5 zadań.

Zadanie 1 i 2:

W rozwiązaniu tego zadania warto również wykorzystac zasadę superpozycji rozwiązując dwa, jeszcze prostsze zadania.

Zadanie 1: Zadanie 2:

Zadanie 3:

Zadanie 4:

Zadanie 5:

Wykonanie tematu nr 1:

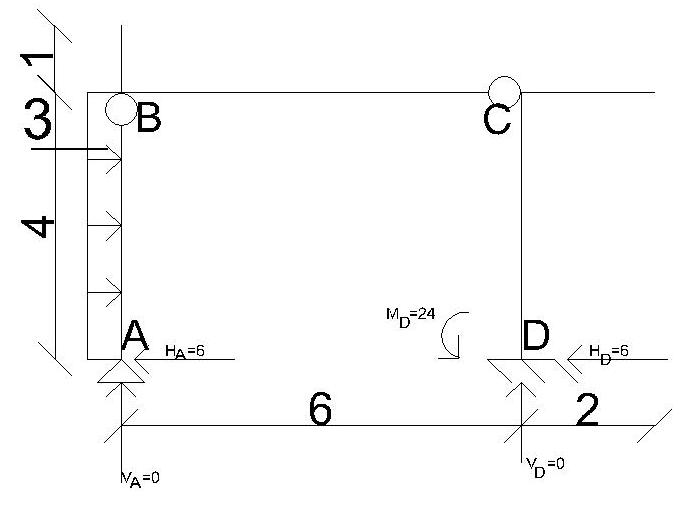
ΣM_B^A-B= 0

3*4* ½ *4- 4H_A=0

4H_A= 24

H_A= 6 kN

ΣM_C^A-B-C= 0

-6*4 + 3*4* ½ *4- 6V_A= 0

-24 +24= 6V_A

V_A= 0

ΣY= 0 → V_D= 0

ΣX= 0 →3*4 -6 -H_D=0

H_D= 6 kN

ΣM_D= 0

-3*4* ½ *4 + M_D= 0

M_D= 24 kNm

M_P

Wykresy od hiperstatycznych X₁ i X₂ są następujące:

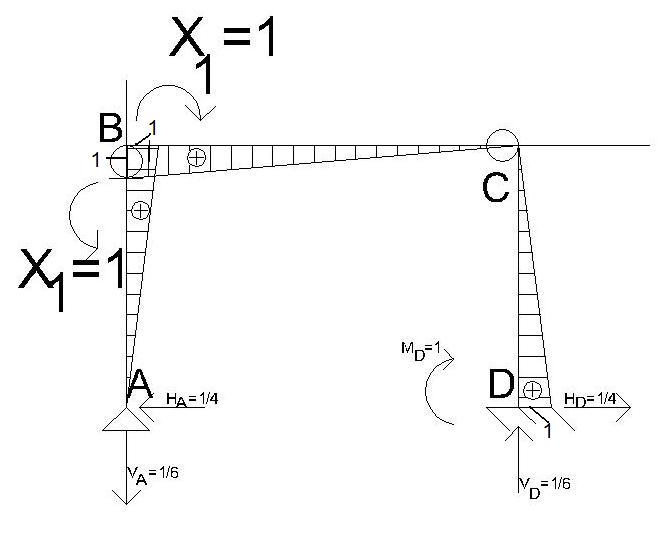
M₁ X1=1

ΣM_B^A-B= 0

4H_A- 1= 0

H_A= ¼

ΣM_C^A-B-C= 0

-¼ *4 -1+ 1 +6V_A=0

6V_A= 1

V_A= 1/6

ΣM_D= 0

1/6 *6 +1 - 1 -M_D= 0

M_D= 1

ΣX= 0 → H_D= ¼

ΣY= 0 → V_D= 1/6

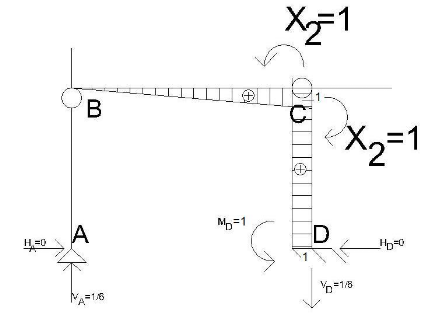
M₂ X2=1

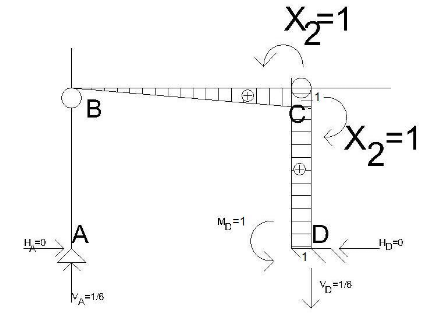
ΣM_B^A-B=0 → H_A= 0

ΣM_C^A-B-C = 0

-6V_A+ 1= 0

V_A= 1/6

ΣX= 0 → H_D= 0

ΣY= 0 → V_D= 1/6

ΣM_D=0

-1/6*6 +1- 1+ M_D= 0

M_D= 1

Wyznaczanie wartości hiperstatycznych X1 i X2 z warunku:

δ₁₁* X1+ δ₁₂* X2+ δ_1P= 0

δ₂₁* X2+ δ₂₂* X2+ δ_2P= 0

δ₁₂= δ₂₁

Wyliczanie δ₁₁, δ₁₂, δ_1P, δ₂₂, δ_2P za pomocą całkowania graficznego:

δ₁₁₌

= 1/EJ *[ ½* 4* 1* 2/3* 1+ ½* 1* 6* 2/3* 1+ ½* 4* 1* 2/3* 1] = 14/3EJ

δ₂₂₌

=1/EJ*[ ½* 1* 6* 2/3* 1+ 1* 4* 1]= 6/EJ

δ₁₂₌

= 1/EJ* [ ½* 6* 1* 1/3* 1 +(- ½* 1* 4* 1)]= - 1/EJ

δ_1P=

=1/EJ* [2/3* 4* 6 * ½* 1+ ½* 4* 24 * 2/3 *(-1)]= -24/EJ

δ_2P=

= 1/EJ* [ ½*4* 24* 1]= 48/EJ

δ₁₁=14/3EJ

δ₁₂ =δ₂₁= -1/EJ

δ₂₂= 6/EJ

δ_1P= -24/EJ

δ_2P= 48/EJ

Wyznaczanie wartości X1 i X2:

(14/3EJ)*X1- (1/EJ) X2- 24/EJ= 0 /*EJ

(-1/EJ)* X1+ (6/EJ)* X2+ 48/EJ= 0 /*EJ

(14/3)*X1- X2- 24= 0

-X1+ 6*X2+ 48= 0

X2= (14/3)*X1- 24

-X1+ 6*[(14/3)*X1- 24]+ 48= 0

-X1+ 28*X1- 144+ 48= 0

27*X1= 96

X1= 3,55556

X2= (14/3)*3,5556- 24

X2= -15,7037

Rysujemy wykresy M1 * X1 oraz M2 * X2

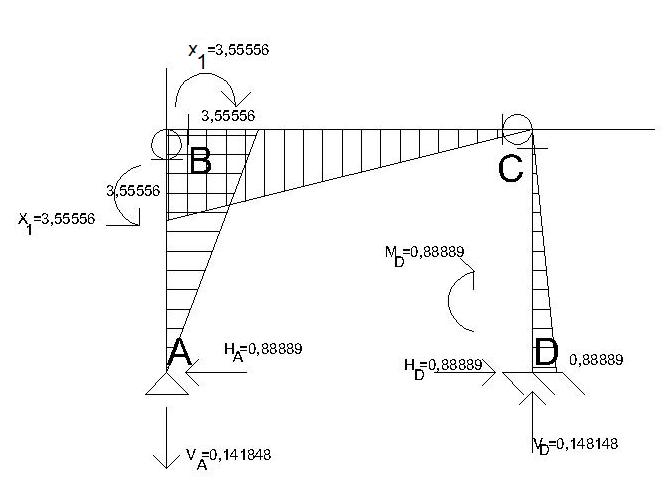
M1* X1=

ΣM_B^A-B= 0

4*H_A- 3,55556= 0

H_A= 0,88889 kN

ΣM_C^A-B-C= 0

0,88889*4- 6*V_A=0

V_A= 0,148148 kN

ΣX= 0→

H_D= 0,88889 kN

ΣY= 0 →

V_D= 0,148148 kN

ΣM_D= 0

0,148148* 6 -M_D= 0

M_D= 0,88889 kNm

M2* X2

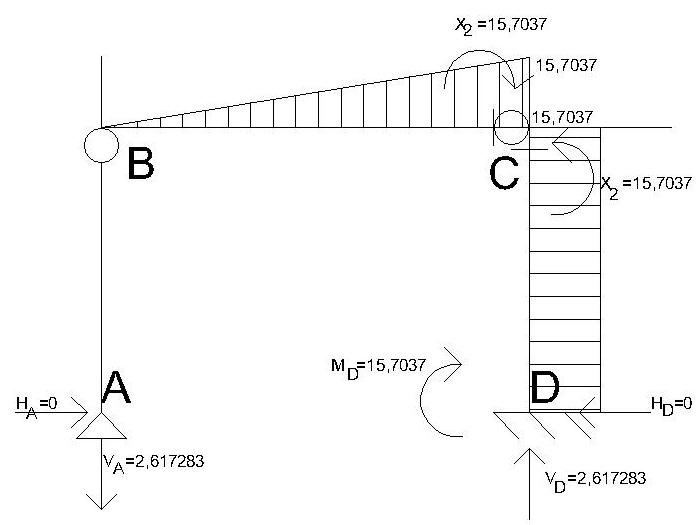
ΣM_A^A-B= 0 → H_A= 0

ΣM_C^A-B-C= 0

6*V_A- 15,7037= 0

V_A= 2,617283 kN

ΣX= 0 → H_D= 0

ΣY= 0 →

V_D= 2,617283 kN

ΣM_D= 0

6* 2,617283 - M_D= 0

M_D= 15,7037 kNm

Wykres momentów zginających MSN dla konstrukcji statycznie niewyznaczalnej otrzymamy dodając wszystkie wykresy momentów: M_P, M1* X1 oraz M2* X2:

M^SN= M1X1+ M2X2+ M_P

M_A= 0

M_B= 0 +0 +3,55556= 3,55556 kNm

M_1/2AB= 0+ ½* 3,55556 + 6= 7,77778 kNm

M_C= 0 - 15,7037+ 0= -15,7037 kNm

M_D= -0,88889 - 15,7037 + 24= 7,40741 kNm

M_max(AB)= 6,88889* 2,2963- 3*(2,2963)²/2= 7,90974 kNm

Sumowanie reakcji w podporach z wszystkich ram:

V_A= -0,148148 -2,617283 +0= -2,765431 kN

H_A= -0,88889+ 0 -6= -6,88889 kN

V_D= 0,148148+ 2,617283+ 0= 2,765431 kN

H_D= 0,88889+ 0- 6= -5,11111 kN

M_D= -0,88889- 15,7037+ 24= 7,40741 kNm

Wykresy sił przekrojowych Q i N:

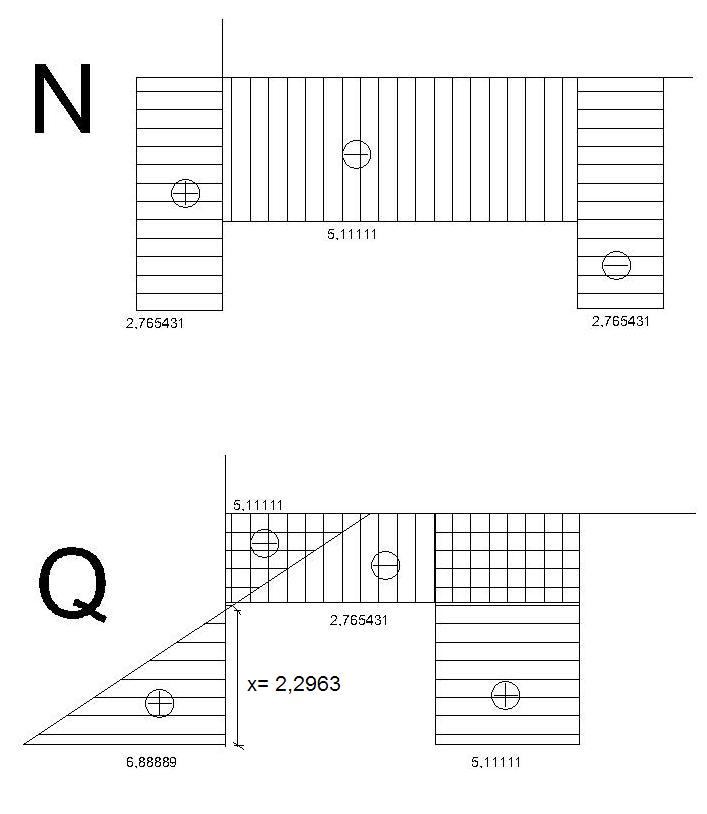
X= 4* 6,8889/12

X= 2,2963

Sprawdzenie: Równowaga w węźle C:

ΣM= 15,7037- 15,7037= 0

ΣX= -5,11111 + 5,11111= 0

ΣY= 2,765431- 2,765431= 0

Budownictwo/Stacjonarne/Rok II

---