Nr ćwicz. 201	Data: 30.10.98	Michał Marczak	Wydział Elektryczny	Semestr I	Grupa T3
Prowadzący: H. Manikowski					Przygotowanie:	Wykonanie:	Ocena ostat. :

Temat : Wyznaczanie zależności przewodnictwa od temperatury dla półprzewodników i przewodników .

Wstęp teoretyczny:

Prawo Ohma w najogólniejszej postaci stwierdza, że gęstość prądu w dowolnym miejscu materiału przewodzącego jest wprost proporcjonalna do natężenia pola elektrycznego:

gdzie j - gęstość prądu ,

E - natężenie pola elektrycznego ,

- przewodnictwo elektryczne .

Przewodnictwo elektryczne określone jest wzorem :

n , p - koncentracje nośników ,

n , p - ruchliwość nośników .

Ponieważ koncentracja i ruchliwość zależą od temperatury i rodzaju materiału, więc przewodnictwo elektryczne także zależy od tych czynników.

O zależności temperaturowej przewodnictwa w metalach decyduje tylko zmniejszanie się ruchliwości wraz ze wzrostem temperatury ( koncentracja nośników - elektronów - jest bardzo duża i nie zależy od temperatury ). Zależność temperaturową wyraża się poprzez opór (R1/ ) :

R0 - opór w temperaturze T0 ,

- średni współczynnik temperaturowy .

W półprzewodnikach decydujący wpływ na przewodnictwo ma koncentracja nośników. W przypadku półprzewodników samoistnych koncentracja elektronów i dziur jest taka sama i wynosi :

,

Eg - szerokość pasma zabronionego .

Natomiast w półprzewodnikach domieszkowych koncentracje określone są poprzez poziomy energetyczne (zależnie od typu półprzewodnika ) Ed - donorowy , Ea - akceptorowy , oraz poprzez temperaturę :

.

Uwzględniając powyższe równania otrzymujemy wzór na temperaturową zależność przewodnictwa dla półprzewodników :

,

Edom jest jedną z wielkości Ed lub Ea zależnie od typu półprzewodnika .

W odpowiednio niskich temperaturach można zaniedbać w powyższym wzorze pierwszy składnik , natomiast w wysokich temperaturach ( po nasyceniu poziomów domieszkowych ) można zaniedbać składnik drugi . Odpowiednio dla tych dwóch przypadków wzór przyjmie postać :

.

Logarytmując jeden z powyższych wzorów otrzymamy zależność :

Z wykresu tej zależności wygodnie jest odczytać zależność przewodnictwa od temperatury :

Zasada pomiaru:

Pomiarów oporu półprzewodnika i przewodnika dokonuje się w różnych temperaturach. Badane materiały umieszczone są w ultratermostacie , a ich opory mierzy się przy pomocy mostka Wheatstone'a .

Pomiary:

Przybliżone wartości oporów : (w tempetaturze pokojowej ok. 28°C)

Rprz = 110

Rpół = 8700

Lp	Temperatura [°C ]	Opór przewodnika []	Temperatura [°C ]	Opór półprzewodnika []
1	35	113,9	35	6210
2	40	114,7	40	5880
3	45	116,9	45	5200
4	50	119,7	50	4790
5	55	121,6	55	3850
6	60	122,3	60	3740

Analiza pomiarów:

Błąd pomiaru rezystancji mostkiem Wheatstone'a : R=0.1

Błąd pomiaru temperatury : T=1C

Dla przewodnika:

Lp	T [C]	1/T [1/C]	R []	ln(1/R)
1	28	0.0357	110	- 4,70048
2	35	0.02857	113,9	- 4,73532
3	40	0.025	114,7	- 4,74232
4	45	0.0222	116,9	- 4,76132
5	50	0.02	119,7	- 4,78499
6	55	0.0182	121,6	- 4,80074
7	60	0.0167	122,3	- 4,80648

Dla półprzewodnika:

Lp	T [C]	1/T [1/C]	R []	ln(1/R)
1	28	0.0357	8700	- 9,07108
2	35	0.02857	6210	- 8,73392
3	40	0.025	5880	- 8,67931
4	45	0.0222	5200	- 8,55641
5	50	0.02	4790	- 8,47429
6	55	0.0182	3850	- 8,25583
7	60	0.0167	3740	- 8,22684

dla półprzewodnika zależność lh(1/R) oraz 1/T wygląda następująco:

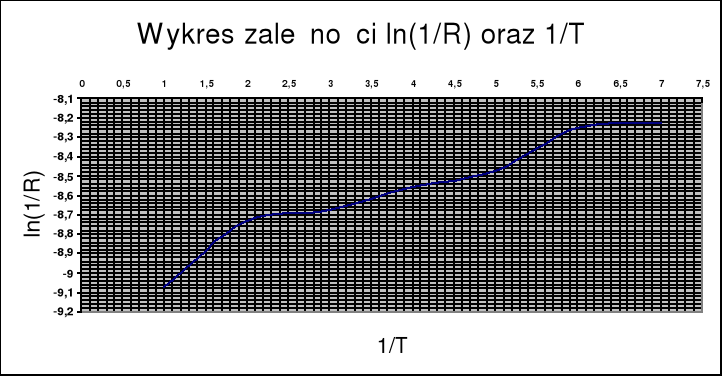
Przy pomocy programu komputerowego obliczamy współczynnik nachylenia prostej ln(1/R) = f(1/T) (metoda regresji):

a= -71.4027

a= -7.8205 .

Poziom domieszkowy będzie zatem równy :

Błąd wyznaczenia poziomu domieszkowego :

Wynik:

E=(0.01230.0014)eV

---