Zadania do ćwiczeń

1. Popyt i podaż

1. Przeanalizuj rynek herbaty. Każdą z poniższych zmian przedstaw graficznie na osobnym wykresie i podaj interpretację zaistniałej na rynku sytuacji (analizę rozpocznij od narysowania pierwotnej krzywej popytu i podaży).

1. Panujące upały spowodowały liczne pożary, które zniszczyły większą część zbiorów herbaty.

2. Opublikowano wyniki badań, które stwierdziły szkodliwe właściwości herbaty.

3. Dogodne warunki klimatyczne spowodowały obfite zbiory herbaty. Producenci prowadzą intensywną kampanię reklamową.

2. Co stanie z krzywą podaży ropy naftowej, jeżeli jakiś nowy wynalazek umożliwi tanią eksploatację szybów ropy z porzuconych już otworów wiertniczych? Pokaż graficznie jak zmieni się punkt równowagi rynkowej.

3. Co stałoby się z krzywą podaży obrazów Pietera Brueghela starszego, jeżeli odnalazłaby się reszta jego obrazów z cyklu 12 miesięcy? Pokaż graficznie jak zmieniłby się punkt równowagi rynkowej.

4. Co stałoby się z krzywą popytu na insulinę , jeżeli w wyniku zmian cywilizacyjnych ludzie zaczęliby częściej chorować na cukrzycę. Pokaż graficznie jak zmieniłby się punkt równowagi rynkowej.

5. Funkcja popytu na jelenie ma postać D(p)= 40-p, natomiast funkcja podaży jeleni dana jest wzorem S(p)=10+p.

1. Podaj cenę i ilość równowagi na rynku jeleni.

2. Dyrekcja lasów państwowych podejmuje decyzję o ograniczeniu hodowli jeleni na sprzedaż do 20 sztuk. Przy jakiej cenie popyt wyniesie 20 jeleni? Ile jeleni dostarczą producenci po tej cenie? Przy jakiej cenie producenci dostarczą tylko 20 jeleni?

3. Przedstaw graficznie i omów wpływ na równowagę rynku jeleni wzrostu dochodów odbiorców jeleni oraz niespodziewanie wysokiej liczby urodzeń wśród jeleni.

6. Odwrotna funkcja popytu na pewne dobro wynosi 5p=150-Q_D natomiast funkcja podaży dana jest wzorem Qs = 5p.

1. Oblicz ilość oraz cenę równowagi na rynku tego dobra.

2. W ramach szukania dodatkowych dochodów do budżetu państwo nałożyło na to dobro podatek w wysokości 100%. Ile teraz wynoszą ceny i ilość równowagi.

3. Gdyby w ramach polityki ochrony producentów danego dobra państwo zamiast podatku wprowadziło cenę minimalną na dane dobro w wysokości 20 zł ile wynosiłaby nadwyżka podaży nad popytem?

7. Na rynku dóbr A i B jest równowaga. Na obydwu rynkach występuje identyczna krzywa podaży. W punkcie równowagi cenowa elastyczność popytu dobra A jest znacząco niższa niż dobra B. W wyniku ingerencji rządu na każdą sprzedaną sztukę A i B zostaje nałożona identyczna kwota podatku pośredniego t.

1. Wyjaśnij, jak relatywnie zmieni się cena i ilość kupowanych dóbr A i B. Wykorzystaj ilustrację graficzną (uwaga: uzupełnij rysunek o brakującą krzywą popytu).

2. Ile musiałaby wynosić cenowa elastyczność popytu, aby o całą kwotę podatku wzrosła cena dobra A?

3. Ile musiałaby wynosić cenowa elastyczność popytu, aby cena dobra B w ogóle się nie zmieniła?

8. Załóżmy, że politycy planują nałożenie na każda sprzedaną sztukę kosmetyków "Cudowny Krem" podatku w wysokości 20PLN. Wyjaśnij, czy cena płacona przez konsumentów wzrośnie o mniej czy tez więcej niż 20PLN, a może wzrośnie dokładnie o 20PLN. Wykorzystaj ilustracje graficzną.

9. Popyt na kawior astrachański dany jest wzorem D(p_D)= 120 - 4p_D (p_D - cena płacona przez konsumenta), natomiast funkcja podaży kawioru dana jest wzorem S(p_S)=2p_S - 30 (p_S - cena otrzymywana przez producenta).

1. Jaka jest cena i ilość równowagi na rynku kawioru astrachańskiego?

2. W wyniku choroby jesiotrów krzywa podaży przesunęła się do S(p_S)=2p_S - 60. Podaj nową cenę i ilość równowagi.

3. Rząd rosyjski podejmuje akcję pomocy producentom i konsumentom kawioru i dopłaca do każdej puszki tego produktu dotację w wysokości 15 rubli. Podaj nowe ceny i ilość równowagi.

10. Funkcja popytu na perfumy Flower Kenzo dana jest wzorem D(p_D)= 100/p_D (p_D - cena płacona przez konsumenta), natomiast funkcja podaży to S(p_S)=p_S (p_S - cena otrzymywana przez producenta).

1. Jaka jest cena i ilość równowagi na rynku perfum Flower?

2. Na perfumy został nałożony podatek od wartości w wysokości 300% tak, że cena płacona przez konsumentów jest 4 razy wyższa od ceny otrzymywanej przez dostawców. Jakie są obecnie ceny i ilość równowagi?

11. Funkcja popytu na kanapki z rybą ma postać D(p_D)= -2p_D + 70 (p_D - cena płacona przez konsumenta), natomiast funkcja podaży dana jest wzorem S(p_S)=5p_S (p_S - cena otrzymywana przez producenta).

1. Podaj cenę i ilość równowagi na rynku kanapek z rybą .

2. Załóżmy, że z powodu problemów z dostawą niezbędnych składników do przygotowania kanapek z rybą ilość kanapek dostępnych na rynku została ograniczona do 30 sztuk. Przy jakiej cenie popyt wynosiłby 30 sztuk? Ile kanapek producenci byliby skłonni dostarczyć na rynek przy tej cenie? Przy jakiej cenie producenci dostarczą tylko 30 kanapek?

3. Oblicz, ile kanapek z rybą będzie dostarczonych na rynek po wprowadzeniu dotacji dla producentów w wysokości 7 zł do każdej kanapki.

4. Przedstaw graficznie i omów wpływ na równowagę rynku kanapek z rybą spadku dochodów smakoszy kanapek z rybą oraz poważnego uszkodzenia w czasie sztormu kutrów łowiących ryby.

12. Funkcja popytu na czerwone wino wynosi D(p_D)=1000 - 10p_D (p_D - cena płacona przez konsumenta). Funkcja podaży ma postać S(p_S)= 100 + 20p_S (p_S - cena otrzymywana przez producenta). Za każdą sprzedaną butelkę czerwonego wina rząd pobiera podatek równy połowie ceny płaconej przez konsumentów. Znajdź cenę i ilość równowagi na rynku czerwonego wina.

13. W okresie t₁ cena Czarodziejskiej Góry Tomasza Manna w antykwariacie wynosiła 60zł za 2 tomy. W okresie t₂ wydawnictwo Dolnośląskie wprowadziło na rynek nowe wydanie Czarodziejskiej Góry w cenie 40 zł za 2 tomy. Co się stanie w okresie t₃ z ceną Czarodziejskiej Góry na rynku antykwarycznym? Przedstaw ten przypadek na wykresie. Zaznacz odpowiednie przesunięcia funkcji popytu i\lub podaży.

14. Jerzy Nowosielski i Jerzy Wolff to znani polscy malarze XX wieku. Całkowita podaż obrazów Wolffa wynosi 100 sztuk natomiast Nowosielskiego 150. Popyt na dzieła każdego z tych malarzy zależy od ceny jego obrazów oraz od ceny dzieł drugiego malarza. Funkcja popytu na obrazy Wolffa dana jest wzorem D_W(p)=200 - 4p_W - 2p_N; na obrazy Nowosielskiego D_N(p) = 300 - 3p_N - p_W; gdzie p_{W i} p_N to odpowiednio ceny obrazów Wolffa i Nowosielskiego.

1. Znajdź ceny obrazów Wolffa i Nowosielskiego w stanie równowagi.

2. Na rysunku zaznacz wszystkie kombinacje cen dzieł Nowosielskiego i Wolffa, dla których podaż obrazów Nowosielskiego jest równa popytowi na nie.

2. Elastyczności

1. Dobra A i B mają mieszaną cenową elastyczność popytu równą 1,2.

1. wyjaśnij czy są to dobra substytucyjne, czy komplementarne.

2. O ile wzrośnie popyt na dobro B jeśli cena dobra A wzrasta z 20 zł do 25 zł za kg?

2. Wielkość popytu na dobro X przy cenie 10 zł za sztukę wynosiła 200 sztuk. W wyniku wzrostu ceny wielkość popytu spadła o 40 sztuk. Oblicz jak zmieniła się cena dobra X i odpowiedz czy zmieniły całkowite wydatki na dobro X jeśli elastyczność cenowa popytu wynosi E_p = 2.

3. Przy cenie 4 zł za 1 kg winogron , całkowity popyt na nie wynosi 100 kg dziennie.

1. Ile wyniesie wielkość popytu, gdy ich cena wzrośnie do 5 zł za 1 kg jeśli wiadomo, że elastyczność cenowa popytu na winogrona jest równa 2?

2. Ile wynosi przyrost utargu całkowitego?

4. Załóżmy, że cena cukru wzrosła z 10 zł do 15 zł za kilogram. Spowodowało to spadek popytu z 50 kg do 40 kg.

1. Ile wynosi przyrost utargu całkowitego?

2. Jaka jest cenowa elastyczność popytu?

5. Producent słodyczy podniósł cenę czekolady z 10PLN do 20PLN za kilogram. Spowodowało to spadek ilości popytu ze 100 kg do 80 kg. Oblicz cenową elastyczność popytu. Ile wynosi przyrost utargu całkowitego?

6. Kiedy winogrona kosztują 4PLN za kg, wtedy całkowity popyt na nie wynosi w Warszawie 100 kg dziennie. Jeśli ich cenowa elastyczność popytu wynosi e = 1,5, to ile wyniesie wielkość popytu, gdy ich cena wzrośnie do 6PLN za kg. Ile wynosi przyrost utargu całkowitego?

7. Tabela zawiera ilości trzech dóbr (A, B, C) zakupionych przez konsumentów w ciągu 2 lat. Ceny tych dóbr w ciągu tego okresu nie zmieniły się, ale zmienił się dochód konsumentów.

X	Dobro A	Dobro B	Dobro C	Dochód
Rok I	50	60	100	50 000
Rok II	60	30	200	80 000

1. Jaka jest elastyczność dochodowa popytu (łukowa) na te dobra?

2. Określ do jakiej kategorii należy każde z tych dóbr.

8. Popyt na czekoladę wynosi 1000 tabliczek dziennie. Cena pierników z nadzieniem wynosi 5 zł. W wyniku wzrostu ceny pierników o 100%, popyt na czekoladę wzrósł o 20%.

1. Oblicz elastyczność mieszaną popytu.

2. Określ, jaki charakter ma więź w jakiej pozostają czekolada i pierniki z nadzieniem.

9. Popytu na rosyjskie budziki jest opisany funkcją liniową. Elastyczności mieszana popytu wynosi 2,5. Jak się zmieni popyt na rosyjskie budziki jeśli cena takich samych zegarków produkcji chińskiej wzrośnie o 6%?

10. W wyniku obniżenia ceny biletu do ZOO z 9zł do 6zł Warszawiacy zaczęli chętniej odwiedzać egzotyczne zwierzęta. Liczba odwiedzających ZOO tygodniowo wzrosła z 5000 do 6000 osób. Oblicz wartość współczynnika elastyczności cenowej popytu na bilety do ZOO.

1. Dokonaj interpretacji ekonomicznej otrzymanego wyniku.

2. Określ wpływ obniżenia ceny na przychody całkowite ZOO.

3. Co doradziłbyś dyrektorowi ekonomicznemu tej instytucji?

11. jeśli popyt na pewien produkt jest określony jako elastyczny względem ceny, to:

1. wzrost ceny spowoduje zmniejszenie sprzedanej ilości i spadek utargu

2. wzrost ceny spowoduje zmniejszenie sprzedanej ilości, ale utarg wzrośnie

3. spadek ceny spowoduje zwiększenie sprzedanej ilości, ale utarg zmaleje

4. spadek ceny spowoduje zwiększenie sprzedanej ilości i zwiększenie utargu

5. żadna odpowiedź nie jest prawidłowa.

12. Jeśli dochodowa elastyczność popytu na dane dobro wynosi 0,6 , to popyt zmienia się:

1. w odwrotnym kierunku niż dochód;

2. w takim samym kierunku co dochód, lecz w mniejszym stopniu;

3. w takim samym kierunku co dochód i w tym samym stopniu;

4. w takim samym kierunku co dochód, ale w większym stopniu .

13. Dobro konsumpcyjne należy do dóbr niższego rzędu, gdy elastyczność:

1. dochodowa popytu wynosi 0,5;

2. cenowa popytu wynosi -1,3;

3. cenowa mieszana popytu wynosi -0,7;

4. dochodowa popytu wynosi 1,3;

5. cenowa mieszana popytu wynosi 0,1.

14. Zinterpretuj następujące wskaźniki:

1. - prosta elastyczność cenowa popytu I+0,3I,

2. - elastyczność mieszana popytu -0,2,

3. - elastyczność cenowa podaży +1,2,

4. - elastyczność dochodowa popytu +0,7

(należy podać kierunek i natężenie zmian popytu lub podaży oraz określić rodzaj dobra).

15. Tablica przedstawia dochodową elastyczność popytu na 3 dobra.

1. Objaśnij jak zmienią się krzywe popytu na każde z tych dóbr pod wpływem spadku dochodu.

2. Jakie to są dobra?

3. Podaj przykłady takich dóbr.

Dobro	Dochodowa elastyczność popytu
A B C	1,7 -0,8 0

16. Popyt Tomasza na kanapki określony jest wzorem
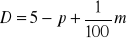
    ; gdzie p jest ceną kanapki i wynosi 3zł natomiast m oznacza miesięczne kieszonkowe Tomasza i wynosi 100zł. Wyznacz elastyczność cenową popytu oraz elastyczność dochodową popytu. Jakim dobrem są dla Tomasza kanapki.

17. Funkcja popytu Kazi na wodę ma postać x = 7 - 2p (p - cena). Wiemy, że funkcja popytu Ziuty na wodę ma także postać liniową; przy cenie p = 1 popyt Ziuty wynosi 4, zaś elastyczność cenowa popytu Ziuty ε = 0.25. Ile wyniesie łączny popyt obu pań na wodę, gdy cena p = 4?

18. Funkcja popytu Ani na perfumy 5th Avenue ma postać x = 2 + 2y (y - dochód, x - popyt). Wiemy, że funkcja popytu Magdy na te perfumy ma także postać liniową; przy dochodzie Magdy y = 4 jej popyt wynosi 6, zaś elastyczność dochodowa popytu Magdy E_M = 2/3. Ile wyniesie łączny popyt obu pań na perfumy, gdy ich dochody będą równe i wyniosą y = 7? Skomentuj różnicę w wartościach elastyczności cenowych popytu obu pań na te perfumy: w przypadku Ani elastyczność ta wynosi I+1,3I, w przypadku Magdy I-1,3I.

19. Funkcja popytu na harfy wyrażona jest wzorem p=10-q. Przy jakiej cenie przychód realizowany ze sprzedaży harf będzie maksymalny? Ile harf można sprzedać po tej cenie?

20. Wzór na funkcję odwrotną do funkcji popytu na banany przedstawia się następująco: p_D=18 - 3q_D, a odwrotna funkcję podaży dana jest wzorem: p_S=6 + q_S.

1. Podaj cenę i ilość równowagi.

2. Jaka jest nowa ilość równowagi jeśli dostawcy otrzymują subsydia w wysokości 2zł? Jakie są ceny dostawców i odbiorców?

3. Co się stanie z wielkością zapotrzebowania na jabłka w konsekwencji wprowadzenia subsydiów dla producentów bananów jeśli wiadomo, że elastyczność mieszana między jabłkami i bananami wynosi 0,5.

3. Konsument

1. Popyt konsumenta na jogurt malinowy wynosił 100 litrów rocznie, a na krakersy wynosił 50 opakowań rocznie, kiedy ceny tych dóbr wynosiły odpowiednio: p_j = 2 zł i p_k = 4 zł. Załóżmy, że ceny wzrosły do: p_j = 3 zł i p_k = 5 zł. O ile musiał wzrosnąć dochód konsumenta, aby mógł on utrzymać swoją konsumpcję na nie zmienionym poziomie?

2. Jeśli początkowo dochód konsumenta wynosił 2000 zł, natomiast ceny dóbr A i B wynosiły odpowiednio p_A = 20 zł i p_B = 40 zł, a następnie dochód wynosił 3000 zł, p_A = 30 zł i p_B = 60 zł, to jak zmieniła położenie linia budżetu?

3. Pani Basia wydaje cały swój dochód dzienny na ptasie mleczko i gumy do żucia, przy czym może pozwolić sobie na zakup 20 ptasich mleczek (M) i 40 gum do żucia (G) dziennie. Mogłaby także kupić za cały swój dochód 30 ptasich mleczek i 20 gum do żucia dziennie, jeśli cena ptasiego mleczka wynosi 1 zł. Ile wynosi dzienny dochód pani Basi?

4. Linia budżetu dla dóbr A i B dana jest wzorem: 5A + B = 20. Konsument kupuje 2 sztuki dobra A i 10 sztuk dobra B. Z ilu sztuk dobra A konsument musi zrezygnować, aby zwiększyć zakupy dobra B o 5 sztuk?

5. W pewnym kraju istnieją tylko 2 dobra: kasza i miód. Kasza kosztuje 2 dukaty za kilogram, a miód 6 dukatów za garniec.

1. Napisz równanie budżetowe obywatela tego kraju Mieszka, który dysponuje dochodem w wysokości 360 dukatów.

2. Mieszko jest urzędnikiem państwowym w wyniku zmiany władzy jego dochody rosną dwukrotnie. Nie jest to niestety jedyna zmiana, jednocześnie Mieszko spostrzega, że cena kaszy wzrosła również dwukrotnie natomiast cena miodu wzrosły trzykrotnie. Napisz nowe równanie budżetowe Mieszka.

3. Przedstaw graficznie ograniczenie budżetowe Mieszka. Narysuj jak wyglądałyby krzywe preferencji Mieszka jeżeli wiadomo, że zdecydowanie woli on miód niż kaszę.

6. Konsument poszukuje optymalnego koszyka składającego się z dwóch dóbr α i β, gdzie α to dobro Giffena, zaś β to dobro normalne. Zakładając, że preferencje konsumenta, jego dochód oraz cena dobra β nie ulegają zmianie, pokaż jak zmieni się punkt równowagi konsumenta w przypadku wzrostu ceny dobra α. Zaznacz ścieżkę zmiany cen. Wyznacz graficznie krzywą indywidualnego popytu na dobro α.

7. Koszyk dóbr wybierany przez Jasia składa się z klocków lego i książeczek. Wyjaśnij jak zmieni się popyt Jasia na klocki lego jeśli wzrośnie cena książeczek przy założeniu, że dobra te są substytutami. Przedstaw sytuację na wykresie i zaznacz efekty dochodowy i substytucyjny wzrostu ceny klocków lego na popyt Jasia na książeczki.

8. Małgosia konsumuje 2 dobra: domino i cukierki. Najbardziej jest zadowolona kiedy jednocześnie gra w domino i je cukierki. Wyjaśnij jak zmieni się popyt Małgosi na domino jeśli wzrośnie cena cukierków. Przedstaw sytuację na wykresie i zaznacz efekty dochodowy i substytucyjny wzrostu ceny cukierków na popyt Małgosi na domino.

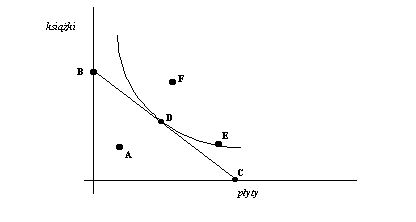
9. Paweł zastanawia się, jak podzielić pieniądze przeznaczone na zakup płyt i książek. Poniższy rysunek ilustruje linię budżetową oraz krzywą obojętności.

Przyporządkuj oznaczone na wykresie punkty odpowiednim zadaniom:

- wybór zapewniający Pawłowi maksymalną osiągalną użyteczność ............

- w koszyku Pawła znajdują się tylko płyty .............

- Paweł nie wydaje pełnej kwoty swojego dochodu ............

- kombinacja o takiej samej użyteczności jak D, ale nieosiągalna dla Pawła ...........

- Paweł całkowicie rezygnuje z płyt ..............

- kombinacja lepsza niż D, ale nieosiągalna dla Pawła ...............

10. 
    Konsument poszukuje optymalnego koszyka składającego się z dwóch dóbr α i β, gdzie α to dobro niższego rzędu, zaś β to dobro normalne. Zakładając, że preferencje konsumenta, jego dochód oraz cena dobra β nie ulegają zmianie, pokaż jak zmieni się punkt równowagi konsumenta w przypadku wzrostu ceny dobra α. Zaznacz ścieżkę zmiany cen. Wyznacz graficznie krzywą Engla dla dobra α.

11. Wykaż, czy następujące twierdzenie jest prawdziwe, czy też fałszywe: „Dobro niższego rzędu nie musi być dobrem Giffena. Natomiast każde dobro Giffena jest dobrem niższego rzędu”.

12. Co to jest równowaga konsumenta? Pokaż graficznie stan równowagi. Kiedy optymalne rozwiązanie przyjmuje postać rozwiązania brzegowego?

13. Pojęcie krzywej obojętności. Wyjaśnij i uzasadnij kiedy krzywe obojętności mają kształt wklęsły, a kiedy wypukły?

14. Przedstaw graficznie mapę preferencji konsumenta w przypadku gdy konsument wybiera spośród dwóch dóbr doskonale substytucyjnych. Uzasadnij swój wybór.

15. Konsument dysponuje dochodem M = 16 zł, cena dobra A wynosi 2 zł, a cena dobra B wynosi 1 zł. Która z następujących kombinacji dóbr leży na linii budżetu konsumenta:

1. 6A i 4B,

2. 5A i 6B,

3. 7A i 3B,

4. 6A i 5B.

16. Jeśli ilości dobra A mierzymy na osi odciętych, a dobra B na osi rzędnych, to wzrost ceny dobra A spowoduje:

1. równoległe przesunięcie w górę linii budżetu,

2. przesunięcie w lewo punktu styczności linii budżetu z osią OX,

3. równoległe przesunięcie w dół linii budżetu,

4. zmniejszenie kąta nachylenia linii budżetu.

17. Krzywa obojętności przedstawia różne kombinacje dóbr, które:

1. dają konsumentowi taką samą użyteczność krańcową,

2. dają konsumentowi taką samą użyteczność całkowitą,

3. dają konsumentowi taką samą użyteczność przeciętną,

4. mają te same ceny.

18. Linia ograniczenia budżetowego jest zbiorem koszyków dóbr, które:

1. mają taką samą użyteczność krańcową,

2. przy danych cenach dóbr i dochodzie konsumenta zawierają minimalną dostępną ilość jednego dobra przy danej ilości drugiego dobra,

3. kosztują tyle ile wynosi dochód konsumenta,

4. nie są dostępne dla konsumenta przy danych cenach i danym dochodzie.

19. Równoległe przesunięcie linii ograniczenia budżetowego nastąpi pod wpływem:

1. zmniejszenia się dochodu konsumenta (ceny pozostają stałe),

2. zmiany preferencji konsumenta,

3. zmiany ceny jednego dobra,

4. zmiany krańcowej stopy substytucji obu dóbr.

20. Ścieżka wzrostu dochodu jest:

1. zbiorem punktów równowagi konsumenta, odpowiadających różnym relacjom cen kupowanych przez niego dóbr,

2. zbiorem punktów równowagi konsumenta, odpowiadających różnym poziomom dochodu konsumenta,

3. zbiorem punktów równowagi konsumenta, powstających przy zmianach preferencji konsumenta,

4. żadna z powyższych odpowiedzi nie jest prawidłowa.

21. Tomasz dysponuje dochodem w wysokości 400 zł. Maksymalna ilość kanapek (K), którą mógłby kupić to 80 sztuk, zaś cena obiadu na stołówce (O) wynosi 10 zł. Wiadomo również, że w optimum krańcowa stopa substytucji MRS opisana jest wzorem O/K. Określ ile kanapek i obiadów K i O wybierze Tomasz biorąc pod uwagę swoje możliwości finansowe i dążąc jednocześnie do maksymalizacji użyteczności.

22. Ela otrzymuje od rodziców kieszonkowe w wysokości 80zł miesięcznie, które w całości przeznacza na zakup czekolady i Coca Coli. W ciągu miesiąca zjada 20 czekolad, które kupuje po 3zł za sztukę. Ile puszek Coca Coli kupuje Ela miesięcznie, jeśli wiadomo, że w punkcie równowagi, w którym maksymalizuje użyteczność z konsumpcji jest skłonna poświęcić 3 puszki Coca coli za jedną czekoladę.

23. Joanna wydaje cały swój dochód w wysokości 600zł miesięcznie na ostrygi i kiepskie wino musujące.

1. Ile kieliszków wina wypija Joanna jeśli jeden kieliszek tego trunku kosztuje 8 zł, a na porcję ostryg wydaje 20zł?

2. Ile kieliszków wina będzie konsumować Joanna jeżeli jego cena spadnie do 5 zł za kieliszek podczas gdy dochód Joanny i cena ostryg pozostanie bez zmian?

3. Jaka kwota dochodu musi być jej odebrana dla wyodrębnienia efektu dochodowego i substytucyjnego w ujęciu Hicksa?

4. Wskaż: całkowity efekt zmiany ceny, efekt dochodowy oraz efekt substytucyjny.

5. Jakim dobrem dla Joanny jest wino musujące?

4. Funkcja produkcji i próg rentowności

1. Firma produkująca telefony bezprzewodowe otrzymała zamówienie na dostarczenie 500 telefonów. Do wyprodukowania telefonu potrzebne są dwa czynniki wytwórcze praca i kapitał. Pokaż graficznie sposób wyboru optymalnej techniki wytworzenia 500 sztuk telefonów. Pokaż za pomocą izokwant korzyści skali w produkcji telefonów.

2. Firma produkująca pluszowe misie otrzymała zamówienie na dostarczenie 1000 misiów. Do wyprodukowania misia potrzebne są dwa czynniki wytwórcze praca i kapitał. Pokaż graficznie sposób wyboru optymalnej techniki wytworzenia 1000 sztuk misiów.

3. Mając daną krzywą produktu całkowitego przedsiębiorstwa jako funkcję jednej zmiennej L (praca), opisz charakter jej przebiegu dla różnych poziomów L oraz wyznacz graficznie funkcje produkcyjności przeciętnej i krańcowej (konieczne jest uzasadnienie przebiegu tych funkcji i ich punktów charakterystycznych).

4. Jeżeli produkcyjność przeciętna maleje, to:

1. produkcyjność krańcowa jest większa od produkcyjności przeciętnej,

2. produkcyjność krańcowa jest mniejsza od produkcyjności przeciętnej,

3. funkcja produkcji osiąga maksimum a produkcyjność krańcowa jest równa zero,

4. produkcyjność przeciętna jest równa produkcyjności krańcowej.

5. Zmniejszenie kosztów stałych nastąpi przez:

1. wzrost wielkości produkcji,

2. spadek wielkości produkcji,

3. wstrzymanie produkcji,

4. żadna z powyższych odpowiedzi nie jest dobra.

6. Zdefiniuj pojęcie progu rentowności firmy. Przy założeniu, że funkcja kosztów całkowitych przedsiębiorstwa konkurencyjnego dana jest jako: C = 2Q + 32 (Q - ilość sztuk produkcji), zaś cena wynosi 10 jednostek, wyznacz próg rentowności firmy. Czy próg rentowności zmieni się gdy funkcja kosztów przyjmie postać C = 2Q?

7. W gałęzi X są do dyspozycji dwie technologie wytwarzania. Technologia małej skali pozwala wytwarzać w jednym przedsiębiorstwie do 200 szt. rocznie, przy koszcie stałym FC = 1000 zł i jednostkowym koszcie zmiennym AVC = 1 zł/szt. Technologia dużej skali pozwala wytwarzać w jednym przedsiębiorstwie do 2000 szt. rocznie, przy koszcie stałym FC = 4000 zł i jednostkowym koszcie zmiennym AVC = 2 zł/szt. W obu technologiach koszty AVC = const.

a. oblicz dla każdej technologii próg rentowności wiedząc, że cena wynosi p = 9 zł/szt.

b. jaką technologię zaakceptuje rynek, jeśli łączny popyt rynkowy wynosi 600 szt./rok?

c. czy coś zmieni się, jeśli łączny popyt wyniósłby 1200 szt./rok?

8. Przedsiębiorstwo zabawek „Konik Garbusek” działa na rynku konkurencyjnym na którym cena zbytu wynosi 30 zł za sztukę. Wiemy, że koszty zmienne firmy są proporcjonalne do wielkości produkcji, jednostkowy koszt zmienny wynosi 6 zł, zaś całkowity koszt stały 120 zł.

a. Zdefiniuj pojęcia kosztu zmiennego i stałego (przykłady).

b. Przedstaw analitycznie funkcję kosztu całkowitego

c. Wylicz próg rentowności firmy

d. Ile wyniósłby próg rentowności gdyby całkowity koszt stały = 0?

9. Pewne przedsiębiorstwo doskonale konkurencyjne produkuje skarpetki. Funkcja przeciętnych kosztów stałych tego przedsiębiorstwa ma postać AFC= 600/Q, natomiast funkcja przeciętnych kosztów zmiennych jest dana wzorem AVC=2. Rynkowa cena pary skarpetek wynosi P=5zł. Oblicz próg rentowności tego przedsiębiorstwa.

10. Zdefiniuj pojęcie progu rentowności firmy. Przy założeniu, że funkcja kosztów jednostkowych przedsiębiorstwa konkurencyjnego dana jest jako: AC = 2 + 30/Q (Q - ilość sztuk produkcji), zaś funkcja utargu R = 4Q, wyznacz próg rentowności firmy. Czy próg rentowności zmieni się, gdy funkcja utargu przyjmie postać R = 3Q?

5. Koszty produkcji

1. Pani Zosia prowadzi samodzielnie zakład krawiecki. W ubiegłym roku jej utarg wyniósł 55.000 £, a koszty bezpośrednie 27.000 £. Kapitał finansowy włożony w działalność zakładu wynosił przez cały rok 25.000 £. Stopa procentowa wynosiła 10%. Gdyby Pani Zosia zdecydowała się podjąć pracę zarobkową w dużej firmie, mieszczącej się nieopodal, mogłaby tam zarobić 21.000 £. Oblicz:

1. koszt księgowy,

2. zysk księgowy,

3. koszt alternatywny pracy własnej,

4. koszt alternatywny wyłożonego kapitału,

5. łączny koszt ekonomiczny,

6. zysk ekonomiczny (nadzwyczajny).

2. Z Warszawy do Gdańska można polecieć samolotem lub pojechać pociągiem. Bilet lotniczy kosztuje 190 zł, lot trwa 1 godz. Bilet na pociąg kosztuje 60 zł, jazda trwa 4 godziny. Wyjaśnij, jaki będzie najbardziej ekonomiczny sposób podróży z punktu widzenia przedsiębiorcy, którego czas kosztuje 80 zł za godzinę i studenta, którego godzina jest warta 10 zł.

3. Właśnie dostałaś/eś nową pracę. Zarabiasz 50 zł za godzinę. Już w drugim tygodniu pracy masz towarzyszyć swojemu szefowi w podróży służbowej. Do wyboru masz pociąg i samolot. Twój szef na pewno pojedzie pociągiem, ponieważ nie znosi latania. Czy będziesz mu towarzyszyć, czy raczej wybierzesz samolot, biorąc pod uwagę, że bilet na pociąg kosztuje 80 zł i podróż trwa 6 godzin, zaś bilet na samolot jest droższy o 350%, podróż samolotem trwa godzinę. Przy jakiej stawce godzinowej zmienił(a)byś zdanie?

4. Pani Nowak i pan Kowalski założyli do spółki sklep. Przed założeniem sklepu pani Nowak pracowała w Żuczku i zarabiała 600 zł miesięcznie. Pan Kowalski był tramwajarzem i zarabiał 1000 zł miesięcznie. Oboje są właścicielami pomieszczenia, w którym urządzili sklep. W przeszłości wynajmowali je osobom trzecim za 1500 zł miesięcznie. Jakie są koszty alternatywne prowadzenia sklepu przez panią Kowalską i pana Nowaka? Wiedząc, że koszt księgowy prowadzenia własnego biznesu wynosi 6000 zł, a miesięczne utargi 9000 zł oblicz zyski księgowe oraz zyski ekonomiczne z prowadzenia sklepu. Co bardziej się opłaca prowadzenie sklepu czy praca w poprzednich miejscach zatrudnienia.

5. Joanna jest świeżo upieczoną panią doktor i stoi na progu życiowej decyzji dotyczącej kupna samochodu jako własnego narzędzia pracy aby móc jeździć do chorych. Za używany samochód musi zapłacić 8.000 zł. Przychody Joanny z prywatnej praktyki wynoszą 1500 zł miesięcznie. Koszty benzyny wynoszą 200 zł miesięcznie. Joanna mogłaby zatrudnić się w przychodni po sąsiedzku za 750 zł miesięcznie. Nie musiałaby wówczas kupować samochodu, a pieniądze mogłaby trzymać na lokacie oprocentowanej 5% w skali roku. Oblicz koszt księgowy, koszt ekonomiczny, zysk księgowy i zysk ekonomiczny z działalności Joanny.

6. Pan Zbyszek jest właścicielem magla. Miesięczne przychody z magla wynoszą 1500 zł. Koszty związane z opłatami za prąd wynoszą 800 zł. Gdyby Pan Zbyszek zamknął swój zakład mógłby starać się o wcześniejszą emeryturę, która wynosi 700 zł, ponadto mógłby wynająć pomieszczenie po maglu na skład cebulek tulipanów co przyniosłoby mu dochód w wysokości 250 zł miesięcznie. Oblicz koszt księgowy prowadzenia magla, zysk księgowy z tej działalności, koszt alternatywny pracy Pana Zbyszka, koszt alternatywny kapitału pana Zbyszka, łączny koszt ekonomiczny, oraz zysk ekonomiczny z prowadzenia magla.

7. Firma „Kowalski Art. International” produkuje dwa typy landszaftów - „Jeleń na rykowisku” i „Zachód słońca nad jeziorem”. Oblicz koszty księgowe, zyski księgowe, koszt alternatywny pracy własnej Kowalskiego, koszt alternatywny kapitału, oraz zysk ekonomiczny firmy wiedząc że: Kowalski produkuje 8 „Jeleni na rykowisku” miesięcznie i sprzedaje je po 250 zł sztuka oraz 10 zachodów słońca, których cena rynkowa za sztukę wynosi 200 zł. Koszty miesięczne związane z produkcją obrazów kształtują się następująco: wynajem atelier 800 zł; farby, pędzle, płótna i ramy 500 zł, reklama 200zł, wynagrodzenie dla pomocnika 1000 zł. Kowalski gdyby zrezygnował z produkcji landszaftów mógłby się zatrudnić w szkole podstawowej jako nauczycie plastyki zarabiałby wówczas 800 zł, podobną pracę mógłby znaleźć jego pomocnik. Oblicz koszt księgowy oraz zysk księgowy z produkcji landszaftów, a także koszt ekonomiczny, oraz zysk ekonomiczny z prowadzenia tej działalności.

8. Jan Kowalski w celu podniesienia swoich kwalifikacji zawodowych zapisuje się na trzymiesięczny kurs rachunkowości, który kosztuje 1000 zł. Uczestnictwo w kursie wymaga jednak od pana Kowalskiego skorzystania z bezpłatnego urlopu, co oznacza utratę zarobku w wysokości 1800 zł. W celu opłacenia kursu Jan Kowalski musi wpłacić ze swojego rachunku bankowego 600 zł, a 400 zł musi pożyczyć z banku na pół roku. Utracone oprocentowanie z tytułu wycofania pieniędzy z banku wynosi 40 zł, zaś oprocentowanie zaciągniętego kredytu - 60 zł. Koszty związane z dojazdem na kurs wynoszą 100 zł. Oblicz wartość utraconych alternatywnych możliwości rozdysponowania posiadanych przez Jana Kowalskiego zasobów pieniężnych i czasu.

Źródło: Zalega…

9. Stanisław Nowak posiadane przez siebie pieniądze w kwocie 300 tys. zł może zainwestować w piekarnię, albo może ulokować je na koncie terminowym w banku (stopa procentowa 10%) zatrudniając się jednocześnie w firmie, w której otrzymuje miesięczne wynagrodzenie w wysokości 2500 zł. Prowadząc piekarnię pan Nowak jest w stanie osiągnąć w ciągu roku dochód w wysokości 200 tys. zł. Koszty prowadzenia piekarni w ciągu roku przedstawiają się następująco (w zł):

- wynagrodzenie pracowników - 60 000,

- czynsz - 15 000,

- energia - 10 000,

- reklama - 40 000,

- inne wydatki - 5 000.

Jaką decyzję powinien podjąć pan Nowak: uruchomić piekarnię, czy wpłacić pieniądze do banku?

Źródło: Zalega…

10. Poniższe dane zawarte w poniższej tabeli charakteryzują sytuację firmy Jasia Kwiatkowskiego oraz warunki jej działania.

Wyszczególnienie	Wartość
Wielkość sprzedaży wyrobu A	10.000
Wielkość sprzedaży wyrobu B	5.000
Wielkość sprzedaży wyrobu C	3.000
Cena dobra A	2
Cena dobra B	4
Cena dobra C	7
Amortyzacja	3.000
Wynagrodzenie zatrudnionych pracowników (do produkcji, przyp. Autora)	15.000
Składka ZUS	40%
Odsetki od zaciągniętych kredytów	4.000
Surowce do produkcji	5.000
Koszt czasu pracy Jasia Kwiatkowskiego	6.000
Rynkowa wartość majątku firmy	100.000
Stopa procentowa	20%
Podatek od zysku	40%

1. koszty stałe,

2. koszty zmienne,

3. koszty całkowite,

4. koszty alternatywne,

5. przychód całkowity,

6. zysk księgowy brutto,

7. zysk księgowy netto,

8. zysk ekonomiczny.

Firma Jasia Kwiatkowskiego funkcjonuje w krótkim czy długim okresie? Uzasadnij odpowiedź.

(Źródło: 4.3/68, Zalega)

11. Poniższe dane zawarte w tabeli charakteryzują pewną firmę produkującą szlafroki damskie i męskie oraz warunki jej działania.

Wyszczególnienie	Wartość
Wielkość sprzedaży szlafroków damskich	20.000
Wielkość sprzedaży szlafroków męskich	12.000
Cena szlafroka damskiego	90
Cena szlafroku męskiego	80
Płace pracowników produkcyjnych	1.932.000
Koszt reklamy	138.000
Czynsz za wynajem lokalu	140.000
Płace pracowników biurowych	250.000
Inne wydatki biurowe	50.000
Podatek od zysku	30%

W oparciu o powyższe dane sporządź dla firmy rachunek wyników.

(Źródło: 4.7/69 Zalega…)

12. Na podstawie danych zawartych w tabeli oblicz koszt stały.

Wielkość produkcji (Q)	Koszt całkowity (TC)
0	100
1	105
2	135
3	168
4	190
5	210

13. Funkcja kosztów całkowitych pewnej firmy ma postać: TC = -60Q² + 6000Q + 1000, gdzie Q - wielkość produkcji.

1. Podaj analityczną postać funkcji: FC, VC, AFC, AVC, ATC, MC.

2. Oblicz koszty dla Q = 20.

3. Co stanie się z kosztami wyznaczonymi w punkcie b), jeśli przedsiębiorstwo zatrudni dodatkowych pracowników administracyjnych, których łączne wynagrodzenie wyniesie 80 jednostek?

14. Uzupełnij brakujące dane oraz przedstaw je graficznie.

Q	FC	VC	TC	AFC	AVC	ATC	MC
0			20
1			26
2			30
3			32
4			33
5			34
6			38
7			50

15. Uzupełnij brakujące dane oraz przedstaw je graficznie.

Q	FC	VC	TC	AFC	AVC	ATC	MC
0			20
1		6			6
2	20		30	10			4
3		15			5
4		18		5
5			40			8	2

(Źródło: 4.9/70 Zalega…)

16. Całkowity koszt produkcji 10 lizaków wynosi 20 zł, a 40 lizaków - 50 zł. Oblicz, ile będzie kosztowała produkcja 30 lizaków zakładając, że funkcja kosztów jest liniowa?

(Źródło: 4.10/70, Zalega…)

17. Jeżeli krzywa kosztów całkowitych beretów zapisana jest wzorem: TC = Q³ - 4Q² + 10Q, oblicz przy jakiej wielkości produkcji koszt przeciętny jest najmniejszy?

(Źródło: 4.11/70, Zalega…)

Źródło: Zalega…

18. Jakim rodzajom kosztów odpowiadają następujące miary: AC, BG, BD/OG, CF/OF, AF/OF?

19. Pan Ślimak jest właścicielem przedsiębiorstwa sprzedającego samochody. Ślimak kupuje samochody po C złotych każdy, nie mając przy tym żadnych innych kosztów.

1. Napisz równanie na koszt całkowity (TC) przedsiębiorstwa Ślimaka przy założeniu, że sprzedaje on y samochodów. TC(y) = ______________________

1. Jaki jest koszt przeciętny ATC(y) =______________________

2. Napisz funkcję kosztu krańcowego: MC(y) =______________________

3. Załóżmy, że Ślimak musi zapłacić każdego roku b złotych jako opłatę za reklamy telewizyjne. Krzywa kosztów całkowitych wygląda teraz następująco: TC(y) = _____________, kosztów przeciętnych ATC(y) = _____________ , kosztów krańcowych zaś MC(y) = _____________

20. Mając daną funkcję kosztu całkowitego przedsiębiorstwa (wariant nieproporcjonalnie zmieniających się kosztów) wyznacz graficznie funkcje kosztów: MC, AVC, ATC (konieczne jest uzasadnienie przebiegu poszczególnych funkcji i ich punktów charakterystycznych).

21. W okresie krótkim, gdy rośnie produkcja, to:

1. koszty krańcowe najpierw rosną a później maleją,

2. koszty całkowite początkowo rosną a później maleją,

3. gdy koszty krańcowe maleją, koszty przeciętne rosną,

4. koszty krańcowe najpierw maleją a później rosną.

6. Wolna konkurencja

Pytania ogólne

1. Co wynika z założenia dotyczącego modelu konkurencji doskonałej mówiącego o tym, iż konsument dysponuje pełną wiedzą dotyczącą rynku?

2. Dlaczego przedsiębiorstwa doskonale konkurencyjne charakteryzują się brakiem wysokich kosztów stałych.

3. Wyjaśnij dlaczego przedsiębiorstwo doskonale konkurencyjne nie określa ceny swoich produktów. Co by się stało gdyby chciało ustalić cenę poniżej ceny rynkowej? Co by się stało gdyby ustaliłoby cenę swoich produktów powyżej ceny rynkowej?

4. Co stało by się w gałęzi doskonale konkurencyjnej w krótkim i długim okresie jeśli jedno z przedsiębiorstw wprowadziło nową technologię pozwalającą obniżyć koszty produkcji?

5. Narysuj krzywą popytu dla przedsiębiorstwa doskonale konkurencyjnego i dla gałęzi doskonale konkurencyjnej.

6. Dlaczego w warunkach równowagi przedsiębiorstwa doskonale konkurencyjne produkują w optimum technicznym?

7. Dlaczego w przypadku przedsiębiorstw doskonale konkurencyjnych utarg krańcowy jest równy cenie?

8. Wyjaśnij czy możliwe jest istnienie zysków księgowych przy ujemnych zyskach ekonomicznych, dlaczego?

9. Dlaczego spadek ceny produktu przedsiębiorstwa doskonale konkurencyjnego poniżej przeciętnych kosztów całkowitych może nie spowodować w krótkim okresie zaprzestania produkcji?

10. Załóżmy, że pewna gałąź doskonale konkurencyjna produkuje „polski kawior”. Wyjaśnij jak w krótkim i długim okresie na sytuację firm i całej gałęzi wpłynie pojawienie się informacji w poczytnej prasie o cudownych właściwościach zdrowotnych „polskiego kawioru”.

Zadania

1. Wyjaśnij treść ekonomiczną równania:

AR = MR = ATC = MC.

Przedstaw powyższe równanie na wykresie.

2. Uzupełnij brakujące dane i skomentuj sytuację ekonomiczną przedsiębiorstwa. Czy przedsiębiorstwo powinno zmienić poziom wytwarzanej produkcji?

p	Q	TR	TC	FC	VC	ATC	AVC	MC
		36000	36000		30000	min.	10	12

3. Przedsiębiorstwo ponosi koszty stałe 2000 zł miesięcznie oraz koszt przeciętny zmienny 1,60 zł na jednostkę produktu. Jeśli w ciągu miesiąca może ono sprzedać 5000 sztuk swego wyrobu po cenie 1,8 zł za sztukę, to na krótką metę powinno:

1. wstrzymać produkcję, gdyż nie uzyskuje zwrotu kosztów stałych,

2. kontynuować produkcję, ponieważ uzyskuje zwrot kosztów stałych,

3. wstrzymać produkcję, ponieważ nie uzyskuje zwrotu kosztów zmiennych,

4. kontynuować produkcję, ponieważ uzyskuje zwrot kosztów zmiennych.

4. Mając do dyspozycji następujące dane:

• AFC = 48,

• AVC = 78,

• ATC = 126,

Zaznacz właściwe decyzje przedsiębiorcy przy danym poziomie ceny.

p	Produkować z zyskiem	Produkować mimo straty	Wstrzymać produkcję
136
54
84
80
48

5. Firma funkcjonująca w warunkach konkurencji doskonałej produkuje słoiki. Funkcja kosztu stałego ma postać FC = 100 a kosztu zmiennego VC = 2Q²-10Q. Cena jednego słoika wynosi p = 2 zł za sztukę. Oblicz wielkość produkcji, przy której firma będzie maksymalizowała zysk.

6. Przedsiębiorstwo funkcjonujące w warunkach konkurencji doskonałej wytwarza parasolki. Koszty całkowite kształtują się zgodnie z funkcją: TC = 3Q³-6Q²+9Q. Odpowiedz na następujące pytania:

1. przy jakiej cenie przedsiębiorstwo osiągnie graniczny punkt opłacalności produkcji,

2. jakimi właściwościami charakteryzuje się ten punkt,

3. jaki zysk osiąga wtedy przedsiębiorstwo?

Źródło: T. Zalega, Mikroekonomia - ćwiczenia, WSPiZ, Warszawa 1999.

7. Funkcja kosztów całkowitych przedsiębiorstwa wolnokonkurencyjnego produkującego meble kuchenne dana jest jako: TC = Q²-4Q+36. Oblicz wielkość produkcji, przy której koszty przeciętne tego przedsiębiorstwa osiągną minimum. Przedstaw w postaci algebraicznej równanie krzywej podaży tego przedsiębiorstwa.

Źródło: T. Zalega, Mikroekonomia - ćwiczenia, WSPiZ, Warszawa 1999.

8. Funkcja kosztów całkowitych przedsiębiorstwa działającego w warunkach konkurencji doskonałej dana jest jako: TC = 10Q²+200. Przedsiębiorstwo to wytwarza żyrandole, których cena rynkowa wynosi 100 zł za sztukę. Oblicz ilość równowagi w sytuacji, gdy przedsiębiorstwo znajduje się w optimum ekonomicznym.

Źródło: T. Zalega, Mikroekonomia - ćwiczenia, WSPiZ, Warszawa 1999.

9. Sytuację przedsiębiorstwa działającego na rynku konkurencji doskonałej opisują następujące dane:

TR = 17280

TC = 19200

ATC = 10

AVC = 8,98

MC = 9

Oblicz wielkość produkcji tego przedsiębiorstwa, cenę po której sprzedawany jest produkt, zysk przedsiębiorstwa. Ustal czy przedsiębiorstwo powinno kontynuować swoją produkcję.

10. Uzupełnij poniższą tabelkę. Przedstaw sytuację każdej firmy graficznie.

Firma	p	Q	TR	MR	TC	FC	VC	ATC min.	AVC	MC	Zysk ekon.	Zysk jedn.	Koszt księg.	Zysk norm.
I		4000	100000			20000			20				90000
II			75000		96000		75000		5					16000
III	4	2000			7000		6000							1260

Źródło: M. Nasiłowski, System rynkowy. Podstawy mikro- i makroekonomii, Wydawnictwo Key Text, Warszawa 2000.

11. Poniższa tabela ilustruje sytuację przedsiębiorstw w warunkach doskonałej konkurencji przy danym poziomie produkcji Q^*. Scharakteryzuj długookresową i krótkookresową ekonomiczną sytuację każdego z przedsiębiorstw (należy uzupełnić brakujące liczby i sporządzić rysunek). (Q^* - poziom produkcji w optimum ekonomicznym)

Firma	p	Q^*	TR	TC	FC	VC	ATC	AVC	MC	Koszt księg.	Zysk norm.	Zysk nadzwycz.
A	5		8000		2000		min.		5		1000
B		4000	24000	23000	7000					19000
C	8		160				12	9			50

12. Przedstaw na wykresie model przedsiębiorstwa doskonale konkurencyjnego, a następnie zaznacz odpowiednie odcinki, pola lub fragmenty krzywych:

• poziom ceny, dla którego przedsiębiorstwo osiąga tylko zysk normalny,

• poziom ceny zamknięcia przedsiębiorstwa,

• obszar odpowiadający kosztom stałym przy zysku normalnym,

• przedział cen w jakim przedsiębiorstwo zdecydowałoby się działać w krótkim okresie mimo ponoszenia strat,

• długookresową krzywą podaży przedsiębiorstwa,

• przedział cen, w którym przedsiębiorstwo może osiągnąć zyski nadzwyczajne.

13. Przedstaw na wykresie model przedsiębiorstwa doskonale konkurencyjnego w krótkim okresie, osiągającego zysk nadzwyczajny, a następnie zaznacz odpowiednie odcinki lub pola:

• jednostkowy zysk,

• koszt jednostkowy,

• wielkość utargu przeciętnego,

• obszar odpowiadający kosztom stałym.

Przy założeniu, że funkcja kosztów przedsiębiorstwa doskonale konkurencyjnego dana jest jako: TC = 4Q² - 20Q +64, zaś cena wynosi 60 jednostek, oblicz wielkość produkcji w optimum ekonomicznym i technicznym. Jaki wzór opisuje jej krótkookresową krzywą podaży?

14. Poniższy wykres przedstawia model przedsiębiorstwa w doskonałej konkurencji. Opisz osie i krzywe. Wyjaśnij, co wyrażają następujące pola i odcinki: BPGD, ABDE, OAEQ, OPGQ, OBDQ, EQ, DE, DG, GQ.

15. Tabela przedstawia sytuację trzech przedsiębiorstw doskonale konkurencyjnych działających w niezależnych od siebie gałęziach. Wiedząc, że wszystkie te firmy optymalizują produkcję uzupełnij tabelę, wykonaj wykresy ilustrujące sytuacje firm A, B i C. Skomentuj po kolei sytuację tych przedsiębiorstw, co może być przyczyną sytuacji w jakich się znalazły.

Firma	Q	P	AR	MR	TR	FC	AFC	VC	AVC	TC	ATC	MC	П
A		5			20000	2000							0
B	150		10				2			1200
C				15		500	5		12

16. Oto dane dotyczące utargów i kosztów przedsiębiorstwa doskonale konkurencyjnego „Brzydkie kaczątko” produkującego tusz do rzęs. AR=5, AFC = 4, ATC = 7, MC = 8 Narysuj wykres ilustrujący sytuację przedsiębiorstwa. Co byś doradził właścicielowi „Brzydkiego kaczątka”.

17. Poniższe dane dotyczą utargów i kosztów przedsiębiorstwa produkującego nawóz do kwiatów doniczkowych. MR=9, ATC=7, MC=6. Przedstaw graficznie sytuację firmy. Jaką decyzję powinien podjąć producent nawozu do kwiatów doniczkowych aby zmaksymalizować zysk. Co stanie się w tej gałęzi w długim okresie.

18. Poniższy wykres przedstawia sytuację firmy „Alte Hexe” produkującej krem na zmarszczki.

1. Na jakim rynku działa „Alte Hexe”?

2. Zaznacz pole kosztów stałych w sytuacji gdy przedsiębiorca dąży do maksymalizacji zysku.

3. Zaznacz krótkookresową funkcję podaży producenta kremu.

4. Co się stanie z sytuacją firmy w długim okresie?

5. Jaki wpływ na sytuację firmy miałoby ujawnienie badań wskazujących na niekorzystne skutki uboczne kremu na zmarszczki, gdyby firma znajdowała się w długookresowej równowadze?

19. Z wyliczeń producenta zegarów szafowych działającego na rynku doskonale konkurencyjnym wynika, że produkując 20 zegarów miesięcznie koszty stałe na jednostkę produkcji wynoszą AFC = 20 zł, a przeciętne koszty zmienne AVC = 45zł i są równe kosztom krańcowym. Co powinien zrobić producent zegarów przy danych poziomach cen za zegar:

1. 19zł

2. 35zł

3. 55zł

4. 75zł

20. Pewne przedsiębiorstwo doskonale konkurencyjne produkuje skarpetki. Funkcja przeciętnych kosztów stałych tego przedsiębiorstwa ma postać AFC=600/Q, natomiast funkcja przeciętnych kosztów zmiennych jest dana wzorem AVC=2. Rynkowa cena pary skarpetek wynosi P=5zł. Oblicz próg rentowności tego przedsiębiorstwa.

21. Firma „Narcyz” funkcjonująca na rynku doskonale konkurencyjnym produkuje kosmetyki dla mężczyzn. Funkcja kosztu zmiennego ma postać VC = Q²/50+10Q. Cena kremu dla mężczyzn wynosi P=30zł.

1. Oblicz wielkość produkcji, przy której firma będzie maksymalizowała zysk.

2. Wiedząc, że koszty stałe wynoszą FC = 5.000. Oblicz wielkość zysku tego przedsiębiorstwa.

3. Jakich zmian można się spodziewać w tej gałęzi w długim okresie.

22. Przeciętny koszt całkowity produkcji bukietów przez firmę „Nenufar” dany jest funkcją ATC=10+Q/2. Firma wyznacza wielkość produkcji na 90 bukietów miesięcznie, cena rynkowa bukietu wynosi 50 zł.

1. Ile wynoszą koszty stałe przy tej wielkości produkcji?

2. Oblicz koszty całkowite produkcji, oraz zysk.

3. Ile powinna produkować firma aby zmaksymalizować zysk?

23. Pewne przedsiębiorstwo produkujące lody grejpfrutowe działające na rynku doskonale konkurencyjnym, ponosi koszty stałe w wysokości 250, ponadto jego koszty zależne od wielkości produkcji kształtują się następująco VC = Q²/1000+Q.

1. Podaj postać analityczną funkcji kosztów całkowitych TC, przeciętnych kosztów zmiennych AVC, oraz kosztów krańcowych MC.

2. Wiedząc, że przedsiębiorstwo optymalizuje wielkość produkcji, a cena kulki lodów kosztuje 2 zł, oblicz ile wyniesie utarg przedsiębiorstwa?

3. Czy przedsiębiorstwo to generuje zysk księgowy?

24. Funkcja przeciętnych kosztów całkowitych firmy produkującej wykałaczki ma postać:

².

1. Przedstaw w postaci analitycznej funkcje kosztów FC i AVC.

2. Wiedząc, że producent wykałaczek działa na rynku doskonale konkurencyjnym, a cena jednego ogromnego opakowania wykałaczek wynosi 60zł oblicz ile ogromnych opakowań wykałaczek wyprodukuje firma maksymalizując zysk.

3. Czy firma ta może generować zysk normalny?

25. Pewne przedsiębiorstwo funkcjonujące w warunkach konkurencji doskonałej specjalizuje się w tworzeniu ogrodów zimowych. Funkcja kosztów całkowitych związanych z tworzeniem ogrodów zimowych ma postać: TC = 3Q³-120Q²+12000Q.

1. Wyznacz długookresową funkcję podaży tej firmy.

2. Po jakiej najniższej cenie zdecyduje się dostarczać ta firma ogrody zimowe w długim okresie, a po jakiej w krótkim okresie?

26. Funkcja kosztów całkowitych przedsiębiorstwa „Malinowska i córki” działającego w warunkach konkurencji doskonałej dana jest wzorem: TC=Q²+100Q+625. Przedsiębiorstwo to produkuje eleganckie stojaki na gazety. Cena rynkowa jednego stojaka na gazety wynosi 200 zł. Oblicz ilość równowagi oraz zyski całkowite firmy oraz na jednostkę produkcji w sytuacji, gdy przedsiębiorstwo znajduje się:

1. w optimum ekonomicznym

2. w optimum technicznym

3. scharakteryzuj te punkty.

27. Koszty całkowite pewnej firmy doskonale konkurencyjnej produkującej kredensy kształtują się następująco TC=4Q³-200Q²+3000Q.

1. Ile kredensów dostarczy firma produkując po najniższych kosztach?

2. Przy jakiej cenie firma wyprodukuje 50 kredensów?

3. Jeżeli cena rynkowa wynosi 3000zł ile kredensów wyprodukuje firma aby zmaksymalizować zysk.

28. Wyjaśnij znaczenie pojęcia „optimum techniczne”. Jaki jest warunek osiągnięcia optimum technicznego przez przedsiębiorstwo. Przedstaw na wykresie wielkość produkcji, przy której przedsiębiorstwo doskonale konkurencyjne osiągnie optimum techniczne (przedsiębiorstwo osiąga zysk normalny). Jak kształtuje się w tym przypadku stosunek optimum technicznego do ekonomicznego?

29. Wyjaśnij znaczenie pojęcia „optimum ekonomiczne”. Jaki jest warunek osiągnięcia optimum ekonomicznego przez przedsiębiorstwo. Przedstaw na wykresie wielkość produkcji, przy której przedsiębiorstwo doskonale konkurencyjne osiąga optimum ekonomiczne. Jak kształtuje się w tym przypadku stosunek optimum ekonomicznego do technicznego?

30. W poniższej tabeli przedstawione zostały dane opisujące sytuację trzech przedsiębiorstw w warunkach doskonałej konkurencji. Uzupełnij tabelę tak, aby przedsiębiorstwo maksymalizowało zyski lub (jeśli zysku osiągnąć się nie da) minimalizowało straty, a następnie scharakteryzuj sytuację każdego z nich i przedstaw ją na wykresie.

Przedsię-biorstwo	Cena p	Produkcja Q	Koszt całkowity TC	Koszt zmienny VC	Koszt stały FC	Koszt przeciętny całkowity ATC	Koszt przeciętny zmienny AVC	Koszt krańcowy MC	Koszt księgowy	Utarg całkowity TR	Utarg krańcowy MR	Zysk nor-malny	Zysk nadzwy-czajny
A	10					10	7,5			800		100
B		4000	14000		2000			3				1000
C				4000		6			5000	7000	7

31. Przedsiębiorstwo zabawek „Konik Garbusek” działa na rynku konkurencyjnym na którym cena zbytu wynosi 30 zł za sztukę. Wiemy, że koszty zmienne firmy są proporcjonalne do wielkości produkcji, jednostkowy koszt zmienny wynosi 6 zł, zaś całkowity koszt stały 120 zł.

• Zdefiniuj pojęcia kosztu zmiennego i stałego (przykłady).

• Przedstaw analitycznie funkcję kosztu całkowitego.

• Wylicz próg rentowności firmy.

• Ile wyniósłby próg rentowności gdyby całkowity koszt stały = 0?

7. Monopol

1. Dane: Q = 700-10P, FC = 1000, VC = 0,05Q² + 10Q. Wyznacz wielkość produkcji w optimum ekonomicznym oraz zysk całkowity monopolisty.

2. Przy założeniu, że koszt stały wynosi zero uzupełnij poniższą tabelę. Przy jakich rozmiarach produkcji monopolista wyznaczy cenę monopolową i jaki osiągnie maksymalny zysk. Przedstaw ten przykład na wykresie.

Q	p	MC	TR	TC	MR	AR
1	20	9
2	18	10
3	16	12
4	14	16
5	12	17
6	10	19

3. Przedstaw na wykresie model monopolu, a następnie zaznacz odpowiednie odcinki lub pola:

• wielkość produkcji maksymalizującej zysk,

• cenę monopolową,

• obszar zysku monopolowego,

• poziom produkcji pozwalający na osiągnięcie maksymalnego utargu całkowitego,

• całkowite koszty wytworzenia produkcji maksymalizującej zysk,

• poziom produkcji, przy której przeciętne koszty wytwarzania są najmniejsze.

4. Jedyny na rynku wytwórca szkieł powiększających wytwarza ich 1000 sztuk miesięcznie i sprzedaje je po 16 zł za sztukę. Całkowite koszty wytwarzania wynoszą 6000 zł. Prosta elastyczność cenowa popytu na szkła powiększające wynosi -1,6. Monopolista podniósł cenę o 4 zł, co spowodowało wzrost jednostkowych kosztów wytwarzania o 2 zł. Oblicz o ile zmienił się zysk monopolisty wskutek zmiany ceny. Czy decyzja o wzroście ceny była słuszna?

5. Przedstaw na wykresie model monopolu maksymalizującego zysk, a następnie zaznacz odpowiednie odcinki:

• jednostkowy zysk,

• koszt jednostkowy,

• wielkość utargu przeciętnego.

Przy założeniu, że funkcja kosztów przeciętnych całkowitych dana jest jako: ATC = Q + 2000/Q, zaś funkcja popytu na produkt monopolu ma postać: P = 600 - 3Q, oblicz wielkość produkcji, poziom ceny i zysk w optimum ekonomicznym.

6. Funkcja kosztów przedsiębiorstwa działającego w ramach konkurencji doskonałej jest następująca: TC=64-8X+X² (gdzie X - wielkość produkcji), zaś cena równa się 12.

1. Przy jakiej produkcji przedsiębiorstwo osiąga optimum techniczne? Jaki jest poziom produkcji i zysku w punkcie optimum ekonomicznego?

2. Przedsiębiorstwo jest teraz monopolistą o funkcji popytu P=80-10X. Jakie są: cena równowagi, produkcja i zysk? Ile musiałby produkować monopolista w optimum technicznym?

3. Porównaj i skomentuj wyniki uzyskane w podpunktach a i b.

7. Niech funkcja popytu na produkty monopolu (pełnego) ma początkowo postać: P(X) = 16 - 3X, a funkcja kosztu całkowitego C(X) = 6+X². Wskutek akcji reklamowej firmy funkcja popytu przesunęła się równolegle, co umożliwiło monopolowi powiększenie zysku o 9 jednostek. Podaj nową postać funkcji popytu.

8. Monopolista sprzedaje swój produkt według następującej funkcji popytu: P = 1800 - 20Q. Wyznacz cenę, która pozwoliłaby firmie maksymalizować zysk i cenę, która pozwoliłaby maksymalizować utarg całkowity, zakładając, że funkcja kosztów opisana jest równaniem TC(Q) = 10Q² + 1000.

9. Wyjaśnij znaczenie pojęcia „optimum ekonomiczne”. Jaki jest warunek osiągnięcia optimum ekonomicznego przez przedsiębiorstwo. Przedstaw na wykresie wielkość produkcji, przy której monopolista zysk osiąga optimum ekonomiczne. Jak kształtuje się w tym przypadku stosunek optimum ekonomicznego do technicznego?

10. Narysuj wykres utargu całkowitego, przeciętnego i krańcowego oraz krzywej popytu w modelu monopolu. Co możesz powiedzieć o elastyczności cenowej popytu na produkcję przedsiębiorstwa monopolistycznego i jakie ma to znaczenie dla producenta.

11. Popyt na produkt monopolisty opisuje równanie: Q = -0,5P + 100, zaś funkcja przeciętnych kosztów zmiennych tego przedsiębiorstwa ma postać: AVC = 0,5Q + 10.

1. Oblicz wielkość produkcji maksymalizującej zysk.

2. Wiedząc, że koszty stałe przedsiębiorstwa wynoszą 800 oblicz wielkość zysku.

12. Poniższy wykres przedstawia sytuację pewnej firmy produkującej maszyny samoczynnie prasujące koszule.

1. Zaznacz pole całkowitych kosztów zmiennych w sytuacji gdy przedsiębiorca dąży do maksymalizacji zysku.

2. Jaką decyzję powinien podjąć producent w długim okresie?

3. Zaznacz poziom produkcji, przy którym firma maksymalizuje utarg całkowity.

4. Jaki wpływ na sytuację tej firmy może mieć pojawienie się mody na maszyny samoczynnie prasujące koszule?

13. Przedstaw na wykresie model monopolu zaznaczając wielkość produkcji maksymalizującej zysk i cenę monopolową, a następnie pokaż jak zmieni się optimum ekonomiczne tego przedsiębiorstwa w przypadku spadku popytu na jego produkty (przy nie zmienionych kosztach wytwarzania).

14. Przedstaw na wykresie model monopolu zaznaczając wielkość produkcji maksymalizującej zysk i cenę monopolową, a następnie pokaż jak zmieni się optimum ekonomiczne tego przedsiębiorstwa na skutek wzrostu kosztów wytwarzania (przy założeniu, że krzywa popytu i utargu krańcowego nie zmieni swojego położenia).

15. Porównaj efektywność monopolu i przedsiębiorstwa doskonale konkurencyjnego?

16. Monopol ma funkcję popytu o postaci:

X = 144/P² gdzie X wielkość popytu, a P- cena.

Jego koszt zmienny jednostkowy jest AVC = X^1/2, zaś koszt stały FC = 5.

1. Przy jakiej cenie firma maksymalizuje zysk i dla jakiej wielkości produkcji?

2. Jaki jest zysk maksymalny?

c) Przypuśćmy, że rząd wprowadza maksymalną cenę. Nie może ona przekroczyć 4 zł. Ile będzie wówczas produkował monopol i jaki będzie jego zysk?

17. Jeżeli funkcja utargu całkowitego ma postać TR(q) = 100q - 5q², a funkcja kosztu całkowitego TC(q) = 150+50*q (gdzie: q - wielkość produkcji), oblicz zysk firmy oraz elastyczność cenową popytu w punkcie równowagi.

18. Funkcja popytu na wyroby firmy ma postać: Q = 30 - 0,25P. Jednostkowy koszt zmienny AVC = Q + 20, koszt stały FC = 400. Oblicz dla jakiej wielkości produkcji przedsiębiorstwo osiąga:

1. maksimum zysku,

2. maksimum utargu,

3. minimum całkowitego kosztu przeciętnego.

19. Wyjaśnij dlaczego monopol nie ma krzywej podaży.

20. W tabeli podano dane dotyczące pewnego przedsiębiorstwa monopolistycznego działającego w optimum ekonomicznym. Uzupełnij brakujące dane, narysuj wykres oraz skomentuj sytuację tego przedsiębiorstwa.

p	MR	TR	Q	ATC	MC	TC
	7	16.000		6		12.000

21. Przy założeniu, że funkcja kosztów dana jest jako: TC = 2Q² + 5.000, zaś funkcja popytu na produkt monopolu ma postać: P = 600 - 2Q_D, oblicz:

1. wielkość produkcji, poziom ceny i zysk w optimum ekonomicznym,

2. wielkość produkcji i cenę jeśli przedsiębiorstwo zdecyduje się produkować w optimum technicznym, ile wtedy wyniósłby jego zysk,

3. ile wyprodukowałoby przedsiębiorstwo, po jakiej cenie i z jakim zyskiem jeśli dążyłoby do maksymalizacji utargu całkowitego.

28

30

22,5

.B

.A

.C

30 35 43 75 90 120

wino

ostrygi

MC

ATC

AVC

P

P

AVC

ATC

MC

Q

MC

ATC

AVC

MR

P

P

MR

AVC

ATC

MC

Q

---