Fal Jacek 16.10.2007

Sprawozdanie z ćwiczenia nr 53

Pomiar względnego współczynnika załamania cieczy przy pomocy refraktometru Abbego.

1. Zagadnienia teoretyczne:

Odbicie całkowite wewnętrzne, odbicie światła zachodzące na granicy dwóch ośrodków przezroczystych charakteryzujących się współczynnikami załamania n1 i n2, n1>n2. Zjawisko obserwuje się w ośrodku o większym współczynniku załamania. Polega ono na odbiciu światła zachodzącym bez strat energii, nie towarzyszy mu załamanie światła. Obserwuje się go, gdy kąt padania (tj. kąt zawarty pomiędzy normalną do powierzchni a kierunkiem promienia światła) jest większy od tzw. kąta granicznego całkowitego odbicia wewnętrznego. Wartość tego kąta wyraża się wzorem:

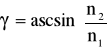
Pryzmat, element układu optycznego w postaci bryły o płaskich, na ogół nachylonych do siebie ścianach. Podstawowy typ pryzmatu to szklana bryła o prostokątnej podstawie i trójkątnym przekroju (pryzmat trójgraniasty). Promień światła wnikając do pryzmatu ulega załamaniu na obu skośnych powierzchniach pryzmatu.

Jeśli kąt pomiędzy płaszczyznami załamującymi pryzmatu oznaczyć γ (tzw. kąt łamiący pryzmatu), to sumaryczny kąt odchylenia promienia świetlnego δ związany jest z kątem łamiącym zależnością (w przybliżeniu, dla małych kątów padania):

δ = (n-1)γ,

gdzie: n - współczynnik załamania światła.

Zależność δ od n, przy jednoczesnej zależności n od długości fali światła (dyspersja), powoduje, że pryzmat rozszczepia światło białe, czyli pozwala uzyskać widmo światła. Stosowany do tego celu pryzmat nosi nazwę pryzmatu spektralnego. Pryzmaty takie stosuje się też do zmiany kierunku biegu promieni świetlnych (pryzmaty odbijające, odchylające lub odwracające).

Szczegółowe rozwiązania geometryczne takich pryzmatów to:

- pryzmat prostokątny (γ = 90°, światło pada i wydostaje się prostopadle do ścianek, wykorzystuje się tu odbicie całkowite wewnętrzne),

- pryzmat achromatyczny (sklejony z dwóch pryzmatów wykonanych z różnych gatunków szkła o tak dobranych n i γ, by kąty odchylenia dla światła czerwonego i niebieskiego były sobie równe),

- pryzmat rombowy (w przekroju romb, złożenie dwóch pryzmatów prostokątnych),

- pryzmat pentagonalny (o przekroju pięciokątnym, dwa całkowite wewnętrzne odbicia),

- pryzmat à vision directe (pryzmat o przekroju trapezowym, sklejony z 3 lub 5 pryzmatów trójgraniastych wykonanych z różnych gatunków szkła, dobranych tak, by promień o wybranej barwie przechodził bez odchylenia.

Modyfikacje: pryzmat Amiciego i pryzmat Dollonda), pryzmat Porro (dwa pryzmaty prostokątne, których krawędzie łamiące są wzajemnie prostopadłe, wykorzystywany jako układ odwracający.)

2. Wykonanie ćwiczenia:

1. Odsłonić okienko oświetlające pryzmat 1 P i odchylić oprawę z pryzmatem nakrywkowym w górę do oporu. Sprawdzić czy powierzchnia pryzmatów jest sucha i czysta.

2. Za pomocą bagietki szklanej przenieść na powierzchnię pomiarową pryzmatu refraktometrycznego kilka kropel przeznaczonej do badania cieczy tak, aby po zamknięciu pryzmatów cała powierzchnia pomiarowa była pokryta cieczą. Nie dotykać palcami powierzchni pryzmatów!

3. Opuścić pryzmat nakrywkowy i docisnąć do płaszczyzny pomiarowej. Odczekać chwilę, aby zrównały się temperatury cieczy i pryzmatów. Oświetlić okienko pryzmatu P₁ używając w tym celu lampki lub ustawić refraktometr w ten sposób, aby na okienko oświetlające padało światło rozproszone. Zwierciadło znajdujące się w dolnej ściance pryzmatu P₂ powinno zasłaniać otwór.

4. Regulując pokrętłami znajdującymi się na refraktometrze uzyskać ostre, wyraźne, barwne rozgraniczenie jasnego i ciemnego tła w polu widzenia. Obrotem pokrętła drugiego naprowadzić linię graniczną dokładnie na środek krzyża w górnym okienku okularu. Pionowa linia w dolnym okienku okularu wskaże wówczas na podziałce wynik pomiaru współczynnika załamania (górna podziałka). Odczytać wartość współczynnika załamania badanej cieczy, pomiary powtórzyć kilkakrotnie.

5. Wyznaczyć współczynnik załamania n dla roztworów o różnym stężeniu p .

6. Sporządzić wykres zależności współczynnika załamania n od stężenia roztworu p.

3. Tabela pomiarowa:

Tabela nr 1.

pi%	ni	ni ni
[%]	[---]	[---]
10	1,371 1,374 1,372	1,372 0,001
20	1,393 1,394 1,395	1,394 0,001
30	1,403 1,404 1,401	1,403 0,001
40	1,418 1,419 1,417	1,418 0,001
50	1,447 1,446 1,447	1,44 0,001
60	1,449 1,448 1,450	1,449 0,001
70	1,464 1,463 1,465	1,464 0,001
80	1,475 1,474 1,473	1,474 0,001
90	1,479 1,480 1,479	1,479 0,001

Tabela nr 2.

p% [%]	ni
90	1,479	1,478	1,476	1,478	1,484
		1,48	1,477	1,482	1,481	1,479
		1,479	1,478	1,481	1,479	1,48
		1,481	1,48	1,477	1,483	1,482

4. Obliczenia:

Współczynniki załamania cieczy obliczono uśredniając uzyskane wyniki.

Wartości obliczone zawarte są w tabeli.

Przebieg zmienności współczynnika załamania cieczy wraz ze wzrostem stężenia procentowego ilustruje wykres n_i=f(p%).

W celu obliczenia błędu pomiaru współczynnika załamania cieczy, dla wybranego stężenia (90%) przeprowadzono 20 pomiarów. Przedstawione są one w tabeli nr 2.

Na podstawie tych pomiarów liczymy błąd współczynnika załamania cieczy jako odchylenie standardowe średniej arytmetycznej.

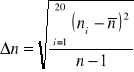
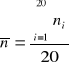
Tabela pomocnicza do wykresu funkcji Gaussa:

Alfa=

Prawdopodobieństwo = liczność/ilość pomiarów(20)

alfa	liczność	prawdopodobieństwo
-0,004 -0,003 -0,002 -0,001 0 0,001 0,002 0,003 0,004	1 2 3 3 4 3 2 1 1	0,05 0,1 0,15 0,15 0,2 0,15 0,1 0,05 0,05

Na podstawie tej tabeli wykonano wykres funkcji Gaussa rozkładu prawdopodobieństwa wystąpienia danego pomiaru.

5. Wykresy:

6. Wnioski:

Celem ćwiczenia było wyznaczenie względnego współczynnika załamania cieczy za pomocą refraktometru Abbego. Uważam, że doświadczenie zostało wykonane prawidłowo o czym świadczyć może niewielki błąd. Odstępstwa od wykładniczej formy wykresu dla stężeń 30-50% mogą świadczyć o błędach popełnionych podczas wykonywania ćwiczenia.

---