Wstęp teoretyczny.
1. Cel ćwiczenia.
Celem ćwiczenia jest wyznaczenie moduły sprężystości oraz modułu skręcenia pręta za pomocą wahadła torsyjnego.
W ćwiczeniu tym wykorzystywane są trzy dodatkowe obciążenia w postaci walców wykonanych z różnych materiałów. W przypadku, gdy na konstrukcję wahadła nałożone są symetrycznie dwa walce o jednakowej masie m to (przy założeniu, że ramie wahadła d jest znacznie większe niż wymiary walców, co w układzie laboratoryjnym jest spełnione) zmiana momentu bezwładności wyniesie:
2.Opis teoretyczny.
Jeśli jeden z końców długiego jednorodnego pręta sztywno zamocować, a do drugiego przyłożyć skręcający moment sił M, to koniec ten przekręci się o kąt φ, zgodnie z zależnością
Stała (dla danego pręta) wielkość D nosi nazwę modułu skręcenia (lub momentu kierującego). Liniowa zależność pomiędzy M i φ wyrażona wzorem zachodzi tylko dla niewielkich wartości M. W ogólnym przypadku zależność φ = φ(M) może być nieliniowa, lub nawet niejednoznaczna. Wielkość D nie charakteryzuje jednoznacznie właściwości materiału podczas skręcenia, dlatego wprowadza się wielkość nazwaną modułem sprężystości G.
Wprowadzony teraz zależnością wiążącą moduł sprężystości G oraz moduł skręcenia D. Po odchyleniu ciała o kąt α od położenia równowagi wytwarza się nowy stan równowagi, w którym reakcja pręta (moment M) równoważy moment siły zewnętrznej MZ. Po uwolnieniu ciała powstają drgania pod wpływem momentu siły
MZ = - D α
zwracającego ciało zawsze do położenia równowagi. Równanie ruchu ma więc postać analogiczną, jak dla wahadła grawitacyjnego
A zatem i okres drgań wyraża się tym samym wzorem
gdzie J jest momentem bezwładności drgającej bryły względem zadanej osi obrotu.
Wielkość modułu skręcenia D musimy określić w zależności od warunków fizycznych narzuconych w ćwiczeniu.
Rozważymy teraz przypadek, gdy siły działające na ciało powodują jego odkształcenie sprężyste (deformacja zanika po ustąpieniu siły odkształcającej F). W zależności od kąta utworzonego przez wektory siły działającej z powierzchnią ciała odkształconego rozróżniamy siły normalne tj. działające prostopadle do powierzchni, oznaczać je będziemy symbolem Fn, oraz siły styczne - działające stycznie do powierzchni - FS.
Naprężeniem normalnym σ nazywamy stosunek siły normalnej do pola powierzchni, na którą ta siła działa:
Miarą odkształcenia, jakiego ciało doznaje pod wpływem takiej siły, jest wielkość
W naszym ćwiczeniu wielkość G wyznaczamy wykorzystując drgania harmoniczne pręta metalowego, zachodzące pod wpływem sił sprężystości.
Każdy z elementów badanego drutu, skręconego przez siłę zewnętrzną, podlega deformacji ścinania prostego. Jako reakcja na tę siłę pojawia się w pręcie siła sprężystości powodująca powrót do położenia równowagi i w konsekwencji wywołująca zjawisko drgań. Wprowadzimy zależność między modułem sprężystości G, a momentem sił działającym na skręcony pręt. Rozważamy cylindryczny element pręta o promieniu wewnętrznym r*, grubości dr* i długości całego pręta l>> r* (Rys.1).
Dla pierścienia pokazanego na rysunku mamy:
gdzie s jest elementem łuku, ale
a więc
.
Rys. 1. Skręcenie pręta.
Mierząc okres T możemy wyznaczyć wartość modułu sprężystości:
Zależność między modułem skręcenia a modułem sprężystości wynika z zależności i jest następująca:
3. Opis układu pomiarowego.
Obiektem badań jest pręt o długości l i średnicy 2r, którego jeden koniec jest sztywno zamocowany w części górnej drugi zaś jest poddawany działaniu sił skręcających (Rys.2).
Rys.2. Wahadło torsyjne
W dalszej części pręta zamocowane jest ramie o długości 2d, na którego końcach znajdują się dwa stanowiska do zamocowania walców wykonanych z trzech różnych materiałów i posiadających różne masy (mosiądz, aluminium i plexiglas). Odchylony w płaszczyźnie poziomej układ wykonuje drgania torsyjne. Taki układ nosi nazwę wahadła torsyjnego. Jest to jeden z przykładów wahadła fizycznego. Jak w każdym wahadle fizycznym jego okres zależy od własnego momentu bezwładności.
4. Przebieg pomiaru.
1. Zapoznać się z budową wahadła torsyjnego.
2. Ustalić zakres amplitudy, w którym spełniony jest warunek .W tym celu należy umieścić wybraną parę walców na wahadle i wzbudzić przy pomocy pary sił drgania torsyjne zadając pewną początkową amplitudę. Mierząc czas 10 pełnych wahnięć, określić okres T1. Zmniejszyć amplitudę i tym samym sposobem wyznaczyć T2. Jeśli okaże się, że T1 T2 to należy zmniejszyć amplitudę do takiej wartości Φ, zaczynając od której dla wszystkich φ < Φ będzie wypełniona równość T1 = T2.
3. Zmierzyć liczbę pełnych drgań, po wykonaniu których amplituda zmniejszy się dwa razy (sprawdzenie słuszności nierówności ). 1〉〉n
4. Wprawić w drgania torsyjne (amplituda drgań nie większa od ustalonej na początku pomiarów) wahadło nie obciążone walcami i zmierzyć czas trwania 5 okresów T0 za pomocą stopera. Pomiar powtórzyć co najmniej 10 razy.
5. Powtórzyć pomiary wg punktu 4 dla wahadła obciążonego dwoma walcami: z mosiądzu umieszczonymi symetrycznie kolejno w odległościach d = 5, 7.5, 10, 12.5, 15 [cm],. (d = 0.05cm) Wyznaczone okresy oznaczyć odpowiednio: T1 , T2 , T3 , T4 , T5.
6. Wyniki wszystkich pomiarów przedstawić w formie tabeli.
Wyniki pomiarów:
Wymiary pręta: l=480![]()
1mm r=1,0![]()
0,1mm
Dane jednego ciężarka: m=65,53![]()
0,03g R=15,0![]()
0,1mm
Tabela 1.
Odległość |
||||||
Lp. |
5T0 [s] d=0 [cm] |
5T1 [s] d=5 [cm] |
5T2 [s] d=7,5 [cm] |
5T3 [s] d=10 [cm] |
5T4 [s] d=12,5 [cm] |
5T5 [s] d=15 [cm] |
1 |
3,4 |
4,1 |
4,9 |
5,6 |
6,3 |
7,1 |
2 |
3,6 |
3,9 |
4,8 |
5,7 |
6,5 |
7,1 |
3 |
3,4 |
4,0 |
4,7 |
5,3 |
5,9 |
7,3 |
4 |
3,2 |
3,9 |
4,6 |
5,2 |
6,1 |
6,9 |
5 |
3,2 |
3,8 |
4,5 |
5,4 |
6,3 |
6,8 |
6 |
3,4 |
4,0 |
4,8 |
5,3 |
6,0 |
7,1 |
7 |
3,4 |
3,7 |
4,6 |
5,4 |
6,1 |
7,0 |
8 |
3,2 |
4,3 |
4,7 |
5,5 |
5,9 |
6,9 |
9 |
3,4 |
3,9 |
4,5 |
5,3 |
6,0 |
7,0 |
10 |
3,5 |
3,9 |
4,8 |
5,2 |
6,2 |
7,4 |
![]()
=0,03g=0,03*10-3 kg ![]()
=0,05cm=0,5*10-3 m
Obliczenia:
1. Obliczamy momenty bezwładności I dla wszystkich 5 umieszczeń obciążników względem osi obrotu wahadła i błędy jakimi są one obarczone.
Korzystamy ze wzorów:
I=2md2 ![]()
=2*d2*![]()
![]()
Id=4*m*d*![]()
![]()
I=![]()
Tabela 2. Momenty bezwładności.
i |
di [m] |
Ii [kg*m2]* 10-3 |
|
|
|
1 |
0,050 |
0,328 |
0,150 |
6,553 |
6,551 |
2 |
0,075 |
0,737 |
0,338 |
6,928 |
9,835 |
3 |
0,100 |
1,311 |
0,600 |
13,106 |
13,120 |
4 |
0,125 |
2,048 |
0,928 |
16,383 |
16,409 |
5 |
0,150 |
2,949 |
0,135 |
19,659 |
19,705 |
2. Obliczamy średnie arytmetyczne pomierzonych okresów drgań, ponieważ mierzyliśmy czas 10 pełnych wahnięć otrzymane wyniki musimy podzielić przez 10.
10T=t => T=![]()
t- czas 10 pełnych wahnięć
Tśr i=![]()
Tabela 3. Czas jednego pełnego okresu.
n |
T0 |
T1 |
T2 |
T3 |
T4 |
T5 |
1 |
0,69 |
0,79 |
0,97 |
1,03 |
1,2 |
1,38 |
2 |
0,67 |
0,78 |
0, |
1,03 |
1,21 |
1,36 |
3 |
0,66 |
0,79 |
0,89 |
1,03 |
1,2 |
1,38 |
4 |
0,66 |
0,80 |
0,89 |
1,07 |
1,21 |
1,38 |
5 |
0,68 |
0,80 |
0,90 |
1,02 |
1,2 |
1,37 |
6 |
0,68 |
0,77 |
0,90 |
1,03 |
1,2 |
1,38 |
7 |
0,64 |
0,78 |
0,90 |
1,05 |
1,2 |
1,37 |
8 |
0,69 |
0,76 |
0,91 |
1,03 |
1,2 |
1,37 |
9 |
0,67 |
0,77 |
0,90 |
1,04 |
1,2 |
1,39 |
10 |
0,69 |
0,76 |
0,89 |
1,04 |
1,2 |
1,37 |
|
6,73 |
7,8 |
9,4 |
10,3 |
12,0 |
13,7 |
Tśr |
0,67 |
0,78 |
0,94 |
1,03 |
1,20 |
1,37 |
|
0,0046 |
0,0038 |
0,00 |
0,0043 |
0,0016 |
0,0021 |
3. Obliczamy D-moduł skręcenia i G- moduł sprężystości oraz średnie błędy kwadratowe tych wielkości.
Korzystamy ze wzorów:
D=4![]()
G=![]()
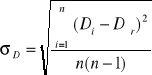
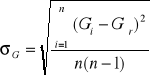
i |
Di [N*m]*10-4 |
Gi [ |
Dśr [N*m]*10-4 |
Gśr
[ |
[N*m]*10-3 |
[ |
1 |
8,17 |
2,497 |
|
22,272 |
1,645 |
0,503 |
2 |
|
|
|
|
|
|
3 |
8,329 |
2,445 |
|
|
|
|
4 |
8,175 |
2,498 |
|
|
|
|
5 |
8,125 |
2,483 |
|
|
|
|
Wnioski.
Celem ćwiczenia było wyznaczenie moduły sprężystości oraz modułu skręcenia pręta za pomocą wahadła torsyjnego. Ćwiczenie zakończyło się powodzeniem, bowiem moduł sprężystości oraz moduł skręcenia pręta oraz inne wartości zostały obliczone, a ich wartość zostały umieszczone w tabelach. Natomiast średnia wartość modułu skręcenia jest równa: Dśr =72,846x10-3[N*m] , a średnia wartość modułu sprężystości jest równa: : Gśr =22,272*1013[![]()
] . Natomiast średnie błędy kwadratowe tych wielkości są równe: ![]()
=1,645* 10-3 [N*m] oraz ![]()
=0,503*1013 [![]()
] . Według nas średnie błędy kwadratowe są dość duże, ale nie aż tak aby mogły dowieść o złym wyniku tego ćwiczenia laboratoryjnego. Warto też wspomnieć że wpływ na wyniki ma także klasa miernika(w tym przypadku stoper w telefonie komórkowym, ponieważ stoper laboratoryjny był zepsuty i uniemożliwiał dobry pomiar ) oraz to że wielkości pośrednie są obarczone własnymi błędami. Jest to rzecz warta ujęcia. Chcielibyśmy także zauważyć, że wszystkie obliczane wielkości, a także błędy, są ściśle związane z wartościami T0 i Ti (1<=i<=5) oraz z I0 i Ii (1<=i<=5).
Wyszukiwarka