TEORIA I TECHNIKA SYSTEMÓW

1. TWORZENIE MODELI I MODELOWANIE

2. IDENTYFIKACJA I ROZPOZNAWANIE

3. ANALIZA I PROJEKTOWANIE

4. STEROWANIE I KIEROWANIE

DR INŻ. ANDRZEJ ŻOŁNIEREK P.111, C-3

POJĘCIE SYSTEMU

IDEA WYODRĘBNIENIA SYSTEMU Z OTOCZENIA

IDEA BUDOWY SYSTEMU Z ELEMENTÓW ( PODSYSTEMÓW )

IDEA FUNKCJI SPEŁNIANEJ PRZEZ SYSTEM

IDEA OGRANICZONEJ ZMIENNOŚCI SYSTEMU W CZASIE

SYSTEM JEST PEWNĄ CAŁOŚCIĄ, W KTÓREJ WSPÓŁDZIAŁAJĄ WYODRĘBNIONE CZĘŚCI SKŁADOWE. FUNKCJONOWANIE SYSTEMU ZALEŻY OD FUNKCJI CZĘŚCI SKŁADOWYCH I ZWIĄZKÓW MIĘDZY NIMI. POWIĄZANIA CZĘŚCI SKŁADOWYCH

OKREŚLAJĄ STRUKTURĘ SYSTEMU.

CELE BUDOWY MODELU SYSTEMU

1. OPIS I WYJAŚNIENIE DZIAŁANIA MECHANIZMU SYSTEMU - MODEL FENOMENOLOGICZNY

2. PRZEWIDYWANIE ZACHOWANIA SIĘ SYSTEMU W PRZYSZŁOŚCI I PRZY RÓŻNYCH

WARUNKACH ODDZIAŁYWANIA NA SYSTEM - MODEL PROGNOSTYCZNY

3. WYBÓR WŁAŚCIWYCH ODDZIAŁYWAŃ WEJŚCIOWYCH SPEŁNIAJĄCYCH OKREŚLONE WARUNKI - MODEL DECYZYJNY ( W SZCZEGÓLNOŚCI WYBÓR OPTYMALNY)

4. WYBÓR STRUKTURY LUB PARAMETRÓW SYSTEMU , SPEŁNIAJĄCEGO OKREŚLONE ZADANIA - MODEL NORMATYWNY

ETAPY MODELOWANIA MATEMATYCZNEGO

1. SFORMUŁOWANIE CELÓW MODELOWANIA

2. WYBÓR KATEGORII MODELU I OKREŚLENIE JEGO STRUKTURY

3. IDENTYFIKACJA

4. ALGORYTMIZACJA OBLICZEŃ

5. WERYFIKACJA

MODELEM MATEMATYCZNYM SYSTEMU (OBIEKTU, PROCESU) JEST ZESTAW WZORÓW MATEMATYCZNYCH (OGÓLNIE ZESTAW RELACJI MATEMATYCZNO-LOGICZNYCH) OKREŚLAJĄCYCH ZALEŻNOŚCI POMIĘDZY WYRÓŻNIONYMI WIELKOŚCIAMI.

SĄ TO WIELKOŚCI WEJŚCIOWE I WYJŚCIOWE SYSTEMU, A SYSTEM TAKI NAZYWAMY

WZGLĘDNIE ODOSOBNIONYM.

W POJĘCIACH WEJŚCIE I WYJŚĆIE ZAWARTE JEST DOMNIEMANIE O ZWIĄZKU

PRZYCZYNOWO-SKUTKOWYM MIĘDZY TYMI WIELKOŚCIAMI, W TYM SENSIE , ŻE ZNAJĄC (OBSERWUJĄC) WEJŚCIE MOŻNA OKREŚLIĆ JAKIE BĘDZIE WYJŚCIE

WERYFIKACJA MODELU JEST TO PORÓWNANIE WYNIKÓW MODELOWANIA Z ZACHOWANIEM SIĘ SYSTEMU RZECZYWISTEGO Z PUNKTU WIDZENIA ZGODNOŚCI Z WIEDZĄ TEORETYCZNĄ ORAZ BADANIAMI EMPIRYCZNYMI

KRYTERIA WEWNĘTRZNE :

-ZGODNOŚĆ FORMALNA

-ZGODNOŚĆ ALGORYTMICZNA

KRYTERIA ZEWNĘTRZNE :

-ZGODNOŚĆ HEURYSTYCZNA

-ZGODNOŚĆ PRAGMATYCZNA

1.ZGODNŚĆ REPLIKATYWNA

2.ZGODNOŚĆ PREDYKATYWNA

3.ZGODNŚĆ STRUKTURALNA

DYNAMIKA SYSTEMÓW

SYSTEMY STATYCZNE

SYSTEMY DYNAMICZNE

WŁASNOŚCI DYNAMICZNE SYSTEMÓW WYNIKAJĄ Z DZIAŁANIA NASTĘPUJĄCYCH OGÓLNYCH ZASAD F I Z Y C Z N Y C H :

• PRZY OGRANICZONYCH WYDAJNOŚCIACH ŹRÓDEŁ , KAŻDA NIE NIESKOŃCZENIE MAŁA ZMIANA STANU ENERGETYCZNEGO LUB MATERIAŁOWEGO WYMAGA PEWNEGO CZASU (BEZWŁADNOŚĆ=INERCJA)

• KAŻDE SKOŃCZONE PRZEMIESZCZENIE SIĘ W PRZESTRZENI ZJAWISKA MATERIALNEGO WYMAGA PEWNEGO CZASU (OPÓŹNIENIE)

STAN SYSTEMU DYNAMICZNEGO

JEST TO NAJMNIEJSZA LICZBA DANYCH (WEKTOR STANU) , KTÓRYCH ZNAJOMOŚĆ W DANEJ CHWILI, PRZY ZNAJOMOŚCI WIELKOŚCI WEJŚCIOWYCH , POCZĄWSZY OD TEJ CHWILI - POZWALA JEDNOZNACZNIE OKREŚLIĆ STAN I WIELKOŚCI WYJŚCIOWE SYSTEMU W PRZYSZŁOŚCI.

WIELKOŚCI STANU SĄ WIĘC ZMIENNYMI WEWNĘTRZNYMI SYSTEMU, KTÓRE REASUMUJĄ W SOBIE CAŁĄ PRZESZŁOŚĆ I DETERMINUJĄ JEGO PRZYSZŁOŚĆ.

ZDETERMINOWANIE SYSTEMU WYNIKA Z POSTULATÓW :

• PRZYCZYNOWOŚĆ

• ZUPEŁNOŚĆ

UKŁADEM STEROWANIA NAZYWAMY ZESPÓŁ ZŁOŻONY Z OBIEKTU STEROWANIA I URZĄDZENIA STERUJĄCEGO - ODPOWIEDNIO POWIĄZANYCH FUKCJONALNIE ZE SOBĄ.

W OBIEKCIE STEROWANIA WYRÓŻNIAMY :

• SYGNAŁY WEJŚCIOWE (STERUJĄCE)

• SYGNAŁY ZAKŁÓCAJĄCE

• SYGNAŁY WYJŚCIOWE

SYGNAŁY, NAWET WTEDY, KIEDY SĄ WIELKOŚCIAMI FIZYKALNYMI LUB FIZYKALNIE WYOBRAŻALNYMI, NIE ZAWSZE MOŻNA W DANYM OBIEKCIE WYZNACZYĆ I NIE ZAWSZE MOŻNA ODDZIAŁYWAĆ NA NIE ZA POMOCĄ ROZPORZĄDZALNYCH SYGNAŁÓW STERUJĄCYCH.

SYGNAŁY MOGĄ BYĆ:

-MIERZALNE I STEROWALNE

-MIERZALNE I NIESTEROWALNE

-STEROWALNE I NIEMIERZALNE

-NIEMIERZALNE I NIESTEROWALNE.

MODEL MATEMATYCZNY TWORZYMY

1. NA PODSTAWIE PEŁNEJ ZNAJOMOŚCI ZJAWISK W POSZCZEGÓLNYCH OBIEKTACH ORAZ ICH POWIĄZAŃ MIĘDZY SOBĄ I Z URZĄDZENIAMI STERUJĄCYMI USTALA SIĘ ZALEŻNOŚCI MIĘDZY SYGNAŁAMI WYSTĘPUJĄCYMI W UKŁADZIE.

2. NA PODSTAWIE CZĘŚCIOWEJ ZNAJOMOŚCI ZJAWISK W SKŁADOWYCH OBIEKTACH I STRUKTURY UKŁADU FORMUŁUJE SIĘ WSTĘPNIE ZWIĄZKI MIĘDZY SYGNAŁAMI. NASTĘPNIE KORYGUJE SIĘ TE ZALEŻNOŚCI NA PODSTAWIE WYNIKÓW UZYSKANYCH EKSPERYMENTALNIE.

3. W PRZYPADKU NIEPEŁNEJ INFORMACJI A PRIORI O UKŁADZIE LUB BRAKU TEJ INFORMACJI OTRZYMUJE SIĘ DOŚWIADCZALNIE OKREŚLONE DANE I PO ODPOWIEDNIM ICH PRZETWORZENIU TWORZY MODEL MATEMATYCZNY

I D E N T Y F I K A C J A

OZNACZA WYZNACZENIE MODELU SYSTEMU NA PODSTAWIE BADAŃ EKSPERYMENTALNYCH. JEST TO OBSZERNY DZIAŁ TEORII I TECHNIKI SYSTEMÓW OBEJMUJĄCY RÓŻNE PROBLEMY, METODY I TECHNIKI DLA RÓŻNYCH PRZYPADKÓW SYSTEMÓW I ICH MODELI.

EFEKTEM KOŃCOWYM JEST A L G O R Y T M I D E N T Y F I K A C J I.

A NA L I Z A

1. ANALIZA ILOŚCIOWA

2. ANALIZA JAKOŚCIOWA

P R O J E K T O W A N I E (SYNTEZA) MOŻE TO BYĆ PODEJMOWANIE DECYZJI

PRZY ZMIENNYCH ZAKŁÓCENIACH MAMY DO CZYNIENIA ZE S T E R O W A N I E M.

BIEŻĄCE ZMIANY PROJEKTU SPOWODOWANE ZMIANAMI ZAKŁÓCEŃ I POLEGAJĄCE NA WYZNACZANIU ORAZ REALIZACJI UAKTUALNIANYCH DECYZJI NAZYWAMY STEROWANIEM.

W TEN SPOSÓB SYSTEM STERUJĄCY ODDZIAŁYWUJE NA OBIEKT STEROWANIA W OKREŚLONYM CELU, KTÓRYM JEST DOPROWADZENIE WYJŚCIA DO WARTOŚCI ZADANEJ LUB EKSTREMALNEJ ORAZ UTRZYMYWANIE OBIEKTU MOŻLIWIE BLISKO TYCH WARTOŚCI MIMO DZIAŁAJĄCYCH ZAKŁÓCEŃ.

PRZEPIS FORMALNY TO A L G O R Y T M S T E R O W A N I A.

KLASYFIKACJA UKŁADÓW STEROWANIA:

NA PODSTAWIE WŁASNOŚCI

• UKŁADY CIĄGŁE I DYSKRETNE

• UKŁADY LINIOWE I NIELINIOWE

• UKŁADY STACJONARNE I NIESTACJONARNE

• UKŁADY JEDNO I WIELOWYMIAROWE

• UKŁADY O STAŁYCH SKUPIONYCH I O PARAMETRACH ROZŁOŻONYCH

ZE WZGLĘDU NA ZADANIA

• UKŁADY AUTOMATYCZNEJ STABILIZAJI (REGULACJI STAŁOWARTOŚCIOWEJ)

• UKŁADY REGULACJI PROGRAMOWEJ

• UKŁADY NADĄŻNE (ŚLEDZĄCE)

ZE WZGLĘDU NA RODZAJ PROCESÓW PODLEGAJĄCYCH STEROWANIU

• UKŁADY STEROWANIA PROCESÓW JEDNOSTKOWYCH

• UKŁADY STEROWANIA KOMPLEKSOWEGO

ZE WZGLĘDU NA SPOSÓB REALIZACJI STEROWANIA I MOŻLIWOŚCI DOSTOSOWANIA SIĘ UKŁADÓW DO ZMIENIAJĄCYCH SIĘ WARUNKÓW PRACY

• UKŁADY ZWYKŁE (NIEADAPTACYJNE)

• UKŁADY ADAPTACYJNE

• UKŁADY OPTYMALNE

• UKŁADY NIEOPTYMALNE

METODY OPISU CIĄGŁYCH LINIOWYCH JEDNOWYMIAROWYCH OBIEKTÓW STEROWANIA

• RÓWNANIA RÓŻNICZKOWE OPISUJĄCE JEDNOWYMIAROWE OBIEKTY STEROWANIA ( W SZCZEGÓLNOŚCI RÓWNANIE WE-WY)

• ODPOWIEDŹ JEDNOSTKOWA (SKOKOWA)

• ODPOWIEDŹ IMPULSOWA

• TRANSMITANCJA OPERATOROWA

• TRANSMITANCJA WIDMOWA

• METODA PRZESTRZENI FAZOWEJ I PŁASZCZYZNY FAZOWEJ

• METODA ZMIENNYCH STANU

• CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE

• CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE:

1. CHARAKTERYSTYKA AMPLITUDOWO-FAZOWA

2. CHARAKTERYSTYKA AMPLITUDOWA

3. CHARAKTERYSTYKA FAZOWA

4. CHARAKTERYSTYKA SKŁADOWEJ RZECZYWISTEJ TRANSMITANCJI

5. CHARAKTERYSTYKA SKŁADOWEJ UROJONEJ TRANSMITANCJI

6. CHRAKTERYSTYKA LOGARYTMICZNA AMPLITUDOWA

7. CHARAKTERYSTYKA LOGARYTMICZNA FAZOWA

TYPOWE CZŁONY LINIOWE

• CZŁON PROPORCJONALNY

• CZŁON INERCYJNY PIERWSZEGO RZĘDU

• CZŁON CAŁKUJĄCY IDELNY

• CZŁON CAŁKUJĄCY Z INERCJĄ

• CZŁON RÓŻNICZKUJĄCY Z INERCJĄ

• CZŁON OSCYLACYJNY

• CZŁON INERCYJNY DRUGIEGO RZĘDU

• CZŁON OPÓŹNIAJĄCY

MODEL SYSTEMU PRODUKCYJNEGO (STATYCZNY)

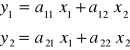
ilości surowców przerabianych w dwóch agregatach

ilość produktu i koszt produkcji

IDENTYFIKACJA

wyznaczenie
na podstawie układu czterech równań:

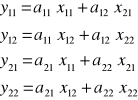
ANALIZA ILOŚCIOWA

jeżeli znamy wartości liczbowe parametrów
to

wstawiamy dane
do modelu i wyliczamy

PROJEKTOWANIE - PODEJMOWANIE DECYZJI

dla danych wartości a oraz zadanych wartości
,

można wyliczyć decyzje

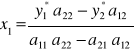
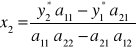
C h a r a k t e r y s t k ą ( o d p o w i e d z i ą ) s k o k o w ą

h(t) jednowymiarowego układu ( obiektu ) liniowego stacjonarnego nazywać będziemy odpowiedź tego układu na wymuszenie w postaci jednostkowej funkcji skokowej 1( t ) , przy zerowych warunkach początkowych.

C h a r a k t e r y s t k ą ( o d p o w i e d z i ą ) impulsową

g(t) jednowymiarowego układu ( obiektu ) liniowego stacjonarnego nazywać będziemy odpowiedź tego układu na wymuszenie w postaci funkcji Diraca ( t ) , przy zerowych warunkach początkowych.

T r a n s m i t a n c j ą o p e r a t o r o w ą

G( s ) jednowymiarowego układu ( obiektu ) liniowego stacjonarnego nazywać będziemy wielkość określoną jako stosunek transformaty odpowiedzi Y( s ) do transformaty wymuszenia U( s ) tego układu przy zerowych warunkach początkowych

G ( s ) = Y ( s ) / U ( s )

CZŁON INERCYJNY

Równanie różniczkowe wejście-wyjście:

k- współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym,

T- stała czasowa.

Charakterystyka skokowa:

Odpowiedź impulsowa:

Transmitancja:

CZŁON BEZINERCYJNY (proporcjonalny, wzmacniający)

Równanie różniczkowe wejście-wyjście:

k- współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym,

T- stała czasowa = 0.

Charakterystyka skokowa:

Odpowiedź impulsowa:

Transmitancja:

CZŁON CAŁKUJĄCY Z INERCJĄ

Równanie różniczkowe wejście-wyjście:

k- współczynnik wzmocnienia prędkościowego określony jako stosunek pochodnej odpowiedzi y do wymuszenia u w stanie ustalonym,

T- stała czasowa.

Charakterystyka skokowa:

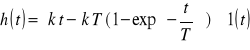
Odpowiedź impulsowa:

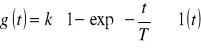
Transmitancja:

CZŁON CAŁKUJĄCY IDEALNY

Równanie różniczkowe wejście-wyjście:

k- współczynnik wzmocnienia prędkościowego określony jako stosunek pochodnej odpowiedzi y do wymuszenia u w stanie ustalonym,

T- stała czasowa = 0.

Charakterystyka skokowa:

Odpowiedź impulsowa:

Transmitancja:

CZŁON RÓŻNICZKUJĄCY Z INERCJĄ (rzeczywisty człon różniczkujący)

Równanie różniczkowe wejście-wyjście:

k- współczynnik wzmocnienia określony jako stosunek odpowiedzi y do pochodnej wymuszenia u w stanie ustalonym,

T- stała czasowa.

Charakterystyka skokowa:

Odpowiedź impulsowa:

Transmitancja:

CZŁON RÓŻNICZKUJĄCY

Równanie różniczkowe wejście-wyjście:

k- współczynnik wzmocnienia określony jako stosunek odpowiedzi y do pochodnej wymuszenia u w stanie ustalonym,

T- stała czasowa = 0.

Charakterystyka skokowa:

Odpowiedź impulsowa:

Transmitancja:

CZŁON OSCYLACYJNY

Równanie różniczkowe wejście-wyjście:

lub

k- współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym,

- okres drgań własnych nie tłumionych,

- pulsacja drgań własnych nie tłumionych,

- względny współczynnik tłumienia (
)

Charakterystyka skokowa:

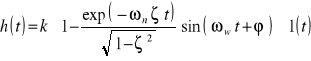
przy czym

- pulsacja drgań własnych tłumionych

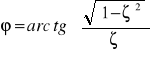
Odpowiedź impulsowa:

Transmitancja:

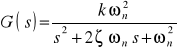
lub

CZŁON INERCYJNY DRUGIEGO RZĘDU

Równanie różniczkowe wejście-wyjście:

lub

k- współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym,

,
- stałe czasowe obiektu,

Transmitancja:

lub

,
,
,
,

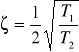
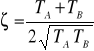
CZŁON OPÓŹNIAJĄCY

Równanie różniczkowe wejście-wyjście:

- współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u dla
,

- czas opóźnienia.

Charakterystyka skokowa:

Odpowiedź impulsowa:

Transmitancja:

---