1. ROZCIĄGANIE . PODSTAWOWE ZALEŻNOŚCI ( NAPRĘŻENIA, ODKSZTAŁCENIA, PRZEMIESZCZENIA)

Statyczna próba rozciągania- próba ta polega na powolnym rozciąganiu próbki aż do jej zerwania, wymuszając stałą prędkość przyrostu długości.

- równania równowagi

- warunki geometryczne

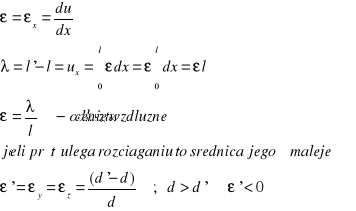
- związki fizyczne

2. ROZCIĄGANIE - OBLICZENIA WYTRZYMAŁOŚCIOWE

W obliczeniach wytrzymałościowych mamy trzy typy obliczen

- obliczenia sprawdzające Dane: N,A, σ_dop, σ_nieb; σ_nieb /σ = n

- wyznaczanie obiązenia dopuszczalnego Dane: A, σ_dop; N_dop = Aσ_dop

- wyznaczenie wymiarów ( dobór przekroju) Dane: N, σ_dop; A = N /σ_dop

3. WYKRES ROZCIĄGANIA STATYCZNA PRÓBA ROZCIAGANIA

F_H- wartość siły na granicy proporcjonalności R_H - granica proporcjonalności

F_spr- wartość siły na granicy spręzystosci R_spr - granica spręzystości

F_el - wartość siły dolnej granicy plastycznosci R_el - dolna granica plastycznosci

F_eh - wartość siły gornej granicy plastycznosci R_eh - gorna granica plastycznosci

F_m - największa siła rozciągająca dzialajaca na próbkę R_m - wytrzymałość na rozciaganie

Fu- sila wywołująca zerwanie Ru - naprężenia rozrywające

Próba polega na poddaniu odpowiednio ukształtowanej próbki działaniu siły rozciągającej w kierunku osiowym aż do jej zerwania. Przy próbie stat. Obciążenie wolno narasta z określoną prędkością. Próbę przeprowadza się na maszynach zwanych zrywarkami. Próbki posiadają część pomiarową o stałym przekroju i są zakończone główkami o zwiększonych wymiarach. Z pomiarów odkształceń na powierzchni ciała można wnioskować o odkształceniach wewnątrz ciała a z pomiarów całkowitej siły można wyliczyć naprężenia istniejące wewnątrz próbki. Próba rozciągania jest podstawową próbą wytrzymałościową

d_o - średnica początkowa próbki

d_u - średnica końcowa próbki

ΔL=L_u-L_o [mm] - bezwzględne wydłużenie próbki

A_p= ΔL/L_o 100% - względne wydłużenie próbki proporcjonalnej po zerwaniu

z=[d_o²-d_u²)/d_r²]100% - względne przewężenie próbki okrągłej

R_e=F_e/S_o [Mpa] - wyraźna granica sprężystości

Ru=Fu/S_u[MPa] -naprężenie rozrywające

Rm=F_m/S_o [MPa] - wytrzymałość na rozciąganie

4. CHARAKTERYSTYKI GEOMETRYCZNE FIGUR PŁASKICH

a) momenty statyczne [m³]

b) środek ciężkości [m]

c) momenty bezwładności [m⁴]

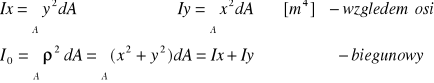
d)moment dewiacji (zboczenia)[m⁴]

e)promień bezwładności [m]

5. GŁÓWNE CENTRALNE MOMENTY BEZWLADNOSCI. TWIERDZENIE STEINERA.

Moment bezwładności I_o figury płaskiej względem ustalonego punktu 0, zwanego biegunem, definiuje się jako

gdzie ρ jest odległością elementu powierzchni o polu dA od punktu 0 (biegunowy mom. bezw.).

Centralne osie bezwładności - osie przechodzące przez srodek ciężkości przekroju.

Centralne momenty bezwładności - względem centralnych osi bezwładności.

Główne osie bezwładności - osie względem których moment dewiacji jest rowny 0.

Główne momenty bezwładności - względem głównych osi bezwładności

Główne centralne momenty bezwładności - względem głównych centralnych osi bezwładności

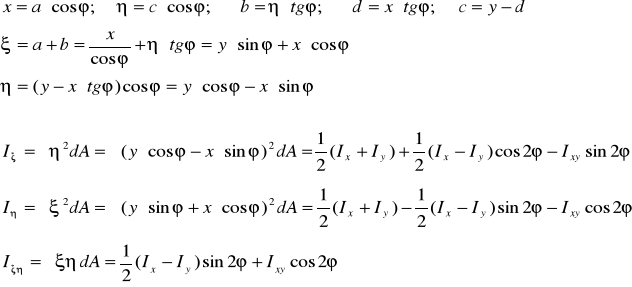
Główne osie bezwładności

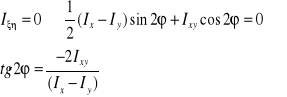
Główne momenty bezwładności

Twierdzenie Steinera.

Moment bezwładności figury płaskiej względem osi równoległej do centralnej osi (przechodzącej przez środek ciężkości ) równy jest sumie momentu bezwładności względem centralnej osi i iloczynowi pola powierzchni figury i kwadratu odległości pomiedzy osiami .

I_ξ = I_x + Ab², I_η = I_y + Aa² , I_ξη = I_xy + Aab

6. SKRĘCANIE. ZAŁOŻENIA. PODSTAWOWE ZALEŻNOŚCI ( naprężenia, odkształcenia, przemieszczenia)

Jeśli pręt obciążymy w płaszczyźnie prostopadlej do jego osi para sił o momencie K to sily wewnętrzne zredukuja się do momentu M_s którego kierunek jeste zgodny z osia preta. Moment M_s nazywany jest momentem skręcającym

Założenia

- przekrój płaski przed odkształceniem pozostaje płaski po odkształceniu

- nie ma odkształcenia w kierunku osi podłużnej pręta

- poszczególne przekroje tylko obracaj się względem osi podłużnej( względem przekroju sasidniego)

- materiał jest linowo sprężysty , obowiazuje prawo Hoocke'a

Podstawowe zależnośi

- warunki równowagi

- warunki geometryczne

- związki fizyczne ( równania konstytutywne)

Naprężenia styczne są proporcjonalne od odległości od srodka przekroju. Rozklad naprężeń w przekroju poprzecznym preta

- projektowanie

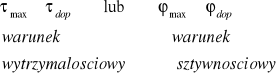
7. SKRECANIE OBLICZENIA WYTRZYMAŁOSCIOWE

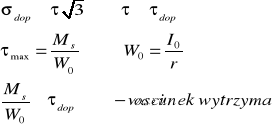
8. ZGINANIE PROSTE PRETOW. ZAŁOŻENIA. PODSTAWOWE ZALEŻNOŚCI.

Założenia

- belka jest obciazona momentem gnacym lub silami poprzecznymi ( prostopadłymi do osi podłużnej , skupionymi lub rozłożonymi w sposób ciągły) wywołującymi moment gnący

- przekrój plaski przed odkształceniem pozostaje płaski po odkształceniu

- belki traktujemy jako zbior warstw ( włókien) ulegających skróceniu ( ściskaniu) lub wydłużeniu (rozciąganiu)

- istnieje warstwa obojetna która nie ulega odkształceniu.

- naprężenia w warstwie obojętnej są równe 0

- materiał jest linowo sprężysty - obowiazuje prawo Hooke'a

WARUNKI ROWNOWAGI

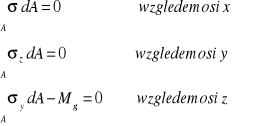
WARUNKI GEOMETRYCZNE

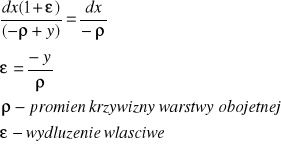
ZWIAZKI FIZYCZNE ( prawa konstytutywne )

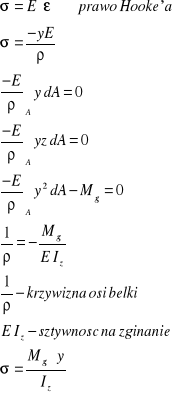
PROJEKTOWANIE

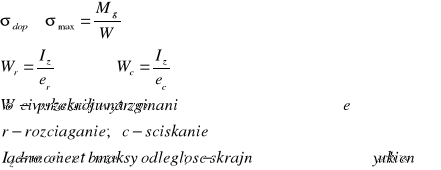
9. ZGINANIE PROSTE PRETÓW - OBLICZENIA WYTRZYMAŁOŚCIOWE

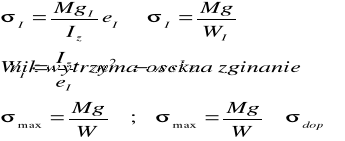
10. RÓWNANIE RÓZNICZKOWE OSI UGIETEJ

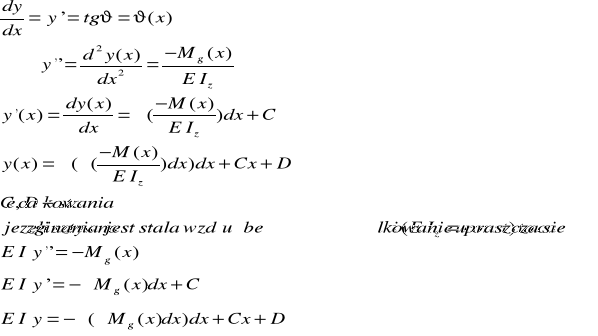
11. metoda clebscha - przyklad

12. Naprężenia w punkcie zależne od orientacji punktu.

Wartość napr. w punkcie dowolnego przekroju ( równanie w postaci wektorowej) wynosi:

Pu = Px l + Py m + Pz n

l, m, n- cosinusy kierunkowe normalnej n

Składowe naprężenia:

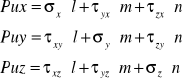
Naprężenie normalne wynosi

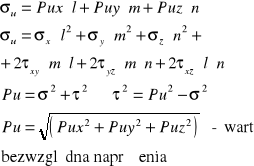
13. Składowe tensora stanu naprężenia.

Składowe tensora naprężenia.

Wielkość określona 3 wektorami -
, która przy zmianie układu osi transformuje się według formuł:

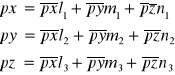
nazywamy tensorem.

- wektory stanu naprężenia

Tensor też może być określany składowymi algebraicznymi:

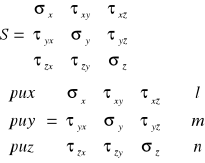
Dowolny tensor możemy rozbić na aksjator (część kulistą) i dewiator.

S=S_K+S_D S_K- tensor kulisty

S_D- dewiator

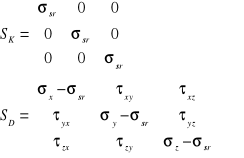
14. Równania równowagi stanu naprężenia.

Układając równania równowagi rozpatrujemy punkt obciążony siłami zewnętrznymi o wartościach x,y,z, oraz punkt w odległości nieskończenie małej od poprzedniego. Naprężenia składowe rozwijamy w szereg Taylora i po uproszczeniu otrzymamy:

15. Naprężenia główne i kierunki główne w ogólnym stanie naprężenia

Kierunki główne: określone przez oś u dla którego naprężenie styczne jest równe 0. Wtedy napr. normalne jest napr. całkowitym i nazywamy je napr. głównym

Płaszczyzna główna: pł. na której występuje naprężenie główne.

Na kierunku głównym zachodzi zależność

Pux = σ l ; Puy = σ m ; Puz = σ n

Równanie sekularne : σ³-σ²s₁+σs₂-s₃ = 0 ; do wyznacznia naprężeń głównych σ₁>σ₂> σ₃

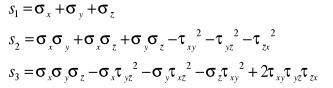
Niezmienniki stanu naprężenia: kier. główne, napr. główne, współczynniki s₁, s₂ , s₃

S_I, S_II, S_III - niezmienniki stanu naprężenia

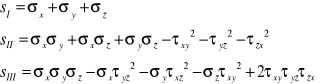
16. Szczególne przypadki stanu naprężenia

1.Przestrzenne nierównomierne rozciąganie:

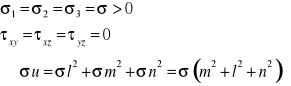
σ _u=σ -> naprężenie normalne na dowolnej płaszczyźnie niezależne od orientacji.

Naprężenie całkowite Pu=σ , wtedy τ_u=0 napr styczne

Koła Mohra to punkty.

2.Płaskie równomierne rozciąganie

zał. σ₁=σ₂=σ>0 σ₃=0

σ_u=σ - napr. normalne

τ_u=0 - napr. styczne

3.Jednoosiowe rozci*ganie

σ₁=σ>0 σ₂=σ₃=0 σ_x=σ σ_y=0 τ_xy=0

Naprężenia dla dowolnie zorientowanej płaszczyzny wynoszą:

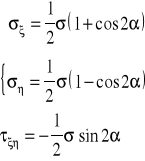
gdy: α=45° wtedy σ_ξ=σ_η=¹/₂σ

τ_ξη=τ_ξηmax=-¹/₂σ

4.Ścinanie

σ₁=σ σ₂=-σ σ₃=0

Napr. dla dowolnej płaszczyzny

σ_ξ=σ cos2α

σ_η=-σ cos2α

τ_ξη=-σ sin2α

Dla α=45°⇒ τ_ξη=τ_ξηmax=-σ oraz σ_η=σ_ξ=0

17.Płaski stan naprężenia: gdy σ₁≠0, σ₂≠0, σ₃=0 Płaski stan napr. opisany jest 3 składowymi σ_x , σ_y , τ_xy=τ_yx Równanie sekularne (jest funkcją kwadratową)

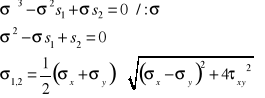
18. Teoria stanu odkszatałcenia

Pręt obciążony ulega przemieszczeniu (jego końce). Przemieszczenia końców pręta rozwijamy w szereg Taylora:

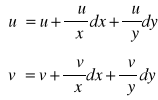
u, u' przemieszczenie względem OX

v, v' przemieszczenie wzgledem OY

19. Tensor stanu odkształcenia

T=T_K+T_D

T_K - tensor kulisty

T_D - dewiator

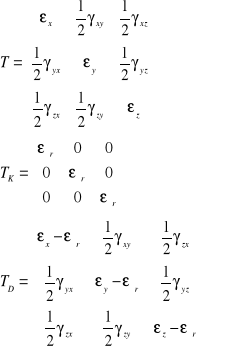
20. Odkształcenie główne i kierunkowe główne

Kierunki główne - kierunki w których odkształcenia postaciowe są równe 0 ( γ=0)

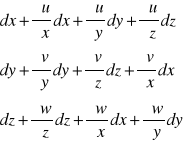
Dla każdego stanu odkształcenia można wyznaczyć 3 wzajemnie prostopadłe osie o kierunkach zwanych głównymi kierunkami stanu odkształcenia, dla których posunięcia będą równe zero.

Odkształcenia główne - odkształcenia ε_x, ε_y, ε_z na kierunkach głównych.

Niezmienniki stanu odkształcenia e₁, e₂, e₃

ε³ - ε²e₁ + e₂ - e₃ = 0

e₁ = ε_x + ε_y + ε_z

e₂ = ε_x ε_y + ε_yε_z + ε_zε_x - (1/4)(γ²_xy + γ²_yz + γ²_zx )

e₃ = ε_xε_yε_z + (1/4)( γ_xyγ_yzγ_zx ) - (1/4)( ε_xγ²_yz + ε_yγ²_zx + ε_zγ²_xy)

21 . Uogólnione prawo Hooke'a.

-Uogólniony związek pomiędzy stanem naprężenia i odkształcenia.

Określamy związki pomiędzy E, G i υ

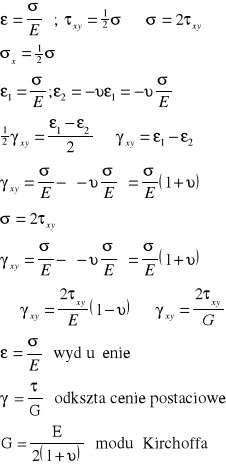
-Stała materiałowa dla ciała izotropowego.

Dla materiałów izotropowych uogólnione prawo Hooke'a wygl*da następuj*co:

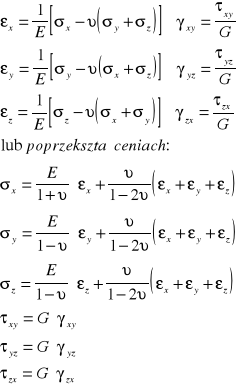
Kierunki główne stanu odkształcenia pokrywaj* się z kierunkami głównymi stanu naprężenia.

Stała Lame'go:

ν - liczba Poissona

G - moduł Kirchoffa

22. Moduł ściśliwości sprężystej

P=b_śr/e - względna zmiana objętości

23. Dewiator i część kulista tensora stanu naprężenia i odkształcenia.

Dewiator to taki tensor 2giego rzędu dla którego suma elementów głównych przekątnych jest równa zero.

Z dowolnego tensora stanu naprężenia
zawsze można wyodrębnić tensor kulisty

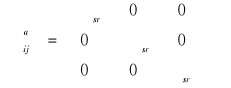
albo

24. Energia sprężysta

Zasadę energii mówiącą o równości przyrostu energii kinetyczne ciała i pracy sił na to ciało działających należy wyrazić uwzględniając zarówno siły zewnętrzne jak i wewnętrzne.

E - przyrost energii kinetycznej

L - praca sił zew.

A - praca sił wew.

Praca sił wew. w materiale sprężystym jest odwracalna i określa się ją jako energie potencjalną wew. sił sprężystych lub krócej energią sprężystą

A = - V

ΔE+V=L

Energia sprężysta w stanie nie naprężonym i nie odkształcalnym jest równa zero. Ponieważ energię sprężystą obliczać będziemy dla stanu równowagi, wiec ΔE = 0 wówczas V = L

V - całkowita energia pręta

AL. - objętość pręta

25. Układy liniowo sprężyste

Układ sprężysty zdeformowany działaniem sił, po odciążeniu powraca do swoich poprzednich kształtów i wymiarów. Jeżeli przemieszczenie Δ dowolnego pk. układu wywołane zrównoważonym działaniem sił zew. P₁, P₂, ......P_n da się wyrazić jako funkcje liniową tych sił

Δ=
to taki układ nazywamy liniowo sprężystym lub układem Clapeyrona. Współczynniki
określają wpływ jaki wywiera odpowiednia siła na przemieszczenie sprężyste Δ, nazywamy je liczbami wpływowymi przemieszczeń sprężystych. Wartości ich zależne są od kształtu i rozmiaru układu, od miejsca odniesienia sił, od sprężystych własności samego materiału, a nie są zależne od wartości siły. Aby układ można było uważać za liniowo sprężysty musi on spełniać następujące warunki:

1. marteriał musi być liniowo - sprężysty

2. układ jest w równowadze

3. brak tarcia na powierzchniach styku wzajemnie ruchomych części układu

4. przemieszczenia są tak małe, że nie wpływają w sposób godny uwzględnienia na skutki działania sił.
   
   
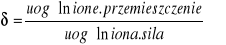
   Liczby wpływowe można uznać za przemieszczenie wywołane odpowiednimi siłami o wartości jeden
   26. Twierdzenie Betti'ego i Maxwella

-Tw. Bettiego o wzajemności prac. Suma prac wirtualnych układów sił P­_i na odpowiadających na przemieszczeniach wywołanych przez układu sił P_j równa się sumie prac wirtualnych układu sił P_j na przemieszczeniach wywołanych układu sił P_i.

Tw. Maxwella o wzajemności przemieszczeń. Przemieszczenie pkt. Zaczepienia siły P_i wywołane przez siłę P_j i zrzutowane na kierunek działania siły P_i oraz przemieszczenie pk. zaczepienia siły P_i i zrzutowane na kierunek działania siły P_j są sobie równe, jeżeli P_i=P_j

27. Twierdzenie Castigliano i Menabrea - Castigliano

-Tw. Castigliano i jego zast. w obliczaniu przemieszczeń. Pochodna cząstkowa całkowitej energii sprężystej układu liniowo sprężystego względem siły ogólnejdziałającej w danym pkt. równe jest przemieszczeniu tego pkt. W kierunku działającej siły.

żnak + zwrot zgodny z kierunkiem działania siły, znak - niezgodny z kierunkiem działającej siły.

Tw. Menabrea - Castigliano.

W układzie liniowo sprężystym sztywnie podpartym pochodna cząstkowa energii sprężystej całego układu względem wielkości podporowej - hiper statycznej jest równa zero.

28. Metoda Maxwella-Mohra

Twierdzenie Maxwella-Mohra .

Uogólnieone przemieszczenie f_i wynosi
Fi - uogólniona siła Fi

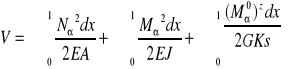
energia sprężysta

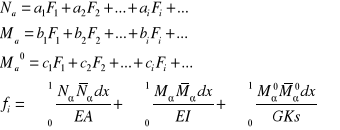
wzór Maxwela Mohra

siły wewnętrzne

29. Wytężenie materiału. Hipotezy wytężeniowe

Pojęcie wytężenia materiału.

Ogół zmian w stanie fizycznym ciała prowadzący do powstania trwałych odkształceń i zniszczenia spójności określono jako wytężenie. Stawia się hipotezę, że można utworzyć funkcję W określającą wytężenie. Jej argumentem są składowe stanu ośrodka ciągłego w danym punkcie (z reguły składowe stanu naprężenia σ_X , ..., τ_XY , ...) i parametry charakteryzujące materiał (C₁,...)

W=F(σ_X , ..., τ_XY ,...,C₁ ,...)

Naprężenie redukowane.

Naprężenie zredukowane odpowiada danemu stanowi naprężenia i jest porównywalne z jednokierunkowym stanem naprężenia.

Wytężenie to zagadnienie odpowiedności trój- lub dwukierunkowego stanu naprężenia z jednokierunkowym stanem naprężenia.

Hipotezy wytężenia.

1)Hipoteza największego naprężenia normalnego (Galileusz i Leibnitz). O wytężeniu decyduje max. naprężenie normalne (rozciągające lub ściskające)

a) Przestrzenny stan naprężenia.

σ₁ <= σ_zr , σ₂ <= σ_zr , σ₃ <= σ_zr

σ_zc <= σ₁ <= σ_zr , σ_zc <= σ₂ <= σ_{zr ,}

σ_zc <= σ₃ <= σ_zr

b)Płaski stan naprężenia σ₃ = 0

σ_zc <= σ₁ <= σ_{zr ,}

σ_zc <= σ₂ <= σ_zr

c)Ścinanie

τ_max = σ

σ_zc <= τ_max <= σ_zr

2)Hipoteza najwiekszych odkształceń właściwych (de Saint-Vermont)

O wytężeniu decydują odkształcenia (wydłużenie właściwe)

ε₁ <= ε_zr , ε₂ <= ε_zr , ε₃ <= ε_zr , ε_zc <= ε₁ <= ε_zr

3)Hipoteza największych naprężeń stycznych

O wytężeniu decyduje

max. naprężenie

styczne

τ_max = (σ_max - σ_min) /2

a)Rozciąganie osiowe - τ_max = σ_red /2

b)Ogólny stan naprężenia - σ_red = σ_max - σ_min

-σ_zr <= σ_max - σ_min <= σ_zr

-σ_zr <= σ₁ - σ₂ <= σ_zr

-σ_zr <= σ₂ - σ₃ <= σ_zr

c)Płaski stan naprężenia - σ₃ = 0

-σ_zr <= σ_max - σ_min <= σ_zr

- różne znaki σ_x , σ_y

σ_x σ_y <= τ_xy²

- te same znaki σ_x , σ_y

σ_x σ_y > τ_xy²

Szczególne przypadki:

I) σ_x = σ , σ_y = 0 , τ_xy = τ →

II)Ścinanie

τ_xy = τ , σ_x = 0 , σ_y = 0 →

4)Hipoteza energetyczna

a)Miara wytężenia - całkowita energia sprężysta (Huber,Beltrami)

b)Miara wytężenia - energia odkształcenia postaciowego (Huber,Ses)

Dla dowolnego stanu naprężenia spowodowanego rozciąganiem:

Φ_f = (1+ν) /6E [(σ_x -σ_y)²+(σ_y -σ_z)²+(σ_z -σ_x)²+

+6(τ_xy² +τ_yz² +τ_zx²)]-energia odkszt.postac.

Dla płaskiego stanu naprężeń: σ_z = τ_yz = τ_zx = 0

Szczególne przypadki:

I) σ_x = σ , σ_y = 0 , τ_xy = τ ,

II) Ścinanie: σ_x ,σ_y = 0 , τ_xy = τ ,

30. HIPOTEZA NAJWIĘKSZYCH NAPRĘŻEŃ STYCZNYCH

(Tresci i de Saint Venanta)

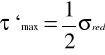
31. UOGÓLNIENIE MOHRA HIPOTEZY NAJWIĘKSZYCH NAPRĘŻEŃ STYCZNYCH !!!

32. HIPOTEZY ENERGETYCZNE. HIPOTEZA ENREGII ODKSZTAŁCENIA

POSTACIOWEGO

(Hubera - Misesa)

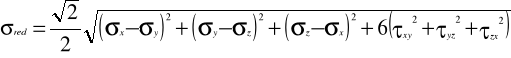
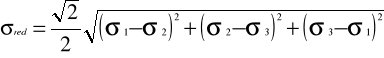
33. ZGINANIE UKOŚNE

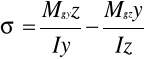
jeżeli

to

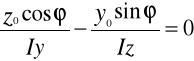
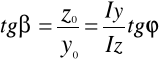
34. ŚCINANIE. WZÓR ŻURAWSKIEGO

Naprężenia normalne w dowolnym przekroju wyznacza się jak w prostym zginaniu równomiernym

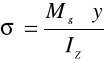
W przekroju przesuniętym względem poprzedniego o dx moment gnący wzrośnie o dM_g a naprężenie normalne o dσ.

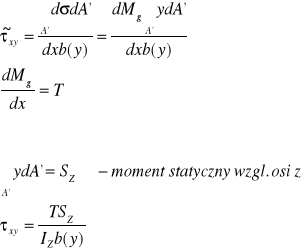
Wzór Żurawskiego pozwala obliczyć w sposób przybliżony wartość jednej składowej τ_XY naprężeń stycznych w przekroju pręta zginanego nierównomiernie.

Środek ścinania.

K - środek ścinania (jeżeli w punkcie k przyłożymy siłę skupioną to nastąpi tylko zginanie bez skręcania)

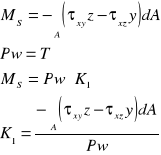
Wpływ sił poprzecznych na przemieszczenie osi pręta.

Na osi pręta przemieszczenie υ jest równe ugięciu y zależnemu tylko od x

różniczkując jednokrotnie wzgl. x mamy:

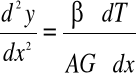
Równania te można uważać za równania różniczkowe osi odkształconej działaniem sił poprzecznych. Takie ujęcie pozwala nam wnieść poprawkę do równania różniczkowego osi ugiętej, które po uwzględnieniu działania sił poprzecznych przybiera postać:

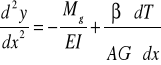
35. ROZCIĄGANIE ZE ZGINANIEM

Siły wewnętrzne w przekroju :
- siła normalna

- moment gnący

Moment gnący nie pokrywa się z żadną z głównych centralnych osi bezwładności przekroju, czyli jest to zginanie ukośne. Wektor momentu rozkłada się na dwie składowe

,

Naprężenia można wyznaczyć na podstawie superpozycji z zależności

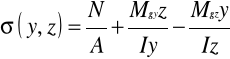
W trakcie odkształcenia pręta jego przekrój dokonuje obrotu wokół osi y oraz z i przemieszcza się w kierunku osi x. Ślad przecięcia się płaszczyzn przekroju po i przed odkształceniem wyznacza linię obojętną. Jest to miejsce geometryczne punktów przekroju, w których naprężenie normalne równa się zero.

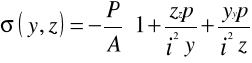
oraz
i
w celu wyróżnienia punktów przekroju należących do linii obojętnej

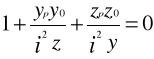
gdzie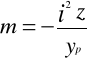
,
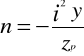
odcinki odcięte przez linię obojętną na osiach y i z

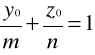
36. RDZEŃ PRZEKROJU

Zbiór punktów przyłożenia siły odpowiadających wszystkim liniom obojętnym stycznym do konturu przekroju pręta ogranicza obszar zwany rdzeniem przekroju.

Jest to miejsce geometryczne punktów przyłożenia siły, dla których naprężenia w całym przekroju mają jednakowy znak.

37. ZGINANIE ZE SKRĘCANIEM

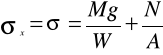
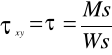
naprężenia redukowane :

- hipoteza maksymalnych naprężeń stycznych

- hipoteza energii odkształcenia postaciowego

gdy N=0 rozpatrujemy zginanie ze skręcaniem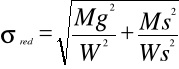

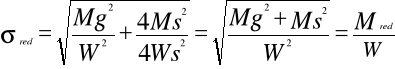
dla przekroju kołowego Ws=2W

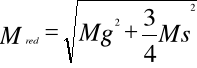
38. WYBOCZENIE SPRĘŻYSTE PRĘTÓW - WZÓR EULERA

Wyboczenie to wyginanie pręta spowodowane przekroczeniem przez siłę ściskającą wartości krytycznej.

Siła krytyczna Eulera:

P_kr = n²Π²EI / l² (Wyboczenie sprężyste)

Dla n=1 P_kr = Π²EI / l². EI -sztywność pręta;

n -ilość półfal sinusoidy krzywej ugięcia pręta

Siła krytyczna -najmniejsza siła po przekroczeniu której pręt utraci stateczność.

Końcowy wzór Eulera:

P_kr = Π²EI / l_r² [l_r=αl, α-wsp. zależny od sposobu zamocowania (0,5do2).

Krzywa ugięcia pręta: y=Asin(πx/2), dla P=P_kr jest półfalą sinusoidy.

α=2 - P_kr/min, α=1/2 - P_kr/max

Naprężenie krytyczne:

σ_kr=P_kr /A → σ_kr=Π²EI / l_r²A

Promień bezwładności: i²=I /A,

Smukłość pręta: λ=l_r /i

Ostateczny wzór w zakresie wyboczenia sprężystego na napr. krytyczne (w zakresie stosowania prawa Hooke'a): σ_kr=Π²E /λ²

Graniczna wartość smukłości:

σ_kr=δ_H →Π²E /λ²=δ_H →λ_gr= Π

Wyboczenie niesprężyste.

Naprężenia krytyczne wyznaczamy.

Dla λ<λ_gr ze wzorów empirycznych:

a) - Tetmajera-Jasińskiego: σ_kr = a-bλ,

b) - Johnsona-Ostanfelda: σ_kr = A-Bλ²,

a ,b, A, B - stałe materiałowe.

39. WYBOCZENIE SPRĘŻYSTO - PLASTYCZNE PRĘTÓW - RODZAJE APROKSYMACJI

40. ZAGADNIENIA BRZEGOWE TEORII SPRĘŻYSTOŚCI. SFORMUŁOWANIE, SPOSÓB

ROZWIĄZANIA

Podstawowe równania teorii sprężystości.

1. Warunki równowagi:

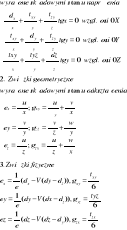
Równania ciągłości odkształceń (nierozdzielności odkształceń)

Wyrażenia określające związki geometryczne różniczkujemy obustronnie wzgl. x,y,z, sumujemy i otrzymujemy 6 równań nierozdzielności odkształceń

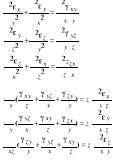
Równania przemieszczeniowe teorii sprężystości (Naviera-Lamego).

Wyrażając naprężenia za pomocą składowych stanu odkształcenia, równania równowagi wyrażamy za pomocą przemieszczeń. Równania takie nazywamy równaniami Lamego:

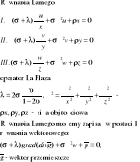
Równania naprężeniowe (Beltromiego - Michela).

Rozpatrujemy w płaskim stanie naprężenia element w kształcie pierścienia.

Pa,Pb - ciśnienie, które powoduje, że element przemieszcza się.

Rozpatrujemy nieskończenie mały wycinek pierścienia

r-promień, σ_r -naprężenie obwodowe, A', B', C' - punkty wycinka po przemieszczeniu

Rozpatrując siły na oś y otrzymujemy:

Równanie osi pionowej możemy przedstawić za pomocą przemieszczeń

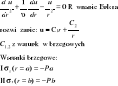
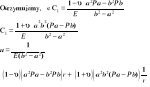
41. Podstawy metody elementów skończonych. Założenia. Podstawowe zależności

Dyskretyzacja pręta za pomocą elementów skończonych.

MES jest to metoda ogólnie stosowanej mechaniki ośrodków odkształcalnych. Punktem wyjścia metody jest koncepcja zastąpienia ośrodka ciągłego układem dyskretnych elementów skończonych. Relacje jakie w układzie takim powinny być spełnione zapisuje się w postaci równań macierzowych a ich rozwiązanie jest możliwe jedynie za pomocą komputera. Podstawą rozwiązania zagadnienia układu liniowo sprężystego metodą MES jest równanie macierzowe: P=AU formułujące związki liniowe między przemieszczeniami U, a siłami P zdeterminowane przez macierz sztywności A.

Aproksymacja przemieszczeń za pomocą funkcji interpolacyjnych (f. Kształtu), całka ważona, sformułowanie słabe.

W metodzie elem. skończ. w ujęci Raybigha - Ridsa podstawowe równania metody wyprowadzamy ze sformułowania słabego przyjmując przybliżenie oraz zakładając że funkcja ważona w(e) wyrażona jest przez funkcję kształtu: W=N^e₁ , W=N^e₂ , W=N^e₃ , W=N^e₄ .

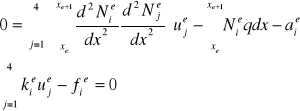
Otrzymuje się:

Macierz sztywności elementu skończonego

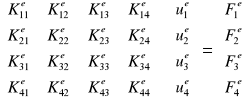
Macierz [K^e] jest macierzą sztywności elementu belkowego, natomiast macierz [F^e] jest macierzą kolumnową sił.

Agregacja elementów skończonych (warunki zgodności przemieszczeń i równowagi sił).

Jeżeli rozważany element skończony Ω^e wstawimy do jego pierwotnego miejsca w pręcie to powinny być spełnione dwa następujące warunki: warunek zgodności przemieszczeń w węźle u^e₂ = u^e+1₁ = u_e+1 , warunek równowagi sił w węźle a^e₂ ÷ a^e+1₁ ={0 gdy w węźle nie działają siły zewnętrzne, a₀ gdy w węźle działa siła skupiona o wartości a₀}.

42 i 43 . Elementy prętowe rozciągane i skręcane MES

dla 0<x<l

które należy uzupełnić warunkami brzegowymi u(0)=u₀ ; (adu/dx)_x=l = a₀ gdzie a=a(x)=A(x)*E jest sztywnością na rozciąganie.

26

Mg

y'(x)

x

x

y

s

b

a

x

y

A

dA

d

b

a

c

x

y

x

y

dA

A

y

x

x

y

---