1.Co to jest równowaga względna
Jest to stan w którym jednocześnie prędkość względna i przyspieszenie względne są równe 0.
* )![]()
,![]()
W stanie równowagi względnej pkt mat jest unieruchomiony w układzie unoszenia
Warunek istnienia tego stanu przy *)
![]()
(-mpu)- siła bezwładności unoszenia
2.Przyspieszenie Coriolisa
Jest to przyspieszenie wynikające z ruchu unoszenia. ![]()
Jest równe podwojonemu iloczynowi wektorowemu prędkości kątowej i prędkości względnej, jest prostopadłe do wektorów ω i w i długości i zwrocie takim że wektory tworzą układ prawoskrętny jak układ osi (x,y,z) ![]()
gdzie ![]()
kąt między wektorami w i ω. PC jest równe 0 gdy: (1) ruch unoszenia jest postępowy ω=0, (2) w pewnej chwili prędkość względna punktu jest równa 0 w=0, (3) wektor prędkość względna pktu jest równoległy do wektora prędkości kątowej PC występuje gdy układ unoszenia dokonuje obrotu. Występuje, gdy punkt znajduje się w początku ruchomego układu wsp. Np. ruch obrotowy ziemi powoduje powstawanie przyspieszenia Coriolisa.
3.Przyspieszenie unoszenia w ruchu złożonym pkt mat
Jest to przyspieszenie punktu układu unoszenia w którym aktualnie znajduje się punkt poruszający się ruchem złożonym.
![]()
Składa się przysp pkt ruchomego , stycznego (obrotowe) i normalnego (doosiowe)
4.Równanie dynamiki ruchu względnego pkt mat
Równanie te wyprowadza się z II prawa Newtona o ogólnej postaci: F siła czynna, R reakcje więzów, mp przysp bezwzg.
![]()
![]()
![]()
-mpU -siła bezwładności unoszenia
-mpC -siła bezwładności Coriolisa.
5.Uderzenie pktu mat o przegrodę
Punkt uderza o powierzchnię przegrody będącej w spoczynku z prędkością v1 której kierunek tworzy kąt α (padania) z normalną do powierzchni przegrody. Po uderzeniu punkt odbija się i porusza się z prędkością v2 tworząc kąt β (odbicia) z normalną do pow przegrody. W trakcie zderzenia wystąpi reakcja mająca charakter siły zderzeniowej
mv2cosβ + mv2cosα = JRn
mv1sinβ - mv1sinα = -JRt
J - impuls reakcji normalnej.
Są cztery niewiadome więc dobieramy 2 równania z hipotezy impulsu stycznego JRt=0 i hipotezy restytucji normalnej.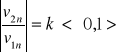
Stosunek bezwzględnych współrzędnych wartości normalnych składowych prędkości po i przed zderzeniem i jest niezależny od tego z jaką prędkością pkt uderza.
6.Określenie współczynnika restytucji przy zderzeniu dwóch kul
v1,v2-prędkości przed zderzeniem
w1,w2-prędkości po zderzeniu
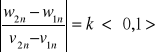
7.Wpływ siły impulsowej na ruch punktu materialnego
Skutkiem działania na pkt impulsu siły jest skończona zmiana prędkości (wartości i kierunku).![]()
8.Wpływ siły impulsowej na ruch ciała sztywnego
Ruch ten bada się za pomocą praw zmienności pędu i krętu.
Powoduje sokową zmianę wektora prędkości środka masy oraz środkową zmianę wektora prędkości kątowej.
9.Środek uderzenia
Jest to punkt bryły spełniający warunki: 1) impuls uderzenia J powinien być _|_ do płaszczyzny utworzonej przez oś obrotu i środek masy bryły, 2)oś obrotu powinna być osią główną bryły w pkt będącym rzutem pkt uderzenia na oś obrotu bryły, 3) odległość pkt uderzenia od osi obrotu powinna spełniać warunek ZB=IY/(mZC)
10.Zmiana energii kinetycznej pktu mat przy uderzeniu o przegrodę
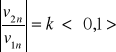
Różnica energii kinetycznej po i przed zderzeniem wynosi Ek2-Ek1= ΔEk
Następuje więc ubytek energii kin tym większy im mniejszy jest współ restytucji. W przypadku zderzenia plastycznego cała energia kin zostaje stracona. W przypadku uderzenia idealnie sprężystego nie ma straty energii. W przypadku częściowo sprężystego zderzenia część energii kin zostaje stracona, zamienia się w ciepło.
11.Energia kinetyczna ciała sztywnego
![]()
Wielkości potrzebne do obliczenia EK bryły sa: prędkość pewnego jej pkt (va),prędkość kątowa(ω),położenie środka masy względem pkt o znanej prędkości (pC),masa (m) i momenty bezwładności i dewiacji. Rozpatrujemy teraz przypadki:
1)gdy ω=0 to Ek=(mvA2)/2
2)gdy vA=0 to Ek=(Ilω2)/2
3)gdy pC=0 i vA=vC to
Ek=(mvC2)/2 +(ILCω2)/2
12.Twierdzenie Koeniga o energii kinetycznej ciała sztywnego.
Ek=(mvC2)/2 +(ILCω2)/2
m-masa, vC- prędkość środka masy, ω-prędkość kątowa, ILC- moment bezwł bryły względem osi przechodzącej przez środek masy i || do wektora ω
13.Niewyrównoważenie statyczne i dynamiczne ciała sztywnego.
W maszynach zawierających elementy wirujące występuje okresowa zmiana siły działającej na łożyska, co wywołuje drgania. Dynamiczne - występują gdy środek masy ciała wirującego nie leży na osi obrotu oraz oś ta nie jest osią główną, ponieważ przy wykonywaniu elementu nie zawsze da się to spełnić, więc każdy ele jest poddawany sprawdzeniu. Dodając lub odejmując masę można wpłynąć na położenie środka masy i rozkład momentów bezwładności - wyrównoważenie.
14.Reakcje dynamiczne w łożyskach wirującej bryły
Jeżeli środek masy ciała leży na osi obrotu i jednocześnie oś ta jest osią główną ciała dla dowolnego jej punktu to reakcje dynamiczne są równe 0. Reakcje dynamiczne występują, jeżeli środek masy ciała wirującego nie leży na osi obrotu oraz jeżeli oś ta nie jest osią główną. Do reakcji statycznych wynikających z obciążenia siłami dochodzą reakcje dynamiczne konieczne do utrzymania ciała w określonym ruchu obrotowym. Reakcje te wynikają ze zmian pędu i krętu ciała. Gdy oś obrotu nie przechodzi przez środek masy ciała występuje okresowa zmiana siły działającej na łożyska. Siła ta przenosząc się na elementy fundamentu wywołuje drgania.
15.Zjawisko giroskopowe
Giroskop jest to ciało mające kształt bryły obrotowej obracającej się szybko wokół swej osi symetrii z prędkością kątową ω2 A oś symetrii obraca się jeszcze z prędkością kątową ω1. Osie przechodzą przez środek masy w pkt A. Ciało wykonuje ruch kulisty i ruch ten jest precesją regularną. Dla wywołania ruchu przykładamy moment sił zewnętrznych MG. Zakładamy, że ω1 obrotu osi wirującej jest dużo mniejsza od ω2 obrotu własnego a więc kręt nie zależy od ω1 tylko od ω2 i leży na osi obrotu własnego. Giroskop dąży do zachowania położenia swej osi obrotu w przestrzeni. Stosowany w samolotach (sztuczny horyzont) statki (stabilizacja)
16.Równanie ruchu pkt mat o zmiennej masie
![]()
v-prędkość pkt, u- prędkość dołączającej się cząstki
17.Kiedy równanie ruchu pkt mat o zmiennej masie ma postać II prawa Newtona
Gdy prędkość względna dołączającej się masy jest równa zero w=0 Równanie ma formalnie postać identyczną z równaniem ruchu punktu o stałej masie, z tym że masa jest funkcją czasu.
![]()
18.Równanie Mieszczerskiego (ruch punktu o zmiennej masie)
![]()
Uogólniony wzór dla pkt nieswobodnego:
![]()
w=u-v
Równanie ma postać II prawa Newtona gdy w=0
19.Zasada prac wirtualnych
Pracą wirtualną dowolnej siły rzeczywistej ![]()
działającej na pkt mat nazywamy iloczyn skalarny siły i przemieszczenia wirtualnego tego pktu:![]()
Układ pktów mat jest w równowadze (wtedy i tylko wtedy) gdy suma prac sił zew czynnych, reakcji zew i sił wew w połączeniach podatnych na przemieszczeniach wirtualnych pktów układu = 0 ![]()
20.Określenie współrzędnych uogólnionych i sił uogólnionych dla układu pkt mat
Wsp uogólnione- niezależne wsp których liczba jest najmniejszą potrzebną do określenia położenia układu (3n-k) Mogą to być wsp kątowe bądź liniowe. Liczba wsp uogólnionych jest najmniejszą potrzebną do określenia położenia i ruchu. Min liczbę wsp potrzebną do określenia położenia układu nazywamy liczba stopni swobody S=3n-k. Siła uogólniona- wielkość, która pomnożona przez przyrost przygotowany wsp uogólnionej daje wartość pracy wykonanej przez układ sił działających na dany układ materialny na przesunięciach przygotowanych wywołanych przyrostem wsp uogólnionej Przyrost przygotowany
21.Zasada d'Alemberta -formułowanie, zastosowanie
![]()
Ruch układów pktów mat odbywa się w taki sposób, że suma prac wirtualnych sił zew, wew, i sił bezwładności na przemieszczeniach wirtualnych pomyślanych w dowolnej chwili podczas ruch jest = 0.
22.Określenie przemieszczenia wirtualnego (przygotowanego)
Przesunięciem przygotowanym nazywamy takie dowolnie pomyślane przez obserwatora przesunięcie będące jednym z przesunięć możliwych niezwiązane ani z działającymi siłami ani z czasem. Jeżeli na punkt materialny działa siła Fi to po nadaniu punktom przesunięcia przygotowanego δri zostanie wykonana praca elementarna ![]()
23.Określenie zderzenia prostego, ukośnego, centralnego i niecentralnego
Przy zderzeniu dwóch ciał powierzchnie tych ciał zetkną się w jednym punkcie. Punkt A I ciała zetknął się z punktem D II ciała. Powierzchnie tych ciał w punkcie zetknięcia mają wspólną normalną (linia zderzenia). Prędkość względna punktu A w stosunku do punktu D jest równa i przeciwna prędkości względnej punktu D w stosunku do punktu A. Jeżeli te prędkości względne są położone na linii zderzenia to zderzenie nazywamy prostym w przeciwnym razie ukośnym. Przy zderzeniu prostym siły chwilowe działają na linii zderzenia. Jeżeli linia zderzenia przechodzi przez środek masy ciała to zderzenie nazywamy centralnym w odróżnieniu od zderzenia mimośrodowego w przypadku przeciwnym.
24.Zderzenie dwóch kul
Zakładamy, że dwie kule o masach m1 i m2 poruszają się ruchem postępowym z prędkościami v1 i v2 przed zderzeniem tak, że torem środka masy każdej jest prosta, na której znajdują się ich środki O1 i O2. Aby zderzenie było możliwe v1- v2>0. Rzut wektora pędu na oś x wobec braku sił zewnętrznych jest stały. Po uderzeniu kule zaczną poruszać się z prędkościami w1 i w2 skierowanymi także wzdłuż osi x. Stałość pędu oznacza, że pęd układu po i przed zderzeniem jest taki sam ![]()
Stosunek prędkości względnych obu kul po i przed zderzeniem jest równy współczynnikowi restytucji 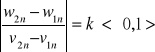
Przy zderzeniu plastycznym k=0 przy idealnie sprężystym k=1.
25.Co to jest ruch kulisty bryły; ruch kulisty regularny, precesja regularna
Ruch kulisty ciała sztywnego występuje, gdy jeden z punktów układy związanego z ciałem jest nieruchomy. Precesja regularna jest to szczególny przypadek ruchu kulistego ciała, w którym kat nutacji jest stały ϑ=const i prędkości kątowe obrotu własnego i precesji są stałe ω=const, Ruch ten cechuje się tym, że ciało obraca się wokół osi własnej ζ z prędkością kątową ω1 a oś ta obraca się wokół osi stałej z z prędkością kątową ω2. Kąt między osiami jest stały
27.Równanie ruchu rakiety
Ruch rakiety w czasie działania silnika rakietowego jest ruchem ciała o zmiennej masie, podczas którego następuje wypływ gazów spalinowych z dyszy silnika z prędkością względną uzyskiwaną w wyniku spalania paliwa. Zakładamy, że efektywna prędkość wypływu gazów jest stała ve ![]()
28.Równania ruchu ciała sztywnego
Prawo zmienności pędu i krętu są równaniami opisującymi ruch bryły w dowolnym jego przypadku
![]()
![]()
29.Równania Lagrange'a II rodzaju-sformułowanie, zastosowanie
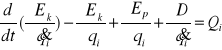
Są to równania różniczkowe zwyczajne II rzędu. Rozwiązanie tych równań stanowi najkrótszy sposób badania ruchu. Liczba równań różniczkowych jest przy tej metodzie najmniejsza i równa liczbie stopni swobody układu q.
30.Równania Lagrange'a w przypadku sił potencjalnych
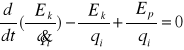
32.Równania dynamiki toczącego się koła
Równania dynamiki koła mają postać
![]()
,![]()
![]()
Ponieważ są 4 niewiadome musimy znaleźć zależność
1) p=εr - zal kinematyczna toczenie bez poślizgu
2) T=μN - zal silowa toczenie z poślizgiem
33.Równania ruchu pojazdu
mp=T1-T2-Qsinα -FU
N1+N2-Qsinα =0
![]()
![]()
p2=ε2r2, p1=ε1r,1 lub T1=μN1
35.Dynamiczne równania Eulera dla bryły sztywnej
A'+(C-B) '+(A-C) '+(B-A)=M. A,B,C- rzuty krętów na główne osie bezwładności
36.Prawo ruchu środka masy układu pktów mat
Pęd układu punktów materialnych jest równy iloczynowi masy całkowitej układu i wektora prędkości środka masy.
![]()
Środek masy układu materialnego porusza się tak jak punkt materialny, w którym skupiona jest masa całego ciała i do której przyłożone są siły równe wektorom głównym sił zewnętrznych i reakcji działających na dany układ
![]()
37.Prawo zmienności pędu i prawo zmienności krętu układu pktów mat
Prawo zmienności pędu:
Pochodna wektora pędu układu mat względem czasu równa jest sumie geometrycznej sił zewnętrznych działających na wszystkie pkty układu
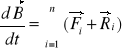
Krętem układu punktów materialnych względem punktu O w przestrzeni nazywamy wektor będący sumą geometryczną wektorów krętu wszystkich punktów układu, względem tego samego punktu O.
Prawo zmienności krętu:
Pochodna względem czasu krętu układu mat względem dowolnego stałego punktu równa jest sumie momentów wszystkich sił zewnętrznych działających na pkty układu względem tego samego pktu przestrzeni
![]()
38.Prawo zmienności energii układu pktów mat w potencjalnym polu sił
Przyrost energii kinetycznej układu = jest spadkowi potencjału
dEk=-dEp lub Ek + Ep = const
40.Równania dynamiki ruchu postępowego bryły
Ruch postępowy opisuje prawo zmienności pędu bryły
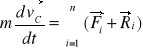
![]()
41.Równanie ruchu obrotowego bryły
Równanie ruchu obrotowego jest rzutem na kierunek osi obrotu równania wektorowego wyrażającego prawo zmienności krętu względem dowolnego pktu.
![]()
![]()
MAY -suma momentów względem osi obrotu wszystkich sił działających na bryłę
43.Opisz znane ci zasady mechaniki analitycznej
Zasady różniczkowe i całkowe. Obszar tej mechaniki nie jest precyzyjnie określony. Oprócz omówienia zasad mechaniki do mech analitycznej zalicza się rów ruchu zapisane za pomocą rów więzów, przesunięć i prac wirtualnych (przygotowanych). Należy więc zaliczyć do tej mechaniki rów Lagrange'a i Hamiltona.
44.Prawo zmienności pędu ciała sztywnego
Pochodna względem czasu wektora pędu bryły równa się sumie geometrycznej sił zew działających na bryłę.
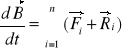
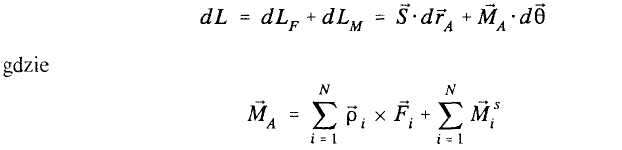
45.Prawo zmienności krętu ciała sztywnego
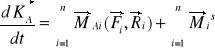
MAI-moment sił czynnych i reakcji
Mis - momenty swobodne
48.Pojęcie więzów układu mechanicznego i ich klasyfikacja
Układ, którego punkty nie mogą zajmować dowolnych położeń i mieć dowolnych prędkości niezależnie od działających sił nazywamy nieswobodnym. Na położenie i prędkości wszystkich lub niektórych punktów układu nałożone są warunki ograniczające ich swobodę zwane więzami. Więzy określone równaniami nazywają się więzami dwustronnymi, nierównościami jedno-stronnymi. Jeżeli równanie więzów zawiera tylko współrzędne punktów to nazywamy je więzami geometrycznymi. Równania więzów mogą być także zależne od prędkości punktów (więzy kinematyczne). Oba rodzaje więzów mogą być ponadto zależne od czasu (więzy niestacjonarne). Więzy niezależne od czasu- więzy stacjonarne. Więzy całkowalne są to więzy kinematyczne, które można przedstawić jako pochodną innej funkcji, która jest funkcją współrzędnych i czasu. Wtedy rów więzów kinematycznych może być zastąpione równoważnym rów więzów geometrycznych. Wieży idealne- są to więzy dwustronne, przy których suma prac przygotowanych i reakcji wywołanych tymi więzami na dowolnym przesunięciu przygotowanym jest równa 0.
49.Zdefiniować i podać przykład więzów nieholonomicznych
Są to więzy kinematyczne nie całkowalne
50.Wyznaczanie siły uogólnionej odpowiadającej danej współrzędnej uogólnionej w równaniach Lagrange'a (przykład)
Siłę uogólnioną można obliczyć jako pochodną potencjału względem odpowiedniej współrzędnej w przypadku gdy potencjał jest przedstawiony jako funkcja współrzędnych uogólnionych Qi=-Δv/Δqi. Niezależne współrzędne, których liczba jest najmniejszą potrzebną do określenia położenia układu nazywamy współrzędnymi uogólnionymi. Mogą być dowolnymi współrzędnymi liniowymi lub kątowymi. Siłą uogólnioną nazywamy taką wielkość, która pomnożona przez przyrost przygotowany δqj współrzędnej uogólnionej daje wartość pracy wykonanej przez układ sił działających na dany układ materialny na przesunięciach przygotowanych wywołanych przyrostem współrzędnej uogólnionej. Qj=δLj/δqj
51. Pęd układu punktów materialnych.
Pędem układu punktów materialnych nazywamy wektor, który jest sumą geometryczną wektorów pędów wszystkich punktów układu:
52. Energia kinetyczna układu punktów materialnych i prawo jej zmienności ?
Energią kinetyczną układu punktów materialnych nazywamy liczbę nieujemną będącą sumą energii kinetycznych wszystkich punktów układu:
Biorąc po uwagę, że suma prac sił wewnętrznych w połączeniach sztywnych jest równa 0, prawo zmienności energii kinetycznej układu zapiszemy w postaci:
Prawo to brzmi:
Elementarna zmiana energii kinetycznej układu punktów materialnych równa się sumie elementarnych prac sił zewnętrznych i sił wewnętrznych w połączeniach niesztywnych.
53.Prawo zmienności energii kinetycznej ciała sztywnego ?
Prawo to brzmi:
Elementarny przyrost energii kinetycznej ciała sztywnego równa się elementarnej pracy wykonanej przez siły i momenty swobodne działające na to ciało.
Łączna praca, jaką wykonują wszystkie oddziaływania mechaniczne momenty swobodne, wynosi:
Prawo zmienności energii kinetycznej ciała sztywnego ma postać:
dEk = dL
54.Równania ruchu ciała sztywnego wynikające z praw zmienności pędu i krętu ?
Prawo zmienności pędu (10.37) oraz prawo zmienności krętu bryły względem jej ruchomego punktu A są dwoma wektorowymi równaniami opisującymi ruch bryły w dowolnym jego przypadku. Przytoczmy je łącznie w postaci:
![]()
55.Dynamika bryły w ruchu postępowym ?
Przypomnijmy, że ruch postępowy to taki ruch bryły, w którym prędkość kątowa jest w sposób trwały równa zeru. Bryła w takim ruchu ma co najwyżej 3 stopnie swobody, którym mogą odpowiadać na przykład przemieszczenia środka masy C bryły w prostokątnym, nieruchomym układzie współrzędnych.
![]()
Ruch postępowy opisuje prawo zmienności pędu bryły, które możemy zapisać w postaci wektorowej
![]()
55. Dynamika bryły w ruchu kulistym.
Przypomnijmy,że ruch kulisty to taki ruch bryły, w którym jeden z punktów bryły lub przestrzeni z nią związanej pozostaje nieruchomy. Punkt ten nosi nazwę środka ruchu kulistego. Na bryłę w ruchu kulistym działają sił; czynne Ft, reakcja w środku ruchu kuliste go RA i, ewentualnie, moment Ms reprezentujący oddziaływania czynne w postać momentów swobodnych.
Prawa zmienności pędu i zmienności krętu w poruszającym się z bryłą układzie A, , przyjmują postać:
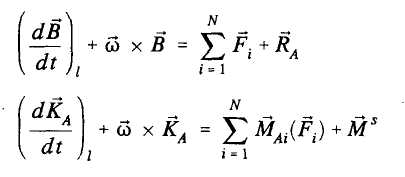
Wyszukiwarka