3. Stateczność prętów prostych, postacie utraty stateczności, metody określania sił krytycznych.

Konstrukcja znajduje się w stanie równowagi statycznej, jeśli po dowolnie małym odchyleniu od położenia pierwotnego konstrukcja wykazuje tendencje do powrotu do tego położenia pierwotnego. Utrata stateczności prowadzi do zniszczenia konstrukcji, gdyż pociąga za sobą duże odkształcenia i to w sposób nagły.

Aby konstrukcja znajdowała się w stanie równowagi statycznej muszą być spełnione warunki:

• konstrukcja musi być geometrycznie niezmienna

• obciążenie konstrukcji musi być mniejsze od P_kryt, przy którym następuje utrata stateczności

Stateczność prętów prostych

Występuje ono w przypadku działania na pręt siły osiowej S o tzw. wartości krytycznej S_kryt. Pręt znajduje się wówczas w stanie równowagi obojętnej; jego oś może pozostawać linią prostą, ale również nieskończenie mała dodatkowa przyczyna może wywołać jej wygięcie. Mówimy, że następuje wtedy wyboczenie pręta. Wartość krytyczną siły ściskającej dla swobodnie podpartego pręta o stałym przekroju poprzecznym wyznacza się na podstawie równania Euler'a:

w” + (SI²/EI)*w = 0

P_wyt = (Π²EI)/(μ*l²) - siła Eulerowska

Jeżeli smukłość rozważanego pręta jest większa od smukłości granicznej, to po osiągnięciu przez siłę S wartości krytycznej pręt ulega sprężystemu wyboczeniu.

Pręt ulegnie wyboczeniu przy dowolnej wartości obciążenia zewnętrznego.

W potocznym języku opór jaki stawia pręt zginany, przyjęto nazywać jego sztywnością.

Pręt rozciągany ma większą sztywność na zginanie niż pręt ściskany.

W przypadku gdy siła ściskająca ma wartość P_kr=Π²EI/(μ) sztywność pręta na zginanie jest równa 0.

Efekt polega na zmianie sztywności pręta na zginanie; ma to duże znaczenie w analizie statycznej złożonych ustrojów prętowych.

II.Postacie utraty stateczności:

Postać utraty stateczności zależy od przyłożonej siły oraz od geometrii ustroju

Stateczność

Pojedynczych prętów Układy złożone

Pręt idealny z imperfekcją idealny z imperfekcją

III.Metody określania sił krytycznych (zakres liniowo sprężysty)

* dla prętów prostych wzór Eulera P=Π²EI/l_w²

l_w - długość wyboczeniowa

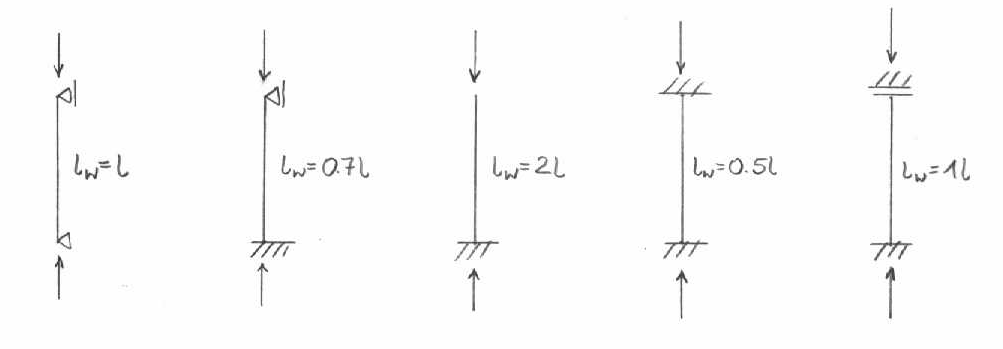
3. NAPRĘŻENIE NORMALNE W SŁUPIE

• średnie naprężenie ściskające

⇒

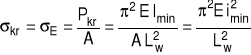
• zakres liniowo sprężystej ( LS )pracy materiału

• zakres pozaliniowo sprężystej pracy materiału

warunki „brzegowe”

aproksymacja liniowa T-J

aproksymacja paraboliczna J-O

4. PROJEKTOWANIE PRĘTÓW ŚCISKANYCH

• warunek projektowania
  

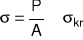
• W przypadku dopuszczenia do wyboczenia w zakresie pozaliniowo sprężystym przyjmuje się, że zamiast granicy plastyczności R_e należy wziąć wytrzymałość obliczeniową na rozciąganie R_o.

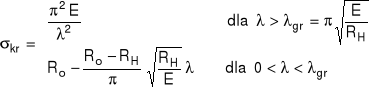
• założenie
  

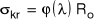
współczynnik wyboczeniowy

Normy uwzględniają we współczynniku wyboczeniowym takie czynniki jak losowość charakterystyk materiałowych, losowość obciążenia i odstępstwa od prostoliniowości pręta ściskanego (tzw. imperfekcje)

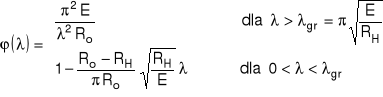
4.1. Algorytm obliczeń

1. warunek wytrzymałościowy
   

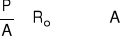
2. przyjąć przekrój
   

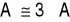
3. obliczyć smukłość pręta
   

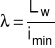
oraz tzw. smukłość porównawczą

4. z tablic wziąć wartość wsp. wyboczeniowego ϕ dla określonego stosunku
   

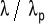
5. sprawdzić warunek projektowania
   

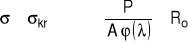
6. jeżeli warunek projektowania jest spełniony, to proces projektowania jest zakończony. W przeciwnym wypadku należy zwiększyć przekrój A' i wrócić do punktu 3.

II.Postacie utraty stateczności:

Postać utraty stateczności zależy od przyłożonej siły oraz od geometrii ustroju

• dla płaskich ustrojów ramowych: metoda przemieszczeń

Schemat postępowania:

1.Dobór układu podstawowego MP

2.Układ równań MP

3.Wyznaczenie współczynników- nowe wzory transformacyjne dla prętów obciążonych siłą osiową

1

równowaga

niestateczna

równowaga

obojętna

P ≅ P_kr

równowaga

stateczna

P > P_kr

P < P_kr

krzywa Eulera

aproks. Johnsona-Ostenfelda

aproks. Tetmajera-Jasińskiego

smukłość 

_gr

R_H

naprężenie krytyczne σ_E

wyboczenie poza

zakresem LS

wyboczenie w

zakresie LS

R_e

---