Akademia Górniczo - Hutnicza
w Krakowie
im St. Staszica.
Temat:
Próba statyczna rozciągania metali.
Wykonał:
Chudzikiewicz Marcin
Budownictwo rok II
Cel ćwiczenia.
Celem ćwiczenia jest zapoznanie ze sposobem przeprowadzenia próby statycznego rozciągania oraz ocena charakteru wykresu rozciągania.
Próba rozciągania należy do często stosowanych prób wytrzymałościowych.
Maszyna wytrzymałościowa.
Próba statyczna rozciągania wykonana została na maszynie wytrzymałościowej o napędzie mechanicznym. Siła rozciągająca odczytana została z wskaźnika zegarowego, wydłużenie próbki przymiaru liniowego, zaś urządzenie samopiszące wykonało wykres rozciągania. Jednostkowe wydłużenie odczytano z tensometru mechanicznego, który zamocowany został na próbce za pomocą dwóch pary ostrzy.
Wykres rozciągania.
Podczas rozciągania badaną próbkę poddaje się działaniu jednoosiowego obciążenia. Wykres zarejestrowany podczas próby na rejestratorze odwzorowuje przebieg rozciągania w układzie siła wydłużenie.
Na wykresie rozciągania można wyróżnić kilka podstawowych punktów:
Granica proporcjonalności. Jest to naprężenie, do którego występuje proporcjonalność naprężenia do wydłużenia jednostkowego.
![]()
[MPa]
Granica sprężystości. Zdefiniowano ją jako wartość naprężenia rozciągającego, które wywołuje wydłużenie trwałe równe 0,05% pierwotnej długości pomiarowej próbki.
![]()
[MPa]
Wyraźna granica plastyczności. Jest to naprężenie rozciągające, po osiągnięciu którego obserwuje się wyraźny wzrost rozciąganej próbki bez wzrostu obciążenia.
![]()
[MPa]
Umowna granica plastyczności. Określa się ją jako wartość naprężenia rozciągającego, które wywołuje w próbce wydłużenie trwałe równe 0.2% pierwotnej długości pomiarowej próbki.
![]()
[MPa]
Wytrzymałość na rozciąganie. Jest to naprężenie rozciągające, przy którym siła obciążająca uzyskuje maksymalną wartość.
![]()
[MPa]
Naprężenie rozrywające. Jest to naprężenie występujące w przekroju poprzecznym próbki w miejscu przewężenia, w chwili jej rozerwania.
![]()
[MPa]
Określenie własności plastycznych.
Do oceny własności plastycznych materiału, rozumianych jako zdolność do trwałych odkształceń, służy wydłużenie względne A10 oraz przewężenie względne Z.
![]()
[%]
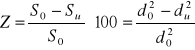
[%]
gdzie:
l0 - początkowa długość pomiarowa,
lu - długość pomiarowa po zerwaniu,
d0 - średnica początkowa próbki,
du - średnica próbki po próbie w miejscu zerwania.
Tok przeprowadzenia ćwiczenia.
Pomiar wymiarów próbki i umieszczenie jej w maszynie wytrzymałościowej.
Ustalenie znacznika na listwie pomiarowej.
Obciążanie próbki na napędzie ręcznym.
Odczytywanie wydłużenia jednostkowego z tensometru mechanicznego.
Odczytanie siły niszczącej, położenie znacznika względem listwy.
Opracowanie wyników.
Lp. |
Siła P [N] |
Wskazania czujników [10-2mm] |
Przyrosty [10-2mm] |
Wydłużenie Δl [mm] |
|||
|
|
l1 lewy |
l2 prawy |
Δl1 |
Δl2 |
|
|
1 |
1000 |
0 |
0 |
0 |
0 |
0 |
|
2 |
2000 |
0 |
0 |
0 |
0 |
0 |
|
3 |
3000 |
0 |
0 |
0 |
0 |
0 |
|
4 |
4000 |
0 |
1 |
0 |
1 |
0,005 |
|
5 |
5000 |
0 |
1 |
0 |
0 |
0 |
|
6 |
6000 |
0,1 |
1,2 |
0,1 |
0,2 |
0,0015 |
|
7 |
7000 |
0,1 |
1,8 |
0 |
0,6 |
0,003 |
|
8 |
8000 |
0,5 |
2 |
0,4 |
0,2 |
0,003 |
|
9 |
9000 |
0,5 |
2,5 |
0 |
0,5 |
0,0025 |
|
10 |
10000 |
0,9 |
3 |
0,4 |
0,5 |
0,0045 |
|
11 |
11000 |
1 |
3,5 |
0,1 |
0,5 |
0,003 |
|
12 |
12000 |
1,8 |
4 |
0,8 |
0,5 |
0,0065 |
|
13 |
13000 |
2,1 |
4,8 |
0,3 |
0,8 |
0,0055 |
|
14 |
14000 |
3 |
5,2 |
0,9 |
0,4 |
0,0065 |
|
15 |
15000 |
3,2 |
6 |
0,2 |
0,8 |
0,005 |
|
16 |
16000 |
4 |
6,7 |
0,8 |
0,7 |
0,0075 |
|
17 |
17000 |
4,8 |
7,2 |
0,8 |
0,5 |
0,0065 |
|
18 |
18000 |
5,1 |
8 |
0,3 |
0,8 |
0,0055 |
|
19 |
19000 |
6 |
8,7 |
0,9 |
0,7 |
0,008 |
|
20 |
20000 |
6,5 |
9,2 |
0,5 |
0,5 |
0,005 |
|
21 |
21000 |
7 |
10 |
0,5 |
0,8 |
0,0065 |
|
22 |
22000 |
7,5 |
10,7 |
0,5 |
0,7 |
0,006 |
|
23 |
23000 |
8 |
11,2 |
0,5 |
0,5 |
0,005 |
|
24 |
24000 |
8,8 |
12 |
0,8 |
0,8 |
0,008 |
|
25 |
25000 |
9,2 |
12,9 |
0,4 |
0,9 |
0,0065 |
|
26 |
26000 |
10 |
13,2 |
0,8 |
0,3 |
0,0055 |
|
27 |
27000 |
10,5 |
14 |
0,5 |
0,8 |
0,0065 |
|
do = 9,7 [mm]
l0 = 100 [mm]
du = 6 [mm]
lu = 12,8 [mm]
Pm..= 36000 [N]
PH = 10000[N]
Pe= 26000[N]
Pu = 26000 [N]
P 0,05 = 14500 [N]
Przekrój początkowy
![]()
[mm2]
Przekrój końcowy
![]()
[mm2]
Granica proporcjonalności
![]()
[MPa]
Granica plastyczności
![]()
[MPa]
Umowna granica sprężystości
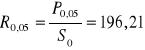
[MPa]
Wydłużenie względne
![]()
Przewężenie względne
![]()
Wytrzymałość na rozciąganie
![]()
[MPa]
Naprężenia rozrywające
![]()
[MPa]
Moduł Younga
![]()
[MPa]
Wnioski:
W wyniku przeprowadzonego ćwiczenia laboratoryjnego otrzymałem kilka wielkości, które cechują dany materiał. Wartości te możemy porównać z wartościami tablicowymi. Moduł Younga jest zbyt duży jak dla tego typu materiału z jakiego był wykonany pręt.
5

P
ΔL
PH
P0,.25
Pe
Pu
Pm
Wyszukiwarka