Dziś wykonamy zadania z zasady indukcji matematycznej i rekurencji. Na sam początek taka zasada. Mamy dane jakieś twierdzenie T(n) dla liczby naturalnej n. Aby zbadać indukcyjnośc tego twierdzenia należy kolejno:

1. Sprawdzić prawdziwość T(1), ewentualnie T(2)

2. Skorzystać z założenia indukcyjnego, czyli założyć, że T(n) jest prawdziwe dla wybranej liczby naturalnej n.

3. Udowodnić prawdziwość T(n+1) - jest to takzwany krok indukcyjny

4. Wywnioskować, że
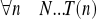
   jest prawdziwe.

I teraz na podstawie tego wykonajmy takie zadanie według powyższych czterech kroków. Należy udowodnić, że:

.

I tak:

1. Sprawdzamy dla n = 1:

L =

P =

Sprawdzamy dla n = 2:

L = 8

P =

2. Zakładamy, ze dla pewnego n naturalnego:

3. Udowodnijmy, że:

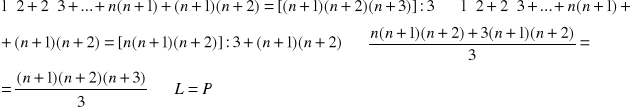
4.Dla każdego
:

Teraz praca domowa. Należy podobnie, jak powyżej udowodnić następujące twierdzenia:

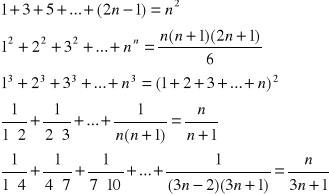
A my wykonajmy kolejne zadanie. Należy udowodnić, że T(n):
.

1. Sprawdzamy dla n = 1. Wówczas:

Sprawdzamy dla n = 2. Wówczas:

2. Zakładamy, że dla pewnego n naturalnego:

3. Udowodnimy, że
. Najpierw jednak, aby obliczyć (n + 1) do 7 potęgi,

należy skorzystać ze wzoru dwumianowego Newtona: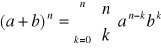
. Mamy więc za zadanie obliczyć: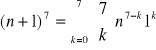
. Najpierw rozpisujemy na czynniki:

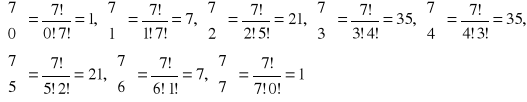
I teraz możemy dalej liczyć:

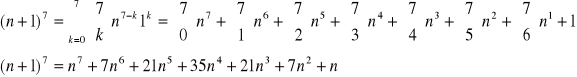
I tak:

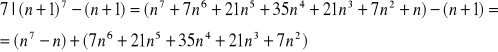
Z założenia
dzieli się przez 7 i drugi składnik też, więc całe wyrażenie dzieli się przez 7, co należało dowieść.

Na koniec takie cztery przykłady do domu z zasady indukcji matematycznej:

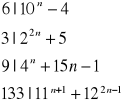
A teraz przejdziemy do rekurencji. I mamy takie zadanie. Przyjmijmy, że
. Oto, jak się bada rekurencję. Najpierw badamy trzy kolejne wyrazy:

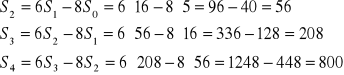
I tak dalej kolejne wyrazy. Przyjmijmy, że
. Wówczas:
. Stąd równanie charakterystyczne
.

Liczymy więc pierwiastki i deltę:
.

Wówczas:
, czyli:
, gdzie
wyznaczamy z warunku początkowego:

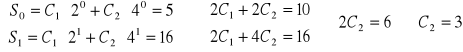
Stąd:
. Ostatecznie:
. I na koniec wykonajmy sprawdzenie:

I kilka przykładów do domu o tej samej tematyce:

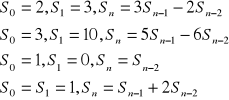
I na koniec zajęć zajmiemy się ciągiem Fibbonacciego. Przyjmijmy, że Fib(0) = Fib(1) = 1, oraz
Fib(n) = Fib(n-1) + Fib(n-2). Przyjmujemy, że
. Wówczas:

. Stąd przyrównując to do 0 mamy równanie charakterystyczne, z którego wyliczamy pierwiastki, deltę:
.

. Stąd:
. Uwzględniając warunki początkowe mamy układ równań, który rozwiążemy metodą wyznacznikową:

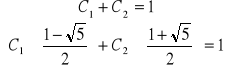
Wyznacznik W =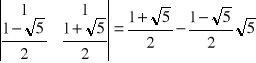
. Ponadto:

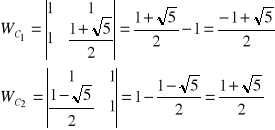
Stąd: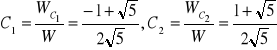

I ostatecznie: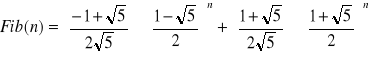

Nasze założenie

---