DECYZJE INWESTYCYJNE
Istota inwestycji
Inwestowanie jest to działalność gospodarcza o odroczonych efektach, mająca na celu poprawę efektywności działania, wzmocnienie pozycji rynkowej, poprawę wyników finansowych podmiotu gospodarczego.
Inwestycje wymagają wcześniejszego poniesienia wydatków, aby w późniejszym okresie uzyskać wpływy pieniężne.
Inwestycje mogą polegać na:
budowie nowych zdolności produkcyjnych, sprzedażowych
budowie sieci sprzedaży
modernizacji dysponowanych aktywów produkcyjnych
ponoszeniu wydatków na szkolenia pracowników
prowadzeniu kampanii reklamowej, promocyjnej
zakupie krótko- i długoterminowych papierów wartościowych
przejęciu innego przedsiębiorstwa
W ocenie projektu inwestycyjnego porównywane są ze sobą wydatki oraz wpływy powstałe dzięki inwestycji, co tworzy tzw. wielkość gotówki netto (CF)
CF = Wielkość gotówki netto = przepływ pieniężny netto, liczy się wg formuły:
zysk netto (zrealizowany dzięki inwestycji)
+ amortyzacja (tzw. koszty niepieniężne, które nie są wydatkiem)
= gotówka operacyjna
+/- inwestycje w aktywa trwałe (wydatki na modernizację lub sprzedaż akt. trwałych)
+/- inwestycje w aktywa obrotowe (wzrost lub spadek stanu zapasów i należności)
+/- zmiana stanu zobowiązań (wzrost lub spadek zobowiązań)
=gotówka netto
Kryteria oceny efektywności inwestycji
metody proste - nie uwzględniające przepływu pieniądza w czasie
wskaźnik rentowności PI
prosty okres zwrotu PP
księgowa stopa zwrotu ARR
metody złożone - uwzględniające przepływ pieniądza w czasie
wartość bieżąca netto NPV
wewnętrzna stopa zwrotu IRR
zdyskontowany okres zwrotu DPP
OCENA EFEKTYWNOŚCI INWESTYCJI
Wartość bieżąca netto NPV (Net Present Value)
Istota:
NPV mierzy nadwyżkę sumy zdyskontowanych wpływów nad sumą zdyskontowanych wydatków,
wpływy oraz wydatki realizowane w różnych okresach sprowadza się do porównywalności, dyskontując je na moment bazowy (w którym prowadzona jest analiza projektu inwestycyjnego, tzw. okres zerowy),
stopa dyskontowa oznacza:
wymaganą stopę zwrotu zależną od poziomu ryzyka prowadzonej
działalności gospodarczej,
koszt kapitałów finansujących projekt inwestycyjny.
Interpretacja:
NPV > 0. Stopa zwrotu jest wyższa niż koszt pozyskania kapitału. Przedsięwzięcie zwiększa zasoby firmy. Projekt kwalifikuje się do wstępnej akceptacji.
NPV = 0. Stopa zwrotu jest równa kosztowi pozyskania kapitału. Przedsięwzięcie nie zwiększa ani nie zmniejsza zasobów firmy. Projekt jest neutralny.
NPV < 0. Stopa zwrotu jest niższa niż koszt pozyskania kapitału. Przedsięwzięcie zmniejsza zasoby firmy. Projekt kwalifikuje się do odrzucenia.
Wzór
![]()
CFi = wielkość wolnej gotówki w i-tym okresie (przepływ pieniężny i-tego okresu)
I0 = początkowe wydatki inwestycyjne (przepływ pieniężny i=0)
r = stopa dyskontowa = koszt kapitału = wymagana stopa zwrotu
n = okres eksploatacji inwestycji.
Przykład. Wartość bieżąca netto NPV (Net Present Value)
Przykład A
Firma rozpatruje 3 letnią eksploatację projektu inwestycyjnego. Stopa dyskontowa właściwa dla projektu wynosi r=10%.
Polecenie: Obliczyć NPV projektu zakładając jednolitą stopę dyskonta.
Okres |
0 |
1 |
2 |
3 |
CFi |
-1000 |
200 |
700 |
900 |
r |
- |
10% |
10% |
10% |
![]()
Odp. Projekt inwestycyjny generuje dodatnią wartość NPV, dlatego też można go wstępnie zaakceptować.
Przykład B
Firma rozpatruje 3 letnią eksploatację projektu inwestycyjnego. Przewiduje się, że w przyszłości ryzyko prowadzonej działalności gospodarczej będzie się zmniejszało, stąd założono malejącą stopę dyskonta.
Polecenie: Obliczyć NPV projektu, zakładając zróżnicowaną stopę dyskonta.
Okres |
0 |
1 |
2 |
3 |
CFi |
-1000 |
200 |
700 |
900 |
r |
- |
12% |
10% |
8% |
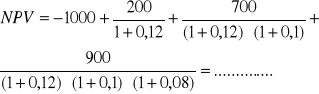
Odp. Projekt inwestycyjny generuje ………….wartość NPV, dlatego też …………………………………………………………………………………………
Wewnętrzna stopa zwrotu IRR (Internal Rate of Return)
Istota:
wraz ze wzrostem stopy dyskontowej r, NPV osiąga coraz to niższe wartości, w rezultacie dla pewnej krytycznej wartości stopy dyskonta, projekt jest neutralny, ponieważ nie zwiększa ani nie zmniejsza zasobów firmy,
IRR pokazuje krytyczną wartość stopy dyskontowej (IRR=r ) dla której wartość bieżąca netto (NPV) jest równa 0,
IRR można wyznaczyć przyrównując do 0 formułę NPV:
Wzór
![]()
Interpretacja:
r < IRR. Przy danym koszcie kapitału (r ) inwestycja generuje dodatnią wartość bieżącą netto. Przedsięwzięcie zwiększa zasoby firmy. Projekt kwalifikuje się do wstępnej akceptacji.
r = IRR. Koszt kapitału (r ) jest równy IRR, co oznacza, że przedsięwzięcie nie zwiększa ani nie zmniejsza zasobów firmy, jest neutralny.
r > IRR. Przy danym koszcie kapitału (r ) inwestycja pochłania środki finansowe, nie tworząc wystarczająco dużych wpływów. Projekt tworzy ujemną wartość bieżącą netto i należy go odrzucić.
Duże odchylenie (r < IRR) jest miarą bezpieczeństwa finansowego projektu inwestycyjnego i projekt charakteryzuje się względnie małą wrażliwością na zmiany kosztu kapitału. Oznacza margines bezpieczeństwa, tj. odpowiada na pytanie, w jakim stopniu może się zmieniać stopa dyskontowa, nie prowadząc do ujemnej wartości NPV.
Spełnienie warunku (r < IRR) nie powoduje ostatecznej akceptacji danego przedsięwzięcia, a oznacza przyjęcie go do dalszych rozważań.
Przykład. Wewnętrzna stopa zwrotu IRR (Internal Rate of Return)
Koszt kapitału (r) =10%
Wewnętrzna stopa zwrotu (IRR) = 28 %
Okres eksploatacji (n) =3 lata
Wartość IRR=28% oznacza, iż projekt w ciągu 3 lat zapewnia średnią roczną stopę zwrotu =28%, przy koszcie kapitału=10%. Stąd stopa dyskontowa (koszt kapitału) może wzrosnąć o 18 % (z 10% do 28%), nie prowadząc do ujemnej NPV.
Projekt ma duży margines bezpieczeństwa i jest mało wrażliwy na zmianę kosztu kapitału, stąd należy go uznać za bezpieczny.
3.1 Wskaźnik rentowności PI (Profitability Index)
Istota:
informuje o efektywności nakładów inwestycyjnych w stosunku do wpływów z inwestycji
pozwala na wybór projektu, który z jednostki nakładów (wydatków) daje największą wartość wpływów
uwzględnia wartość pieniądza w czasie, ponieważ wpływy i wydatki zostają zdyskontowane
Wzór
![]()
PV (wpływów) - suma zdyskontowanych wpływów z projektu inwestycyjnego (wartość bieżąca)
PV (wydatków) - suma zdyskontowanych wydatków z projektu inwestycyjnego (wartość bieżąca)
Interpretacja:
W przypadku, gdy mamy do czynienia z wariantami inwestycyjnymi o rożnych nakładach kapitałowych, NPV nie stanowi wystarczającej przesłanki wyboru konkretnego przedsięwzięcia, stąd wskaźnik PI jest lepszą miarą oceny.
Stosując to kryterium oceny inwestycji wybiera się projekt charakteryzujący się wyższym poziomem wskaźnika rentowności PI, ponieważ świadczy to o większych wpływach z jednostki poniesionych nakładów.
3.2 Przykłady. Wskaźnik rentowności PI (Profitability Index)
Firma rozpatruje 2 projekty inwestycyjne o następujących wolnych przepływach pieniężnych CFi (w zł). Obydwa projekty są eksploatowane w ciągu 1 roku oraz charakteryzują się takim samym poziomem ryzyka (r=10%)
Polecenie:
1. Który projekt jest korzystniejszy z punktu widzenia wskaźnika rentowności (PI).
2. Który projekt jest korzystniejszy z punktu widzenia nadwyżki finansowej netto (NPV).
Okres eksploatacji |
Projekt A CFi |
Projekt B CFi |
0 |
-100 |
-500 |
1 |
300 |
1000 |
Ad 1 Projekt A
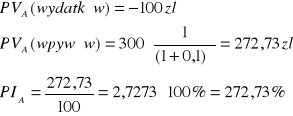
Projekt A pozwala zrealizować stopę zwrotu netto w wysokości 172,73%, (272,73%-100%) co oznacza, że 100 zł nakładów inwestycyjnych generuje 172,73 zł zdyskontowanych wpływów.
Ad 2 Projekt A
![]()
Jednocześnie projekt A pozwala zrealizować nadwyżkę finansową netto na poziomie 172,73 zł.
Ad 1 Projekt B
………………………………………………………………………………………
Ad 2 Projekt B
………………………………………………………………………………………
4.1. Księgowa stopa zwrotu ARR (Accounting Rate of Return)
Istota:
przeciętna stopa zwrotu z inwestycji z całego okresu eksploatacji obiektu
można ją wyznaczyć na 2 sposoby:
na podstawie zysków (Z) tworzonych przez obiekt powstały dzięki inwestycji
na podstawie wolnych środków gotówkowych (CFi), które generuje inwestycja
1) Wzór (uwzględniający zysk Z)
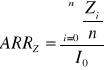
2) Wzór (uwzględniający przepływy pieniężne CFi)
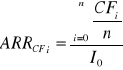
Z - zysk (strata) netto osiągany w i - tym okresie,
CFi - wolne środki pieniężne wygenerowane przez projekt w i-tym okresie,
n - liczba okresów eksploatacji obiektu,
I0 - początkowy wydatek inwestycyjny.
Interpretacja:
Przy wyborze wariantu inwestycyjnego należy się kierować maksymalizacją wskaźnika.
ARR jest prostym i użytecznym wskaźnikiem przy rozpatrywaniu projektów, jednak nie uwzględnia jednak wartości pieniądza w czasie, stąd powinien być stosowany pomocniczo.
4.2. Przykłady. Księgowa stopa zwrotu ARR
Obliczyć ARR dla obydwu projektów A i B z przykładu 3.2.
ARR (projekt A) ……………………………………………………………………
ARR (projekt B) ……………………………………………………………………
5.1. Prosty okres zwrotu PP (Playback Period)
Istota:
informuje o okresie, po którym następuje zrównanie wpływów z inwestycji z (wcześniej poniesionymi) wydatkami ,
nie uwzględnia wartość pieniądza w czasie, wpływy i wydatki nie zostają zdyskontowane
Interpretacja:
W przypadku, gdy mamy do czynienia z kilkoma wariantami inwestycyjnymi należy wybrać projekt, którego okres zwrotu jest krótszy (mniej ryzykowny).
Miara PP nie powinna być jedynym kryterium oceny inwestycji, ponieważ nie uwzględnia wartości projektu po okresie zwrotu (NPV) oraz poziomu efektywności nakładów (PI).
5.2 Przykłady. Prosty okres zwrotu PP
Firma rozpatruje 2 projekty inwestycyjne o następujących wolnych przepływach pieniężnych CFi (w zł). Obydwa projekty są eksploatowane w ciągu 3 lat.
Polecenie:
1. Po jakim okresie zwrócą się nakłady inwestycyjne dla obydwu projektów.
2. Który projekt jest korzystniejszy z punktu widzenia miary PP?
Okres eksploatacji |
Projekt A CFi |
Projekt B CFi |
0 |
-1000 |
-1000 |
1 |
200 |
900 |
2 |
700 |
700 |
3 |
900 |
200 |
Rozwiązanie
Okres eksploatacji |
Projekt A CFi |
Skumulowana gotówka netto |
Projekt B CFi |
Skumulowana gotówka netto |
0 |
-1000 |
-1000 |
-1000 |
|
1 |
200 |
-800 |
900 |
|
2 |
700 |
-100 |
700 |
|
3 |
900 |
800 |
200 |
|
![]()
Dla projektu A tworzenie nadwyżki finansowej rozpoczyna się po upływie………
Dla projektu B………………………………………………………………………
6.1. Zdyskontowany okres zwrotu DPP (Discounted Playback Period)
Istota:
informuje o okresie, po którym następuje zrównanie bieżącej wartości wpływów z inwestycji z wartością bieżącą wydatków,
uwzględnia wartość pieniądza w czasie, wpływy i wydatki zostają zdyskontowane
Interpretacja:
W przypadku, gdy mamy czynienia z kilkoma wariantami inwestycyjnymi należy wybrać projekt, którego okres zwrotu jest krótszy (mniej ryzykowny).
6.2 Przykłady. Zdyskontowany okres zwrotu DPP
Firma rozpatruje 2 projekty inwestycyjne o następujących wolnych przepływach pieniężnych CFi (w zł). Obydwa projekty są eksploatowane w ciągu 3 lat. Stopa dyskonta r=10%.
Polecenie:
1. Po jakim okresie zwrócą się nakłady inwestycyjne dla obydwu projektów.
2. Który projekt jest korzystniejszy z punktu widzenia miary DPP?
Okres eksploatacji |
Projekt A CFi |
Projekt B CFi |
0 |
-1000 |
-1000 |
1 |
200 |
900 |
2 |
700 |
700 |
3 |
900 |
200 |
Rozwiązanie
Okres eksploatacji |
Zdyskontowana gotówka netto dla projektu A |
Zdyskontowana skumulowana gotówka netto dla projektu A |
Zdyskontowana gotówka netto dla projektu B |
Zdyskontowana skumulowana gotówka netto dla projektu B |
0 |
-1000 |
-1000 |
|
|
1 |
181,82 |
-818,18 |
|
|
2 |
578,51 |
-239,67 |
|
|
3 |
676,18 |
436,51 |
|
|
![]()
Zdyskontowany okres zwrotu jest dłuższy od prostego okresu zwrotu i kształtuje się na poziomie ……... lat i ……. dni.
Dla projektu B………………………………………………………………………
1
1
Wyszukiwarka