CZŁON CAŁKUJĄCY IDEALNY

(wykonuje operację odwrotną) :

.

Równanie różniczkowe WE - WY: y = ku

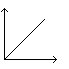
K - współczynnik wzmocnienia prędkościowego, określany jako stosunek pochodnej odpowiedzi y do wymuszenia u w czasie ustalonym.

Charakterystyka skokowa (stała): h(t) = k t 1(t)

Odpowiedź impulsowa (pochodna): g(t) = k 1(t)

K

Transmitacja: g(`s) =

S'

Przykłady:

ZBIORNIK Z CIECZĄ

We - objętość cieczy dopływająca jednostce czasu ( g(t) )

Wy - poziom cieczy

G(t) d V(t)

G(t) =

dt

str. dopływający Szybkość narastania

objętości

wys. Słupa wody: h(t) * S = V(t)

d h(t)

S = g(t)

dt

_t

h(t) = 1/s ∫ g(t) dt

⁰

2. Kondensator idealny.

3. Układ napędowy pozycyjny.

CZŁON CAŁKUJĄCY Z INRCJĄ

.. .

Równanie różniczkowe WE - WY: Ty + y = ku

K - współczynnik wzmocnienia prędkościowego określany jako stosunek pochodnej odpowiedzi y do wymuszenia u w stanie ustalonym

T - stała czasowa

Charakterystyka skokowa:

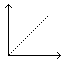
t

h(t) = (kt - kT ( 1-exp [- ] ) ) 1(t) układ będzie dążył do całki

idealnej.

T

Odpowiedź impulsowa:

t

h(t) = k [ 1-exp [- ] ] 1(t)

T

K

Transmitacja: g(s) =

S(1+sT)

Przykłady:

1. OBCOWZBUDNY SILNIK PRĄDU STAŁEGO

Założenia: silnik nieobciążony, uwzględniamy tylko bezwładność

We - napięcie twornika

Wy - kąt położenia wału silnika

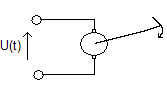
Ω(t) (WY - położenie kątowe)

α(t)

Ø - strumień jednego z uzwojeń

Const

DI(t)

U(t) = R_t * I(t) + L_t E(t)

dt

pomijam(małe)

dΩ(t)

M_n(t) - M_z(t) = I M_n(t) = C_m * Ø * I(t)

dt

Chcemy powiązać 2 wielkości: α(t) i U(t)

d α(t)

= Ω(t) No i manipulujemy, aby była zależność α(t) do U(t)

dt

dΩ(t)

C_m Ø Ω(t) * I(t) = J

dt

U(t) = R_t * I(t) + C_E Ø Ω(t)

J dΩ(t)

I(t) = *

C_M Ø dt

R_t * J d² α dα

U(t) = * + C_EØ

C_mØ dt² dt

CZŁON INERCYJNY II RZĘDU

Równanie różniczkowe: T₁T₂y'' + T₁y_t' + y = ku

Lub

T_AT_By'' + (T_A+T_B) y' + y = ku

K - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym.

T₁T₂T_AT_B - stałe czasowe.

K

Transmitacja: G(s) =

T₁T₂S² + T₁S + 1

Lub

K

G(s) =

T_AT_BS² + (T_AT_B) s + 1

T₁ - 4T₂ >=0 __

____ 1 √T₁

T_{B =} √T₁T₂ , S = __

2 √T₂

_____ T_A + T_B

T₀ = √T_AT_B , ζ = _____ , K = K_A - K_B

2 √T_AT_B

K_A

G₁(s) =

1 + STA

K_B

G₂(s) =

1 + STB

Przykład:

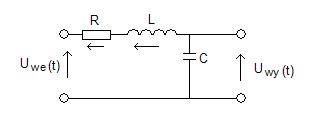
CZWÓRNIK R,C,

dI(t) 1 _t

U_we(t) = R * I(t) + L + ∫ I(t)dt

dt c ⁰

1 _t dU_wy

U_wy(t) = ∫ I(t) dt c = I(t) różniczkuje raz jeszcze

C ⁰ dt

dU_wy d²U_wy d²U_wy dI

U_we(t) = RC * + L C + U_wy C = =

dt dt dt dt

To czy układ będzie inercyjny II rzędu, czy oscylacyjny zależy od parametrów

CZŁON OPÓŹNIAJĄCY

Równanie różniczkowe: y(t) = ku( t - T₀)

K - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u dla

t >T₀

T₀ - czas opóźnienia

Charakterystyka skokowa: h(t) = k 1(t - T₀)

Odpowiedź impulsowa: g(t) = kδ(t - T₀)

Transmitacja: g(s) = ex (-sT₀)

CZŁON OSCYLACYJNY

Odpowiada na wymuszenie

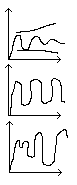
1. Tłumione

2.Nie Tłumione

3. Narastanie.

TRANSMITACJA OPERATOROWA:

Transformata Laplace'a: _∞

F(s) = ∫ f(s) e^-st = L[ f(t) ]

⁰

Orginały Laplace'owskie ( f(t) będzie orginałem, jak spełni 3 warunki):

1. f(t) = 0 t<0 Obserwacje prowadzimy w przód, nie bierzemy pod uwagę

przeszłości.

2. Funkcja ciągła i monotoniczna przedziałami.

3. f(t) <= m* e ^αt Można zrobić na funkcjach , które rosną, ale nie szybciej jak funkcja wykładnicza( np. e^t)2 nie da się jej ograniczyć);

Własności transformaty Laplace'a:

1. Złożenie dwóch operacji

L^-1[L(f(t))] - f(t) , L[L^-1(F(s))] = F(s)

α(1(t)) = 1/s , α^-1(1/s) = 1(t)

1 1

L( e^-αt * 1(t)) = , L^-1 ( ) = e^-αt * 1(t)

S+α S+α

Funkcje określam dla czasu T = 0

2. Liniowość:

Obowiązuje zasada superpozycji( odpowiedź na wymuszenie jest odpowiedzią na sumę tych wymuszeń.

L [a₁f₁(t) + a₂f₂(t)] = a₁L[f₁(t)] + a₂L[f₂(t)]

Przykłady:

( e^jωt = cos ωt + j sin ωt)

( e^-jωt = cos ω - j sin ωt)

1

sin ωt = ( e^jωt - e^-jωt)

2j

1 1 1 1 2jω ω

L { sin ωt * 1(t) } = ( - ) = * =

2j s-jω s+jω 2j s² + ω² s² + ω²

ω

L { sin ωt } =

s² + ω²

4

sin 4t =

s² + 16

1 3

L^-1 ( ) = L^-1 ( ⅓ * ) = ⅓* sin 3t

s² + 9 s² + 9

3. Holomorficzność (funkcja, która ma pochodne):

dF(s) dF(s)

= -∫ t f(t) e^-st dt czyli L[t f(t)] = -

ds. ds.

oraz

n! n!

L(fⁿ) = , L(ten^-αt) =

Sⁿ⁺¹ (s + α)ⁿ⁺¹

L { t*1(t)} = 1/s

-1 1

- =

s² s²

s+2 1 3 1 1 1 3 1

L^-1 ( = L^-1 (-2 * + * + * ) = (-2 + e^t+ e^-t)1(t)

s(s² - 1) s 2 s-1 2 s+1 2 2

3. Transformata pochodnej:

ω s

L (cos ωt) = L (1/ω(sin ωt)') = 1/ω *(s*L(sin ωt) - sin 0 ) = 1/ω * s * =

s² + ω² s²+ω²

Idea rachunku operatorowego

Mamy problem w dziedzinie czasu

Równanie L równanie wyznaczanie L wyznacznie

Dla orginału dla obrazu obrazu oryginału

Przykład: dI(t)

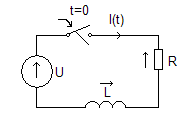
U *1(t) = R*I(t) + L

dt

równanie obrazu bo oper, różniczkowemu

odpow. mnożenie przez s.

*U1/s = R * I(s) + L*s*I(t)

u 1

I(s) = *

S R*SL

Rozw w dziedzinie Laplace'a

Faza końcowa - wyznaczenie oryginału.

1 K/R U/R

= 1/s + = -

s+R/L S s + R/L

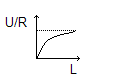
I(t) = U/R * (1 - e^-(R/L)*t) * 1(t)

pisane

CZŁON RÓŻNICZKUJĄCY

.

Równanie różniczkujące WE/WY: y = ku

K - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do pochodnej wymuszenia w stanie ustalonym

T - stała czasowa = 0

Charakterystyka skokowa: h(t) = uδ(t)

dδ(t)

Odpowiedź impulsowa: g(t) = k (pochodna z odpowiedzi skokowej)

dt

Transmitacja: g(s) = ks

Przykład:

(nie ma idealnych członów różniczkujących)

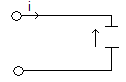
dU(t)

KONDENSATOR i(t) = c

dt

Uc(t) = 1/c ∫ i(t) dt

CZŁON RÓŻNICZKUJĄCY Z INERCJĄ

(rzeczywisty człon różniczkujący)

. .

Równanie różniczkujące WE-WY: Ty + y = ku

K - współczynnik wzmocnienia określany jako odpowiedź y do pochodnej wymuszenia u w stanie ustalonym

T - stała czasowa

k 1

Charakterystyka skokowa: h(t)= exp ( - ) 1(t)

T T

Odpowiedź impulsowa: k k 1

g(t)= δ(t) - exp( - ) 1(t)

T T² T

ks

Transmitacja: g(s) =

1+sT

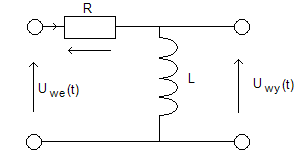
Przykład:

CZWÓRNIK R,L d I(t)

U_we(t) = R * I(t) + L =

dt

= R I(t) + U_wy(t)

dI(t)

U_wy(t) = L

dt

d U_we(t) d I(t) d U_wy(t)

= R +

dt dt dt

Równanie końcowe:

d U_we R d U_wy . _.

= * U_wy(t) + => u = k * y + y

dt L dt

Przykład **:

TRANSFORMATOR :

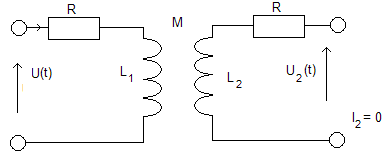
d I₁

U₁ = RI₁ + L₁

dt .

I

d I₁

U₂ = M

dt

. . ..

U₁ = R₁ I₁ + L₁ I

. R L₁ .

U₁ = U₂ + U₂ / M/R

M M

M . L₁ .

U₁ = U₂ + U₂

R R₁

K T

---