TEMAT: BADANIE SKRĘCANIA PŁASZCZYZNY POLARYZACJI ŚWIATŁA.

1. Cel ćwiczenia

Naszym zadaniem na laboratorium było zbadanie zjawiska skręcenia płaszczyzny polaryzacji światła. Badaliśmy związek kąta skręcenia od stężenia roztworu. Ćwiczenie wykonywaliśmy dla wody destylowanej oraz dla kilku wartości stężenia cukru w wodzie. W drugiej części badaliśmy zjawisko Faraday`a oraz wyznaczaliśmy stałą Verdeta V.

2. Wprowadzenie teoretyczne

W zjawisku polaryzacji światło zachowuje się jak fala elektromagnetyczna, czyli rozchodzący się w przestrzeni ciąg zmiennych pól elektrycznych i magnetycznych wzajemnie się wytwarzających. Opisana jest za pomocą trzech wektorów: E - wektora natężenia pola elektrycznego, B - wektora natężenia pola magnetycznego oraz wektora określającego kierunek rozchodzenia się fali k.

Kiedy wektor E zmienia swój kierunek dowolnie wtedy taką falę nazywamy niespolaryzowaną. Można jednak doprowadzić do tego, aby światło było spolaryzowane liniowo. Polaryzacja liniowa ma miejsce, gdy drgania wektora natężenia pola elektrycznego zachodzą tylko w jednej

płaszczyźnie, która nie zmienia w czasie swej orientacji w przestrzeni.

Światło spolaryzowane możemy otrzymać poprzez użycie polaryzatorów dwójłomnych, polaryzatorów odbiciowych lub polaroidów, czyli błon polaryzujących. Polaroidem może być np. przezroczysta błona z alkoholu poliwinylowego, rozciągniętego a następnie zanurzonego w roztworze bogatym w jod. Fale, które padają równolegle na takie błony są pochłaniane natomiast te które padają prostopadle przechodzą przez nią. Polaryzację uzyskujemy także poprzez odbicie od dielektryka. Promień odbity zostaje całkowicie spolaryzowany tylko wtedy, gdy jest prostopadły do promienia załamanego.

Jeszcze innym sposobem jest użycie kryształów dwójłomnych, czyli takich, które rozdzielają padającą wiązkę na dwie załamane zwane zwyczajną i nadzwyczajną. Wiązka nadzwyczajna jest spolaryzowana liniowo. Najbardziej znanym polaryzatorem dwójłomnym jest pryzmat Nicola składający się z dwóch sklejonych połówek kryształu kwarcu.

Oprócz właściwości dwójłomności, niektóre kryształy posiadają także inną właściwość- mają zdolność skręcania fali świetlnej. Mówimy o nich wtedy, że są to ciała aktywne optycznie. Takie właściwości posiadają również ciecze, np. badany w czasie laboratorium roztwór cukru w wodzie. Kąt skręcenia płaszczyzny polaryzacji badaliśmy za pomocą polarymetru półcieniowego. Korzystając z zależności:

α= h c γ

gdzie:

c - gęstość cieczy

h - długość drogi optycznej jaką musi pokonać fala przez daną substancję

γ - współcznynnik skręcenia właściwego.

obliczaliśmy współczynnik skręcenia właściwego.

Zjawisko aktywności optycznej może też być wymuszone niektórymi czynnikami

fizycznymi jak np. polem magnetycznym. Ciała, które w nieobecności pola magnetycznego nie są aktywne optycznie, po umieszczeniu w polu magnetycznym skręcają płaszczyznę polaryzacji. Zjawisko to zostało odkryte przez Faraday`a.

Kąt skręcenia polaryzacji w zjawisku Faraday`a opisany jest wzorem (dla fali posiadający kierunek równoległej do kierunku wektora indukcji magnetycznej B)

gdzie V jest współczynnikiem proporcjonalności zwanym stałą Verdeta.

Wyznaczenie tego współczynnika było naszym zadaniem w części drugiej ćwiczenia.

3. Przebieg ćwiczenia

Na początku ustawiliśmy kąt zerowy dla kuwety napełnionej wodą destylowaną., w stosunku do którego liczyliśmy skręcenie płaszczyzny polaryzacji dla roztworów cukru w wodzie. Odmierzyliśmy następujące ilości cukru: 1g, 2g, 4g, 6g, 8, 10g. Dla każdej ilości sprawdzaliśmy wartość kąta skręcenia płaszczyzny polaryzacji i liczyliśmy różnicę pomiędzy kątem zerowym. Wyniki znajdują się w poniższej tabeli:

=172,3° - kąt początkowy dla kuwety z wodą destylowaną

Długość kuwety z badaną substancją wynosi: h = 154 ± 0,5 [mm];

Nr	Stężenie roztworu cukru	Wartości kątów	Wartości kątów
1.	0,0196	174,05^O	1,75^O
2.	0,0385	175,3^O	3^O
3.	0,0741	179,6^O	7,3^O
4.	0,1071	182,5^O	10,2^O
5.	0,1379	187,7^O	15,4^O
6.	0,1667	190,5^O	18,2^O

Metodą najmniejszej sumy kwadratów, korzystając z zależności α= h c γ

gdzie x=stężenie, y=kąt skręcenia, wyznaczyliśmy współczynnik a=
(h - grubość warstwy roztworu, γ - współczynnik skręcenia właściwego) oraz błąd współczynnika ∆a za pomocą programu Origin.

[
]

Przyjmując współczynnik studenta dla β=0,95 otrzymujemy

Błąd wielkości γ policzymy z różniczki zupłnej:

=0,09716

ODP: γ=0,737±0,098 [
]

II cześć:

Drugim naszym zadaniem było zbadanie jak zależy kąt α skręcenia płaszczyzny polaryzacji od natężenia prądu I. Przy różnych wartościach natężenia

( od 1..6 [A]) odczytywaliśmy kąt skręcenia płaszczyzny polaryzacji światła na polarymetrze. Korzystając z zależności
liczymy wartość indukcji magnetycznej. Wyniki znajdują się w poniższej tabeli:

Lp	I [A]	α[º]	α[rad]	[T]	[º]	[rad]	[º]	[rad]
1.	1	110,1	1,92108	0,01718	107,1	1,86925	3	0,05236
2.	2	113,2	1,97571	0,03437	107,1	1,86925	6,1	0,10647
3.	3	115,8	2,02109	0,05155	107,1	1,86925	8,7	0,15184
4.	4	118,2	2,06298	0,0687	107,1	1,86925	11,1	0,19373
5.	5	120,8	2,10836	0,08588	107,1	1,86925	13,7	0,23911
6.	6	123,5	2,15548	0,1031	107,1	1,86925	16,4	0,28623

Korzystając z programu Origin metodą najmniejszej sumy kwadratów liczymy z równania

gdzie x=B, y=α współczynnik kierunkowy a=Vh oraz błąd współczynnika ∆a.

Współczynnik kierunkowy (odczytany z wykresu):

a=2,67624

błąd współczynnika „a” wynosi( po uwzględnieniu współczynnika studenta:

Ostatecznie stała Verdeta:

błąd zaś:

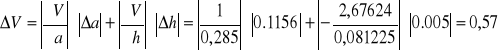
ODP:

IV.Wnioski

Otrzymana zależność kąta skręcenia płaszczyzny polaryzacji od stężenia roztworu cukru w wodzie dla pierwszej części ćwiczenia jest zależnością liniową. Niewielkie odchylenia punktów od prostej świadczą o niewielkim błędzie wykonania ćwiczenia (mogło to być spowodowane błędnym odczytaniem na analizatorze np. z powodu zabrudzeń na kuwecie lub niedokładnym odmierzeniu odpowiedniej ilości cukru na wadze).

W drugiej części ćwiczenia mieliśmy wyznaczyć zależność kąta skręcenia płaszczyzny polaryzacji w funkcji indukcji magnetycznej B wytwarzanej przez różne wartości natężenia prądu I. Ta zależność również okazała się liniowa a otrzymany wynik charakteryzuje się stosunkowo niskim błędem.

---