EKONOMETRIA - WYKŁADY.
Wykład z dnia 9.03.2012 r.
Funkcja regresji.
Narzędziem badania mechanizmu powiązanego między zmiennymi jest funkcja regresji.
Funkcja regresji to analityczny wyraz podporządkowujący średnią zmiennych objaśnianych konkretnych wartości zmiennych objaśniających
Daje to funkcji 1 -ego rodzaju realizację zmiennych objaśniających, przypisuje średnie warunkowe zmiennej objaśnianej.
Jeżeli badanie statystyczne dotyczy dwóch zmiennych to funkcja regresji 1 - pierwszego rodzaju zmiennych losowych y względem zmiennych losowych x nazywamy:
![]()
( pierwszy wzór)
Gdzie:
![]()
to jest wartość losowa y pod warunkiem że x = xi
Analiza funkcji regresji 1 - ego rodzaju zmiennych x względem y nazywamy średnią warunkową zmiennej x, która jest funkcją ustalonych wartości ![]()
(drugi wzór).
Analityczne postacie funkcji xy i qi są nieznane. Dlatego na podstawie zaobserwowano wyniki w próbie tego rodzaju powiązania, przedstawiają się następująco:
W prostokątny układ współrzędnych w formie empirycznej linii regresji.
Empiryczna linia regresji zmiennej x względem y jest linią łamaną powstałą przez połączenie punktu o współrzędnych :![]()
empiryczną linią regresji y względem x jest linią łamaną powstała przez połączenie punktu ![]()
Przykładowe zadanie.
Chcemy w badaniu zależności między wiekiem kobiet, a liczbą posiadanych dzieci. W sposób niezależny wylosowano :
Wiek dzieci v |
Wiek kobiet |
|||
|
25-25 |
25-35 |
35-45 |
45-55 |
0 |
2 |
1 |
- |
- |
1 |
10 |
12 |
15 |
- |
2 |
8 |
19 |
10 |
5 |
3 |
- |
- |
5 |
4 |
4 |
- |
- |
- |
3 |
5 |
- |
- |
- |
6 |
Na podstawie danych sporządź, wykres empirycznych linii regresji w celu określenia średnich warunkowych obydwu zmiennych x przy ustalaniu wartości zmiennej y który jest równy.
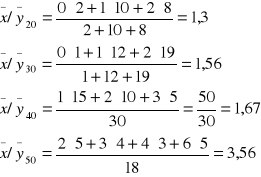
![]()
pod warunkiem że 0 dzieci
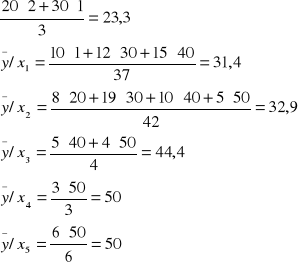
Zad. Przykładowe 2
Mamy tabelkę zależności inwestycji firmy od dochodu
x/y |
1 |
2 |
3 |
4 |
5 |
1 |
1 |
2 |
- |
- |
- |
2 |
2 |
3 |
1 |
- |
- |
3 |
1 |
2 |
2 |
1 |
- |
4 |
- |
- |
3 |
1 |
1 |
n = 17
x - inwestycje
y - dochód
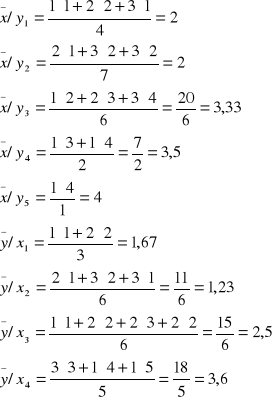
Funkcje regresji II rodzaju.
Ona jest aproksymantą czyli przybliżeniem funkcji regresji 1 - ego rodzaju opisującą zależność korelacyjną zmiennych w próbie losowej.
Wymóg analityczny postaci funkcji regresji II -ego rodzaju nie jest łatwy.
Zajmiemy się metodą badań zależności między dwiema zmiennymi, które mają postać liniową, w takich przypadkach regresja I - ego rodzaju opisującą zależność zmiennych losowych y od x, przyjmuje nastepującą postać:
![]()
(pierwszy wzór)
Gdzie:
Y - teoretyczne wartości funkcji regresji odpowiadającej danym poziomom realizacji zmiennej x
![]()
- parametry strukturalne liniowej funkcji regresji y względem x
![]()
- składnik losowy.
Natomiast liniowa funkcja regresji drugiej zmiennej x względem y ma postać:
![]()
(drugi wzór)
Występującą w równaniach regresji 1 - ego, 2 - ego rodzaju, składniki losowe pełnią rolę błędu przypadkowego zakrócającego funkcyjny związek między wartością zmiennych objaśnianych a wartością zmiennej objaśniającej.
Potrzeby wprowadzone składników losowych do modelu uzasadnia się następującymi względami:
a - w modelu nie jesteśmy w stanie uwzględnić wszystkich zmiennych objaśniających
b - przyjęto analityczną postać funkcji regresji niż odpowiada dokładnie rzeczywistej formie zależności między badanymi zmiennymi. Zwykle przyjmuje się że wartości mają wartości oczekiwania:
![]()
niewielkie
Oszacowanie funkcji regresji i1 zmiennej y względem w próbie losowej jest funkcja postaci :
![]()
(trzeci wzór)
Gdzie:
i = 1,2…n - tj. kolejne numery jednostek z populacji generalnej do próby ![]()
analogicznie oszacowanie funkcji regresji drugiej zmiennej x względem y jest funkcja regresji x względem y w próbie losowej postaci:
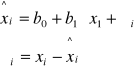
(czwarty wzór)
Funkcje regresji (trzeci i czwarty wzór) są dobrymi aproksymantami funkcji regresji 1 - ego rodzaju jeżeli spełnione są dwa warunki:
a - odchylenia wartości empirycznych Yi od wartości teoretycznych Yi są pochodzenia losowego tzn. są statystycznie nie istotne.
b - suma kwadratu odchyleń wartości empirycznych od teoretycznych stanowi minimum.
Problem losowości odchyleń może być zbadany po oszacowaniu parametrów strukturalnych danej funkcji regresji. Warunek b zaś jest spełniony jeżeli do szacowania paramteru funkcji regresji wykorzystano metody najmniejszych kwadratów.
![]()
Metoda najmniejszych kwadratów polega na takim oszacowaniu parametru a0 , a1 funkcji 3 (trzeci wzór), aby dla danych z próby n wartości
![]()
(czwarty wzór)
![]()
(piąty wzór)
Wyrażenie nr 5 jest funkcja dwóch zmiennych a0 , a1 . Zagadnienie sprowadza się do znalezienia minimum funkcji kwadratowej dwóch zmiennych a0 , a1 .
Warunkiem koniecznym istnienia ekstremum jest zerowanie się pochodnych cząstkowych ze względu na:
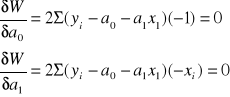
(szósty wzór)
Po odpowiednich przekształceniach w układzie równań 6 otrzymujemy:
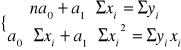
(wzór siódmy)
Układy równań 7 ma rozwiązanie:
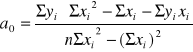
![]()
(wzór 8)
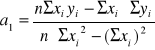
(wzór 9 )
Wzory 8 i 9 można przedstawić w prostszej postaci:
![]()
(wzór 10)
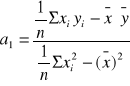
(wzór 11)
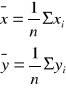
Postępując analogicznie w przypadku liniowej funkcji regresji x względem y otrzymamy następujące wzory na estygmatory b0 i b1.
Wzór 12
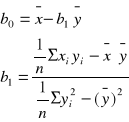
wzór 13
Zad. Przykładowe
W urzędzie stanu cywilnego przeprowadzono badanie nowo zawartych małżeństw według wieku męża i żony w jednym dniu.
W wieku żony - x
W wieku męża - y
X |
18 |
19 |
20 |
21 |
23 |
24 |
26 |
27 |
27 |
30 |
y |
19 |
21 |
23 |
21 |
20 |
23 |
26 |
25 |
26 |
34 |
n = 10
Znaleźć liniową funkcję regresji x względem y

Wyszukiwarka